文中所講的數(shù)字簽名技術(shù),就是我們在密碼學(xué)中保證身份同一性所用到的最重要的工具。身份同一性的意思即是,如何證明某條消息就是“我”發(fā)出的,別人不能偽造,我也不能抵賴。雖然數(shù)字簽名技術(shù)也會用到成對的密鑰對,但與我們所說的公鑰密碼學(xué)重點卻有所不同。(2)可以將本文視為思考密碼學(xué)工具的一個教程或者范本,能耐心讀下去,也就明白了密碼學(xué)是怎么樣一回事、我們在密碼學(xué)中是如何思考的。
回首近幾年,我有幸經(jīng)歷了兩個相互沖突、卻又令人著迷的時代潮流變遷。第一個潮流變遷是:專家學(xué)者們耗費四十年設(shè)計的密碼學(xué),終于派上用場;從信息加密、電話安全、到加密數(shù)字貨幣,我們可以在生活的方方面面發(fā)現(xiàn)使用密碼學(xué)的例子。
第二個潮流變遷是:所有密碼學(xué)家已經(jīng)做好準備,迎接以上美好的幻滅。
正文開始之前我得重申一下,本文所講的不是所謂量子計算啟示錄(末日預(yù)言),也不是要講 21 世紀密碼學(xué)的成功。我們要談?wù)摰氖橇硪患闯啥ň值氖虑椤艽a學(xué)有史以來最簡單的(也是最酷炫的)技術(shù)之一:基于散列函數(shù)的簽名。
在 20 世紀 70 年代末,Leslie Lamport 發(fā)明了基于哈希函數(shù)(Hash Function,又稱散列函數(shù))的簽名 ,并經(jīng)過 Ralph Merkle 等人進一步改進。而后的很多年,這被視為密碼學(xué)領(lǐng)域一灘有趣的“死水”,因為除了相應(yīng)地產(chǎn)生冗長的(對比其他復(fù)雜方案)簽名,基于哈希函數(shù)的簽名好像沒有什么作用。然而近幾年來,這項技術(shù)似乎有了復(fù)蘇的跡象。這很大程度歸因于它的特性——不同于其他基于RSA或離散對數(shù)假設(shè)的簽名,哈希函數(shù)簽名被視為可以抵抗量子計算攻擊(如 Shor‘s 算法)。
首先,我們進行一些背景介紹。
背景:哈希函數(shù)和簽名方法
在正式介紹哈希函數(shù)簽名之前,首先你得知道密碼學(xué)中的哈希函數(shù)是什么。哈希函數(shù)可以接受一串字符(任意長度)作為輸入,經(jīng)過“消化”后,產(chǎn)生固定長度的輸出。常見的密碼學(xué)哈希運算,像是 SHA2、SHA3 或 Blake2 等,經(jīng)運算會產(chǎn)生長度介于 256 ~ 512 位的輸出。
一個函數(shù) H(。) 要被稱作“密碼學(xué)”哈希函數(shù),必須滿足一些安全性的要求。這些要求有很多,不過我們主要聚焦在以下三個方面:
抗-原像攻擊 Pre-image resistance (或俗稱“單向性”):給定輸出 Y=H(X),想要找到對應(yīng)的輸入 X 使得 H(X)=Y 是一件“極度費時”的工作。(這里當(dāng)然存在許多例外,但最棒的部分在于,不論 X 屬于什么分布,找到 X 的時間成本和暴力搜尋相同。)
抗-次原像攻擊:這和前者有些微的差別。給定輸入 X,對于攻擊者來說,要找到另一個 X’ 使得 H(X)=H(X‘) 是非常困難的。
抗-碰撞:很難找到兩個輸入 X1, X2,使得 H(X1)=H(X2)。要注意的是,這個假設(shè)的條件比 抗-次原像攻擊還要嚴苛。因為攻擊者可以從無垠的選擇中尋找任意兩個輸入。
我們相信所有本文提到的哈希函數(shù)示例都能提供上述的所有特性。換言之,沒有任何可行的(甚至是概念上的)方法能破解它。當(dāng)然這種情況也是會變的,如果破解的方法被找到,我們當(dāng)然會立即停用哈希函數(shù)(稍后會討論關(guān)于量子計算攻擊的特例)。
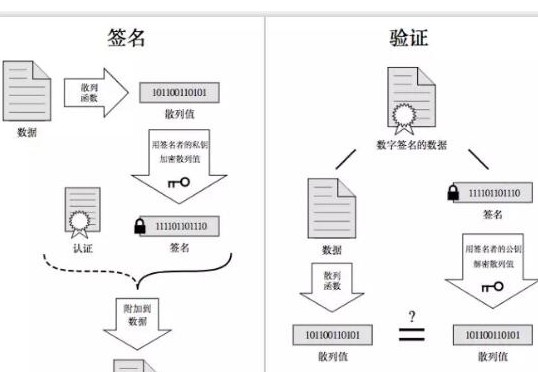
我們的目標(biāo)是使用哈希函數(shù)構(gòu)造數(shù)字簽名方案,因此簡要回顧數(shù)字簽名這個詞能帶來很大的幫助。
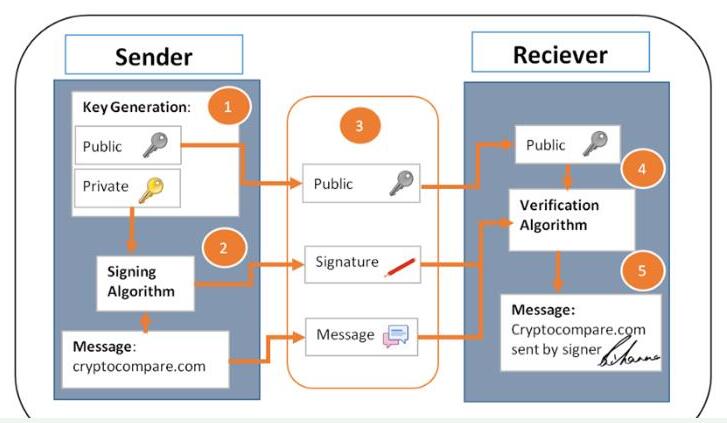
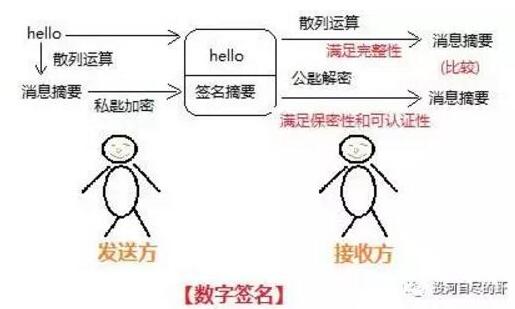
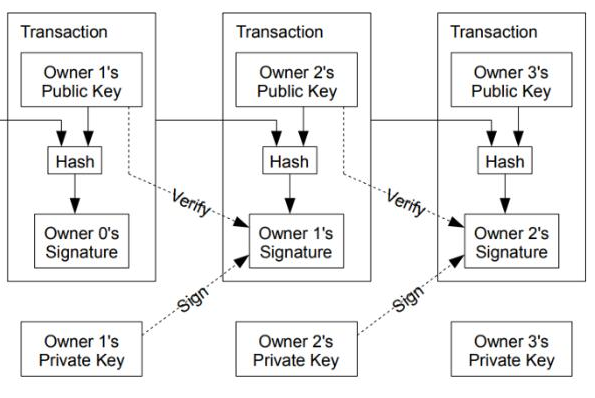
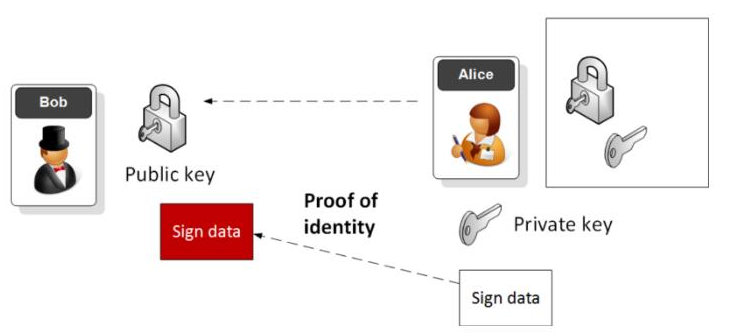
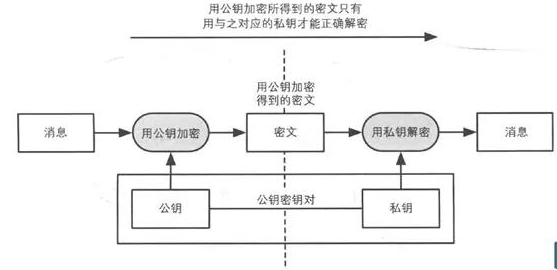
數(shù)字簽名方法源于公鑰的使用,使用者(簽署人)生成一對密鑰:公鑰和私鑰。使用者自行保管私鑰,并能夠用私鑰“簽署”任何消息,從而產(chǎn)生相應(yīng)的數(shù)字簽名。任何一個持有公鑰的人都能驗證該消息正確性和相關(guān)簽名。
從安全的角度來說,我們希望簽名是不可偽造的,或是說“存在不可偽造性”。這意味著攻擊者(沒有私鑰控制權(quán)的人)無法在某段消息上偽造你的簽名。
Lamport 一次性簽名
在 1979 年,一位名叫 Leslie Lamport 的數(shù)學(xué)家發(fā)明了世界上第一個基于哈希函數(shù)的簽名。Lamport 發(fā)現(xiàn)只要使用簡單的哈希函數(shù),或是單向函數(shù),就可以構(gòu)建出非常強大的數(shù)字簽名方法。
強大的前提是,用戶只需要做一次簽名的動作就能保證安全性!后續(xù)會做更詳細的闡述。
為了更好的討論,我們假設(shè)以下條件:一個哈希函數(shù),它能接受 256 位的輸入并產(chǎn)生 256 位的輸出; SHA256 哈希函數(shù)就是個絕佳的示范工具;我們也需要能產(chǎn)生隨機輸入的方法。
假設(shè)我們的目標(biāo)是對 256 位的消息進行簽名。要得到我們需要的密鑰,首先需要生成隨機的 512 個位字符串,每個位字符串長度為 256 位。為了便于理解,我們將這些字串列為兩個獨立的表,并以符號代指:
sk0= sk10, sk20, 。..,sk2560
sk1= sk11, sk21, 。..,sk2561
我們以列表 (sk~0~, sk~1~) 表示用來簽名的 密鑰。接下來為了生成公鑰,我們將隨機的位字符串通過 H(。) 進行哈希運算,得到公鑰如下表:
pk0= H(sk10), H(sk20), 。..,H(sk2560)
pk1= H(sk11), H(sk21), 。..,H(sk2561)
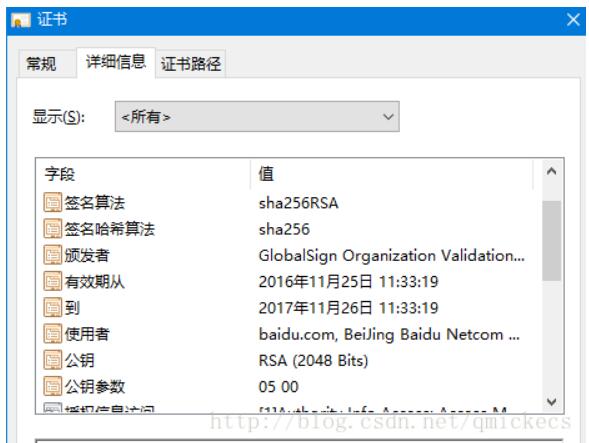
現(xiàn)在我們可以將公鑰 (pk~0~,pk~1~) 公布給所有人知道。比如說,我們可以把公鑰發(fā)給朋友,嵌入證書中,或是發(fā)布在 Keybase 上。
接著我們使用密鑰對 256 位消息 M 進行簽名。首先我們得將消息 M 重現(xiàn)為獨立的 256 位元(Bit,又稱“比特”):
M1, M2, 。.., M256 ∈ {0, 1}
簽名算法的其余部分非常簡單。我們從消息 M 的第 1 位至第 256 位,逐一相應(yīng)在密鑰列表中的其中一個密鑰上取出字符串。而所選密鑰取決于我們要簽名的消息每一位(bit)的值。
具體一點地說,對于 i = [1,256],如果第 i 位的消息位元 Mi = 0,我們會從 sk0 表中選擇第 i 個字符 (ski0) ,作為我們簽名的一部分;如果第 i 位的消息位元 Mi = 1,我們則從 sk1 表進行前述過程(即,如果我們要對消息 M 中的第 3 位進行簽名,而該位值為 0,則使用 sk0 中的第三位,sk03,作為我們簽名的一部分)。對每個消息位元完成此操作后,我們將選中的字符串連接,得到簽名。
過程如圖示說明,因為部分過程化簡,密鑰和消息長度只有 8 個 bit(位元)。要注意的是,每個色塊代表的都是不同的隨機 256 位字符串。
當(dāng)某個用戶(已經(jīng)知道公鑰 (pk0, pk1))收到消息 M 和簽名,她能夠輕易地驗證這個簽名。我們以 si 表示簽名中第 i 個組成部分,用戶能夠檢查相應(yīng)的消息 Mi 并計算哈希值 H(si) 。如果 Mi = 0 ,則哈希值必須匹配公鑰 pk0 中的元素;如果 Mi = 1 ,則哈希值必須匹配公鑰 pk1 中的元素。
如果簽名中的每個元素經(jīng)過哈希運算后,都能找到對應(yīng)的正確部分的公鑰,我們就會說這個簽名是有效的。以下是驗證過程圖示,簽名中至少有一個簽名元素:
如果你開始覺得 Lamport 的計劃有些瘋狂,你既是對的,也是錯的。
首先探討下這個數(shù)字簽名方法的弊端。我們會發(fā)現(xiàn), Lamport 方法的簽名和密鑰實在太大了,大約有數(shù)千 bits。而且更要命的是,這個方法存在嚴重的安全局限:每個密鑰只能被用來簽名一個消息,所以 Lamport 方法作為“一次性簽名” 在這里被拿來舉例。
這種安全局限為什么存在呢?回想一下, Lamport 簽名表明了在各個消息位元上可能的兩個密鑰之一。假如只需要簽署一條信息,這個簽名方法完全沒問題。然而,如果我簽署了兩條在每一個對應(yīng)位置 i 的 bit 值都不同的消息,然后連同密鑰一起發(fā)送出去,這可能導(dǎo)致大問題!
假設(shè)攻擊者從不同的消息得到兩個有效的簽名,她便能夠發(fā)起 “混合搭配(mix and match)”攻擊,成功偽造簽署第三條我從未簽名過的信息。以下圖示說明這個攻擊過程:
這個問題的嚴重程度取決于你簽名的消息的相異程度,以及有多少消息被攻擊者給截獲了。但總的來說,這肯定不是件好事。
讓我們總結(jié)一下 Lamport 簽名方法;它很簡單、快速,但它在實際應(yīng)用上還有很多不足之處。或許我們可以做一點優(yōu)化?
從一次性簽名到多次簽名:基于默克爾樹 (Merkle’s tree) 的簽名
Lamport 簽名方法是個好的開端,但是無法用單一密鑰簽名多條信息,是它最大的弊端。Martin Hellman 的學(xué)生 Ralph Merkle 由此得到大量啟發(fā),他很快地想到了一個聰明的解決辦法。
雖然我們不打算在這里展開解釋默克爾方法的步驟,我們還是來試著理清 Ralph 的想法。
我們現(xiàn)在的目標(biāo)是用 Lamport 簽名方法簽署 N 條信息。最直觀的方法是,以最初的 Lamport 方法生成 N 個不同的密鑰對,然后將所有公鑰關(guān)聯(lián)起來,集合成一個超巨大的 mega-key。(mega-key是我現(xiàn)編的術(shù)語。)
如果簽名者繼續(xù)拿著這么一把密鑰集合,她就可以對 N 條不同消息進行簽名,嚴格上來講這也只是一把 Lamport 密鑰。看起來,這樣就解決了密鑰重用的問題。驗證者也有對應(yīng)的公鑰能夠驗證所有收到的消息。沒有任何的 Lamport 密鑰被使用兩次。
很明顯的,這種方法很糟糕,因為時間成本太高了。
具體地說,上述這種天真的方法中,為了達到要求的簽名次數(shù),簽名者必須分發(fā)比普通 Lamport 公鑰還要大數(shù)倍的公鑰(簽名者還要繼續(xù)拿著同樣巨大的私鑰)。人們很可能會對這種結(jié)果感到不滿,也會反思有沒有辦法避免這種負作用產(chǎn)生。接下來,讓我們進入 Merkle 方法。
Merkle 方法希望能找到一個能簽署多條不同消息的方法,同時避免公鑰的成本線性激增。Merkle 方法的實現(xiàn)如下:
1.首先,生成 N 個獨立的 Lamport 密鑰,我們以 (PK1, SK1), 。.., (PKN, SKN) 表示之。
2.接下來,將每一個公鑰分別放到 Merkle hash tree (見下圖),并計算根節(jié)點哈希值。這個根節(jié)點就會成為Merkle簽名方法中的 “主公鑰”。
3.簽名者報關(guān)全部的 Lamport 密鑰(公鑰和私鑰),用于簽名。
關(guān)于 Merkle tree 的更多描述請點擊這里。概略地說,Merkle 方法提供了一種能收集不同的值,并用一個 “根” 哈希(例子中使用的哈希函數(shù),長度為 256 bits)代表所收集的值的方法。給出這個根哈希,就能簡單“證明” 某個元素存在于這個給出的哈希樹。而且這個證明的大小和葉節(jié)點數(shù)量成對數(shù)關(guān)系。
-Merkle tree,來自維基百科的解釋。Lamport 公鑰被放進葉節(jié)點中,然后根節(jié)點成為主公鑰。-
要簽名的時候,簽名者從 Merkle tree 中直接選擇公鑰,并用對應(yīng)的 Lamport 密鑰簽名。接著她將得到的簽名結(jié)果連接 Lamport 公鑰并附上“Merkle 證明”。Merkle root 可以來佐證該默克爾樹中包含選中的公鑰(即整個方法使用的公鑰)。最后簽名者將整個集合當(dāng)作消息簽名發(fā)送出去。
(驗證者只要直接將這個“簽名”分別解壓為 Lamport 簽名、 Lamport 公鑰、 Merkle 證明,就能進行驗證。驗證者能夠依靠拿到的 Lamport 公鑰驗證 Lamport 簽名,并用 Merkle 證明這把公鑰的確存在于 Merkle tree 中。只要滿足這三個條件,驗證者就能確信簽名是有效的。)
這個方法的缺點是會將“簽名”大小增加兩倍以上。不過,現(xiàn)在 Merkle 方法主要的公鑰只是一串簡單的哈希值,使得這個方法比上面提到的原始 Lamport 方法更為簡潔。
最后還有個優(yōu)化部分,密碼學(xué)強度的偽隨機數(shù)發(fā)生器能夠輸出生成各式各樣的密鑰,同時“壓縮”密鑰數(shù)據(jù)本身。這使得原先龐大的位元(顯然是隨機的)能夠轉(zhuǎn)換為簡短的“種子(seed)”。
很贊啦!
讓簽名和密鑰更有效率一點
Merkle 方法使得一次性簽名轉(zhuǎn)變?yōu)?N 次性簽名。構(gòu)造這種方法仍然需要基于某些一次性簽名方法,比如 Lamport 方法;但不幸的是,Lamport 方法的(帶寬)成本仍相對高昂。
有兩種主要的方法可以降低這些成本。第一種也是 Merkle 提出的;為了更好的解釋許多強大的簽名方法,我們優(yōu)先說明這項技術(shù)。
回想一下 Lamport 方法,要對一條 256 位的消息進行簽名,我們需要一個包含 512 個獨立密鑰(和公鑰)位串的向量,簽名本身就是 256 個密鑰位串的集合。(這些數(shù)字會被需要簽名的消息位元激活,位元可以是 “0” 或 “1” ,因此需要從兩張不同的密鑰表中提取適合的密鑰元素。 )
這里引發(fā)了新的思考:如果我們不對所有的消息位元進行簽名,會怎么樣呢?
更詳細點說,在 Lamport 方法中,我們通過輸出密鑰位串對一條消息的每個位元進行簽名——無論它的值是什么。如果我們不要同時簽名一條消息中 0 和 1 的位元,而是只簽名 1 的位元,那又會如何呢?這么做能夠?qū)⒐€和私鑰的大小減半,因為我們可以完全丟掉整條 sk0 列。
現(xiàn)在我們只有單一列位串的密鑰 sk1,。..,sk256,對消息的每個位元 Mi = 1我們都會輸出一個字符串 ski;對于消息的每個位元 Mi = 0我們都會輸出。..。..無(因為許多消息都會包含很多的 0 位元,這么做能縮減簽名大小,這些 0 位元將不再帶來任何成本)。
這種方法的明顯缺陷是:它極度不安全,所以請不要這么做!
舉例來說,假設(shè)有個攻擊者觀察到一條已經(jīng)被簽名的消息,消息開頭是“1111.。.”。現(xiàn)在攻擊者想要在不破壞簽名的情況下,將消息編輯成“0000.。.”,只需要刪掉這條簽名中的幾個組成部分即可!簡言之,雖然要將 0 位元“翻轉(zhuǎn)” 成 1 位元很困難,但反之要將 1 換成 0 就非常簡單了。
現(xiàn)在有了個解決辦法,而且它非常巧妙。
讓我們接著瞧瞧。雖然無法避免攻擊者將消息中的 1 改成 0 ,但我們能發(fā)現(xiàn)這些改動。只要將一個簡單的“校驗和(checksum)”附加到消息上,然后將消息和校驗和一起簽名。對于簽名驗證者來說,她必須驗證整份簽名的兩個值,也需要確定收到的校驗和是正確的。
我們使用的校驗和非常小:它由簡單的二進制整數(shù)組成,表示原始消息中的所有 0 位元數(shù)。
如果攻擊者試圖修改消息內(nèi)容(或是校驗和),使得部分 1 位元變成 0 位元,并沒有手段可以阻止她。但是這種攻擊會增加消息中的 0 位元數(shù),這會使得校驗和無效,驗證者從而會拒絕這個簽名。
當(dāng)然,機智的攻擊者可能還會試圖混淆校驗和(校驗和也和消息一起被簽名),增加校驗和的整數(shù)值來匹配她篡改的位元數(shù)。然而最關(guān)鍵的是,因為校驗和是二進制整數(shù),如果要增加校驗和的值,攻擊者勢必得將一些 0 位元轉(zhuǎn)換成 1 位元。又因為校驗和也被簽過名,這種簽名方法從源頭阻止這種轉(zhuǎn)換(將 0 換成 1),因此攻擊者無法得逞。
(如果你繼續(xù)記錄下去,的確會增加被簽名的“消息”的大小。在我們的例子中,一條 256 位的消息的校驗和,需要額外的 8 位元及增加相應(yīng)的簽名成本。不過,如果這條消息包含許多 0 位元,這么做對于縮減簽名大小仍然非常有效。)
 電子發(fā)燒友App
電子發(fā)燒友App










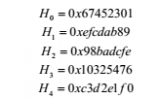











評論