對數放大器的原理和分類
對數放大器的原理和分類
對數放大器原理
針對上述的三種對數放大器,我們分別來講述其實現信號對數變換的原理。
基本對數放大器
基本對數放大器在IC設計中使用了跨導線性電路,因此也稱做跨導線性(Translinear)對數放大器。跨導線性電路是電流模電路的主要組成部分,是許多線性和非線性模擬集成電路的理論基礎。跨導線性的概念在1975年由Barrie Gillbert創立,跨導線性對數放大器就是基于雙極性(BJT)三極管的對數特性。如圖1
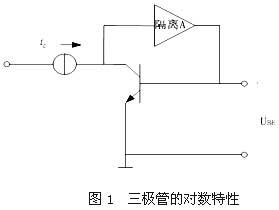
若將ic視為激勵信號電流,UBE看作響應信號電壓,將輸入偏流為零的隔離放大器接在集電極C與基極B之間以隔離iB的影響。
可以看出,理想BJT的UBE與其ic是理想的對數關系。等式中,Is是BJT的飽和電流,它與溫度密切相關。此外熱電壓UT也依賴于溫度。在集成的跨導線性對數放大器中這種受溫度影響的缺點已被一個具有同樣溫度變化特性的三極管修正,而且可以確保對數斜率的穩定性。
UY叫做對數斜率,固定電流IZ叫做對數截距(有關對數放大器的一些名詞將在后面予以說明)。
基帶對數放大器與解調對數放大器
對于高頻應用,常常選擇基帶對數放大器或解調對數放大器。盡管這兩種放大器在細節上有些不同,但原理是相同的,它不是采用一個放大器的對數特性而是用多個相同的線性放大器級聯來分段線性逼近對數函數。如圖2所示,這里只是一個理想的通用模型,其核心為一個限幅放大器,每個放大單元的傳遞函數如圖3所示,對于N個級聯限幅放大器構成的對數放大器, EK為限幅放大器的飽和電壓,A為放大倍,當輸入信號電壓小于臨界值EK/AN-1時,限幅放大器的每一級都不會飽和,因此,小于EK/AN-1的輸入信號可以得到充分的放大,此時輸出信號幅度是輸入信號幅度的AN-1倍。當輸入電壓大于EK/AN-1小于EK時,由于各級限幅的原因,輸入信號越大,飽和的級數越多。當輸入大于EK時,輸出則為NAEK。輸入信號幅度在EK/AN-1和EK之間的信號,其總的輸出電壓與輸入電壓的幅度可用下式表示:
VIN= EK/AN-M ,VOUT=,其中M為飽和的級數(M≤N)
實際的電路結構是:對于小信號采用增益為A的放大器,而大信號則采用單位增益放大器,稱之為A/1放大器,如圖4所示,限幅增益放大器和單位增益緩沖器并聯,輸出送加法器。解調對數放大器與基帶對數放大器雖然都采用上述的級聯限幅放大器,解調對數放大器不是將輸出直接累加,而是先檢波然后輸出累加,用級聯限幅放大器構成的對數放大器有兩種輸出:對數輸出和限幅輸出。許多應用中限幅輸出并不需要,但有些應用中,兩種輸出都是必須的。解調對數放大器的對數輸出一般包括幅度信息,而相位和頻率信息則被丟失。如果采用半波檢波器和延時補償,相位和頻率信息也可被保留。
對數放大器的分類
在許多文獻中,對數放大器的分類也是相當混亂的,根據實現對數函數依據的不同,有的將其分為二極管、三極管對數放大器和級聯對數放大器,有的將其分為真對數放大器和似對數放大器等等。但幾十年來,隨著半導體理論、工藝和模擬集成電路的發展,許多對數放大器實現的方法已經被淘汰,其分類方法也未盡科學。目前根據市場上現有的對數放大器結構和應用領域的不同,可將對數放大器分為三類:基本對數放大器、基帶對數放大器和解調對數放大器。
基本對數放大器也稱跨導線性(Translinear)對數放大器,它基于雙極性三極管(BJT)的對數特性來實現信號的對數變換。這類對數放大器可以響應緩慢變化的輸入信號,其特點是具有優良的直流精度和非常寬的動態范圍(高達180dB),缺點是交流特性差。
基帶對數放大器也稱視頻對數放大器(雖然很少用于視頻顯示相關的應用),它克服了基本對數放大器的缺點,能夠響應快速變化的輸入。其原理是采用了一種 “逐級壓縮”的技術,交流特性好,但動態范圍較小。
解調對數放大器也稱逐級檢波對數放大器,它具有分段線性近似性質,形成對數級聯后,可以得到很好的對數傳遞函數,在整個動態范圍內對數精度高,同基帶對數放大器相似,也采用多個級聯線性放大器,動態范圍大。
非常好我支持^.^
(10) 90.9%
不好我反對
(1) 9.1%
相關閱讀:
- [電子說] 經典電路分析:六倍程的電流對數放大器 2023-10-18
- [電子說] 對數放大器和定向耦合器可實現駐波比檢測 2023-06-10
- [電子說] 對數放大器芯片MS2351產品簡述 2023-03-24
- [電子說] 對數放大器芯片信號探測器芯片MS2351參數特性介紹 2023-03-30
- [電子說] 對數放大器和定向耦合器可實現駐波比檢測 2023-03-08
- [模擬技術] 集成直流對數放大器 2023-03-08
- [模擬技術] 射頻放大器的類型及其區別_射頻放大器穩定條件 2023-02-21
- [模擬技術] 對數放大器對不同信號類型的響應及均方根直流轉換器的使用 2023-02-02
( 發表人:admin )
