高精度溫度測量為工業自動化應用提供基本數據,以確保產品質量和安全。有許多類型的溫度傳感器可供選擇,每種傳感器都有其優點和缺點。本應用筆記重點介紹電阻溫度檢測器(RTD),并闡述了優化測量精度的設計要點。
電阻溫度檢測器
RTD包含一個元件,其電阻隨溫度變化。大多數元素是鉑、鎳或銅。鉑RTD提供最佳性能,因為鉑在大溫度范圍內具有最線性和可重復的溫度電阻關系。
通常,與熱電偶和熱敏電阻相比,RTD產生更穩定和可重復的輸出。因此,RTD可實現更高的測量精度。
高精度 RTD 測量設計選項
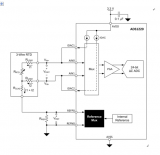
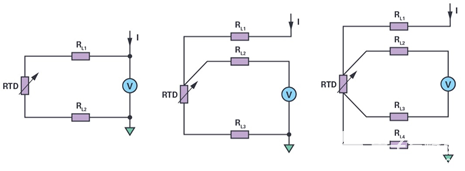
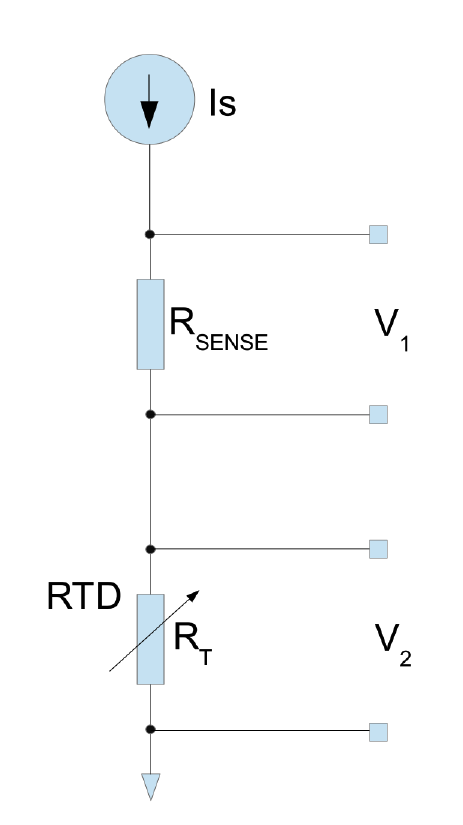
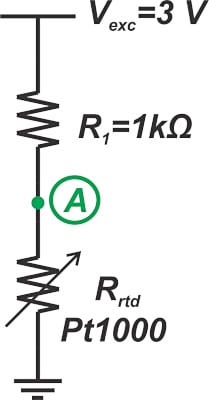
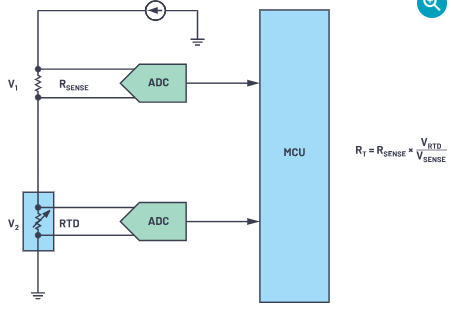
測量RTD的兩種最常見方法是恒流激勵(圖1)和恒壓激勵(圖2)。
目標是精確測量RTD電阻,并使用公式或查找表將其轉換為溫度。對于理想情況:
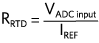
對于恒流勵磁,或
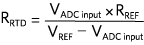
用于恒壓勵磁。
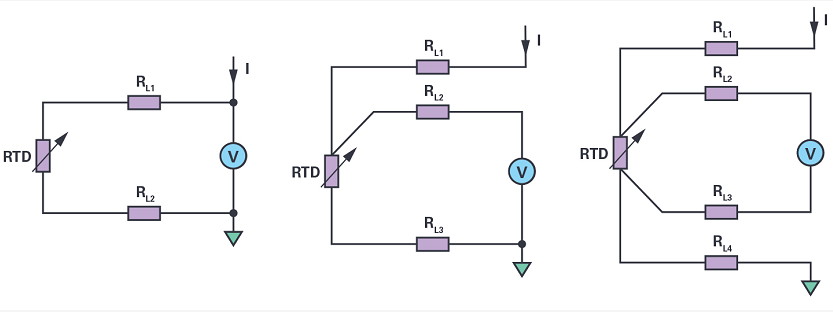
然而,在實踐中,RTD的引線具有電阻。長引線極大地影響了測量精度。因此,圖1和圖2所示電路測得的實際電阻為:
RTD + (2 × RWIRE),
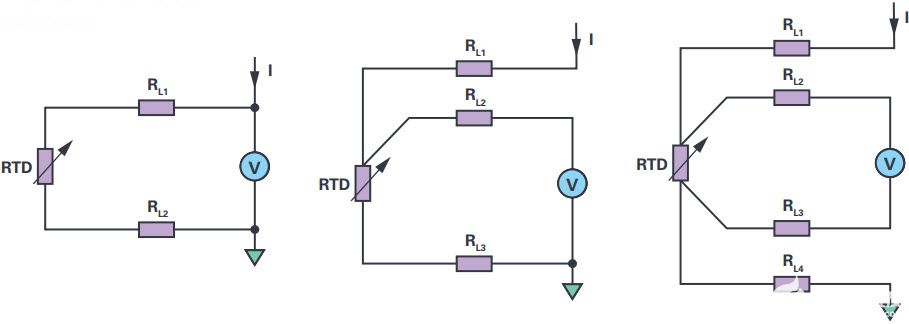
其中 R線是引線的電阻,假設兩根導線具有相同的電阻。雖然理論上可以接受,但相同的 R線意味著兩根電線的長度完全相同,并且由完全相同的材料制成。在關鍵溫度檢測應用中無法保證這樣的假設。因此,RTD 具有 3 線和 4 線配置,有助于消除引線造成的測量誤差。
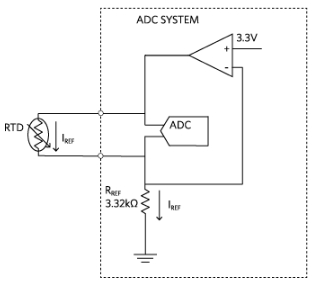
圖1.2線恒流勵磁配置。
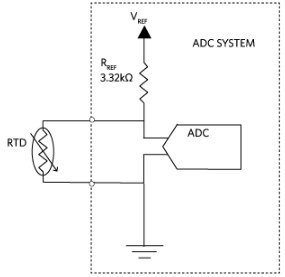
圖2.2線恒壓勵磁配置。
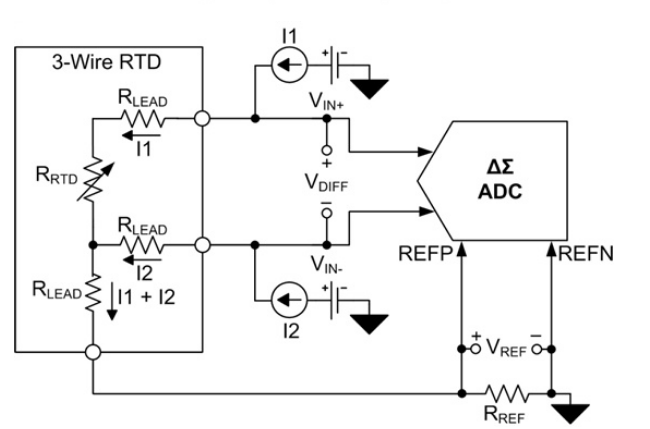
3線RTD配置
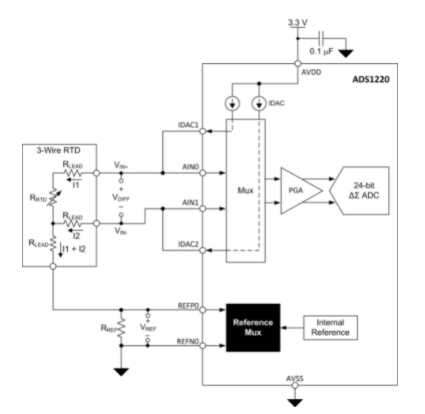
3線RTD的典型恒流和恒壓激勵電路分別如圖3和圖4所示。在這兩種情況下,ADC都對RTD + R的電阻進行采樣線3(其中 R線3是返回引線的電阻)。系統消除了 R線2,因為ADC輸入通常是高阻抗的,幾乎沒有電流流過R線2. 因此,ADC僅測量RTD和R兩端的電壓線3. R線3 導致測量誤差。然而,與2線配置相比,引線貢獻的誤差減少了約50%。
進一步提高測量精度的一種方法是在電路中添加一個模擬開關。然后,ADC測量電壓(VX) 在激勵信號的輸出端,并得到 R 的值線1. 通過假設 R線1 與 R 大致相同線3、R線3可以減去。參考圖3,在電流激勵配置中,R線1 電阻等于:
?

?
這種提高測量精度的方法確實需要額外的硬件,并增加了軟件的復雜性。

圖3.3線恒流勵磁配置。
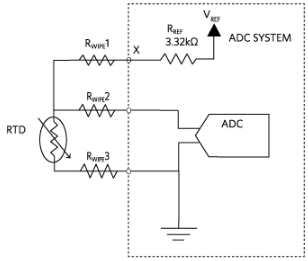
圖4.3線恒壓勵磁配置。
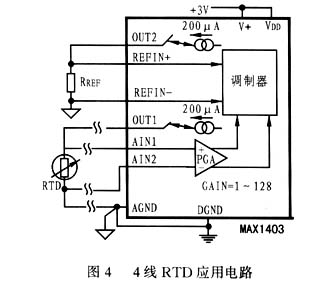
4線RTD配置
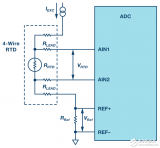
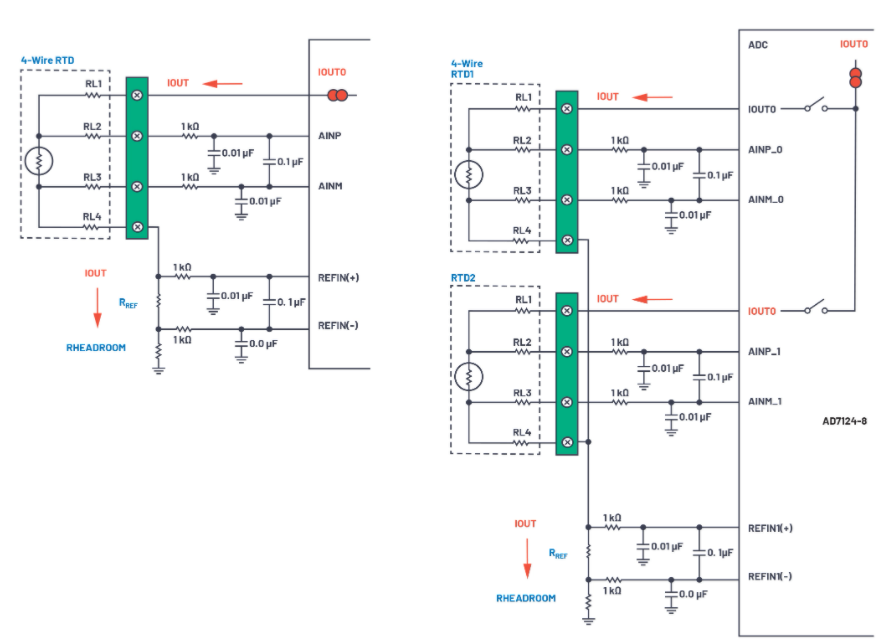
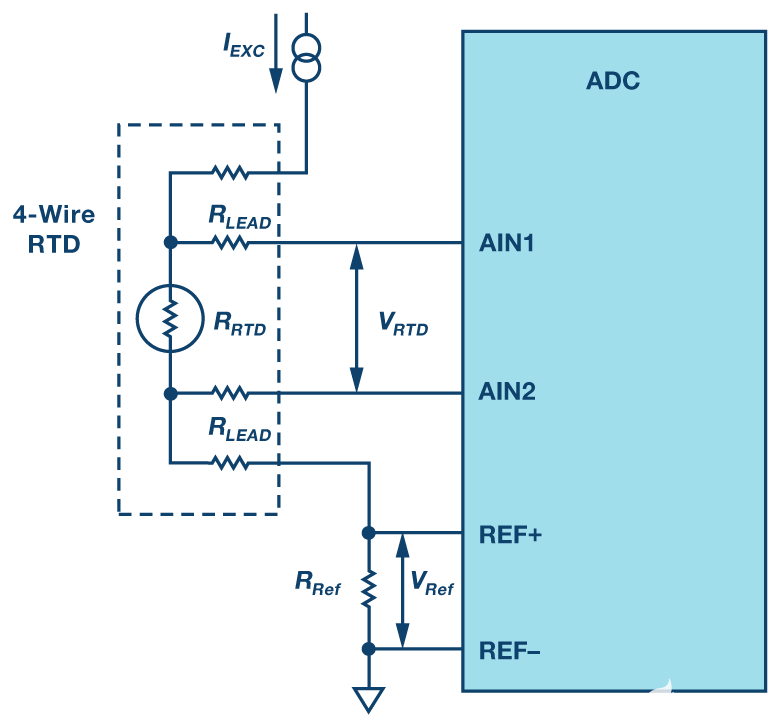
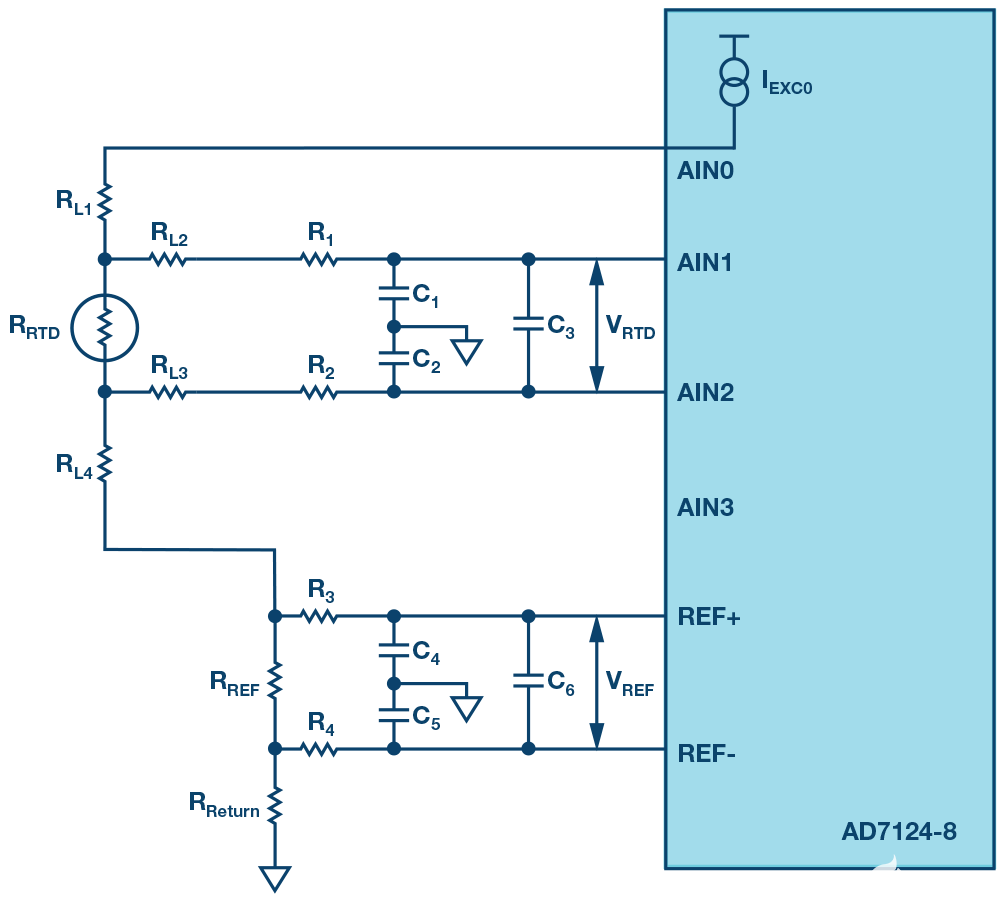
4線RTD配置提供最高的測量精度。圖5和圖6分別顯示了4線RTD的恒流激勵和恒壓激勵電路。對于電流激勵配置,
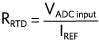
因為沒有電流通過R線2 或 R線3.因此,電壓過R端線2 + RTD + R線3與RTD兩端的電壓相同。不幸的是,當使用恒壓勵磁配置時,由于分壓器效應,R線1 和 R線4仍然會在RTD測量中產生誤差,除非ADC系統能夠測量激勵電壓輸出端的電壓(VX).如果電壓在 VX已知,則參考電流可以通過下式計算
信號鏈中的許多其他因素都會影響測量精度。這些因素包括ADC系統的輸入阻抗、ADC的分辨率、通過RTD的電流量、基準電壓源的穩定性以及激勵信號的穩定性。
ADC系統的輸入端必須具有高阻抗,以避免引線兩端的壓降(R線2 和 R線例如 3 線配置)。如果ADC沒有高阻抗輸入,則應在ADC輸入前添加緩沖器。

圖5.4線恒流勵磁配置。
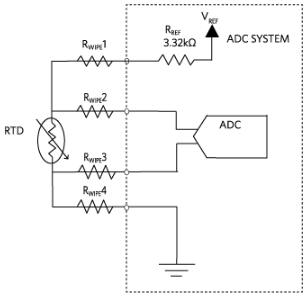
圖6.4線恒壓勵磁配置。
加熱誤差
雖然RTD是一個傳感器,但它也是一個電阻器。當電流通過電阻時,會出現功耗。耗散的功率使電阻升溫。這種自熱效應會在測量中產生誤差。必須仔細選擇激勵電流,以確保產生的誤差在誤差預算范圍內。計算自熱誤差的關鍵公式為
ΔT = (I2REF ×RRTD) × F
其中F是RTD的自熱系數,以mW/°C表示。 例如,浸沒在冰水中的PT-100鉑RTD,自熱系數為0.05°C/mW。當測量溫度為0°C時,R即熱處理等于100Ω。如果 I裁判設置為10mA,自發熱誤差變為
((0.01A)2× 100Ω) × 50°C/W = 0.5°C。
根據應用程序的不同,此錯誤可能是可接受的,也可能是不可接受的。對于高精度測量,較低的激勵電流可降低自發熱誤差。例如,如果我裁判降至1mA,自熱誤差變為0.005°C。 這種程度的錯誤更容易容忍。雖然降低激勵電流可降低自發熱誤差,但也減小了RTD兩端的電壓信號范圍,因此需要放大RTD信號,以便ADC可以提取更多的離散信號電平。另一種方法是使用更高分辨率的ADC。
到目前為止,所有討論的公式都涉及 I裁判或 V裁判.但是,如果這些激勵信號不穩定怎么辦?不穩定可能是由短期或長期漂移引起的。顯然,如果激勵信號變得不準確,則上述所有計算都有誤差。因此,需要定期校準。當然,工程師可以使用具有超低溫度漂移和長期漂移的超穩定基準電壓源。但是,通常此類設備非常昂貴。或者,比例溫度測量方法消除了由不準確的激勵信號引起的誤差。
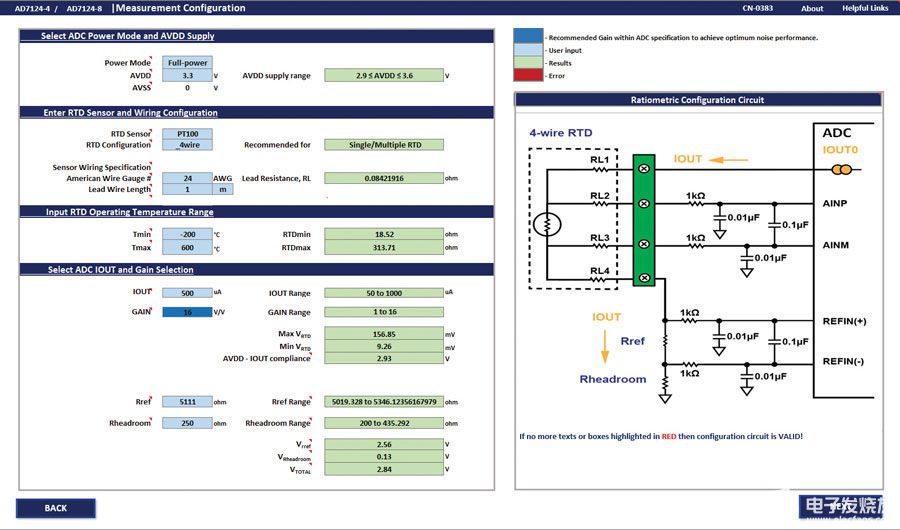
比例溫度測量
比率測量提供RTD電阻作為參考電阻之比的測量,而不是使用絕對電壓測量電阻。換句話說,R即熱處理將是 R 的函數裁判而不是 V裁判或我裁判.這使用相同的激勵信號來產生RTD兩端的電壓和ADC的基準電壓源。當激勵信號發生變化時,該變化會反映在RTD兩端的電壓和ADC的基準輸入上。圖7和圖8顯示了電流激勵和電壓激勵配置的比例測量電路。
一般ADC轉換公式為:
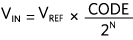
其中
VIN = ADC 輸入電壓
VREF = 參考電壓 (REFP - REFN)
CODE = ADC 代碼
N = ADC 的分辨率。
VIN等于RTD兩端的電壓。對于電流激勵模式
VIN = IREF × RRTD 和 VREF = IREF × RREF。
將VIN和VREF代入ADC轉換公式可得到,
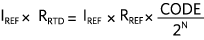
隨后,
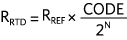
同樣,對于電壓激勵,
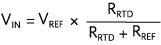
替換 V在進入ADC轉換公式產生,
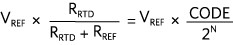
求解 R即熱處理給
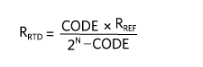
在這兩種情況下,簡化后,R即熱處理成為 R 的函數裁判和 ADC 代碼;因此,RTD測量的精度取決于R裁判.因此,在選擇基準電阻時,工程師必須選擇一個具有低溫和長期漂移的基準電阻。
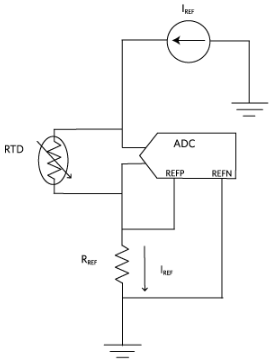
圖7.用于比率測量的電流激勵配置。
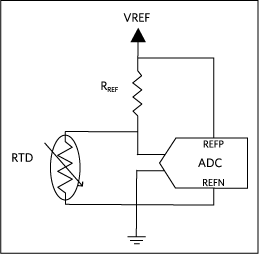
圖8.用于比率測量的電壓激勵配置。
RTD 至溫度轉換
無論電路對RTD電阻的測量效果如何,如果工程師沒有將RTD電阻精確轉換為溫度的好方法,那么所有的努力都將付諸東流。一種常見的方法是使用查找表。但是,如果分辨率要求高且測量溫度范圍較寬,則查找表將變得笨拙,并且該方法效果較差。另一種方法是計算溫度。
對于鉑RTD,Callendar-Van Dusen方程將電阻和溫度之間的關系描述為:
R(t) = R0 × (1 + A × t +B × t2+ (t - 100) × C × t3),
其中
R(t) = RTD 電阻
t = 溫度
R0 = RTD 在 0°C 時的電阻
A = 3.908 × 10-3
B = -5.775 × 10-7
C = -4.183 × 10-12 當 t < 0°C 時
t > 0°C 時 C = 0
?
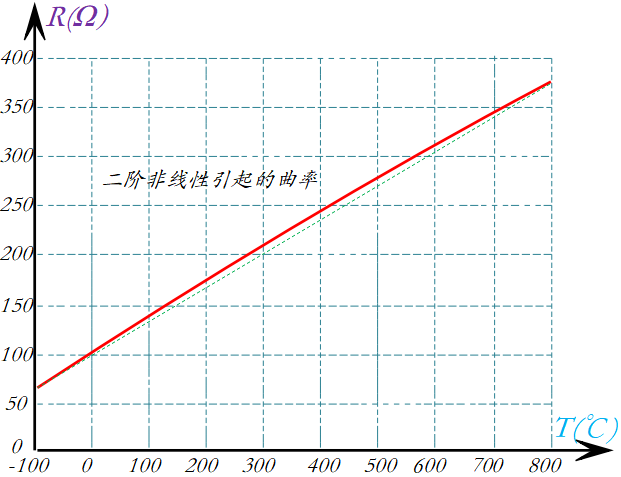
該公式提供了給定已知溫度的預期RTD電阻。如果感興趣的溫度范圍高于 0°C,則常數 C 變為 0,方程變為二次公式。求解二次方程很簡單。但是,如果溫度低于0°C并且C常數變為非零,則方程將變為困難的4階多項式。在這種情況下,多項式插值近似是一個非常有用的工具。這是一個微軟Excel解決方案:
在電子表格上,創建兩列數據。一列列出溫度。第二列列出了根據Callendar-Van Dusen方程計算得出的相應RTD電阻。
創建 X-Y 散點圖。
為繪圖添加多項式趨勢線。多項式的階數越高,給出的近似值越準確。
在“格式化趨勢線”菜單中選擇“在圖表上顯示方程式”。
得到的 PT100 在 t < 0°C 時的多項式方程為:
t = -1.6030e -13 × r6+ 2.0936e -10 × r5-3.6239e -8 × r4-4.2504e -6 × r3+ 2.5646e -3 × r2+ 2.2233 × r -2.4204e2
增加多項式系數的小數位可減少誤差。如上式所示,小數點后四位,溫度近似誤差小于0.005°C,大多數應用都可以容忍。
Maxim參考設計解決方案
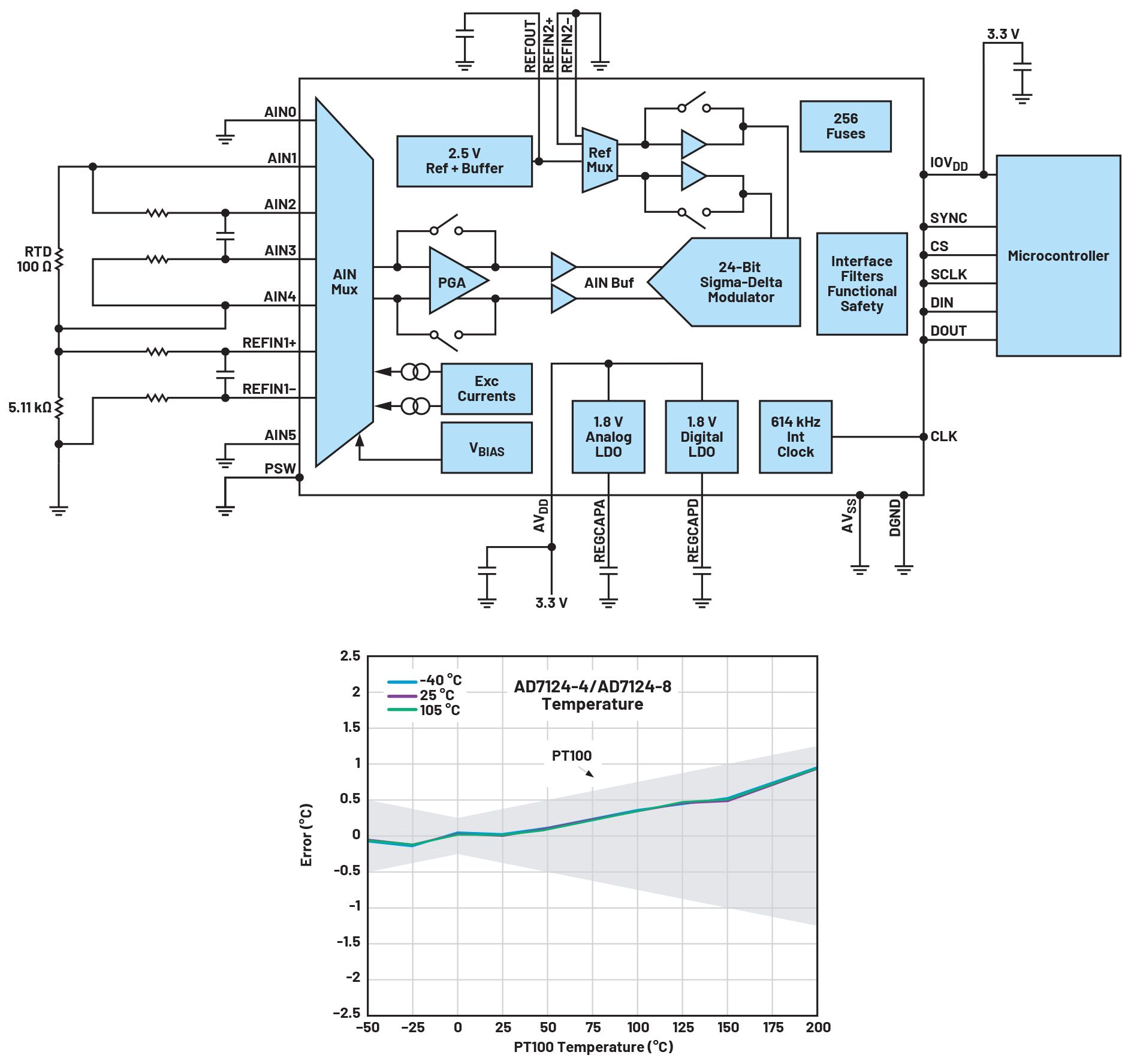
如上所述,MAXREFDES67# 參考設計實現了 4 線比率配置和多項式近似。此外,設計文件和固件可用于后續修改和實施。此外,該參考設計是適用于工業應用的完整通用模擬輸入。除了RTD測量外,這種獨特的24位前端還接受雙極性電壓和電流以及熱電偶(TC)輸入。MAXREFDES67#采用Maxim Integrated的超小型微型PLC外形,在-22°C至3°C范圍內具有高達0.1位的有效分辨率,溫度誤差低至±40.150%。 參考分別是 Omega HH41 溫度計、ETI 參考溫度計和福祿克 724 溫度校準器。將 MAXREFDES67# 連接的 RTD 探頭(Omega P-M-1/10-1/4-6-0-G-3)放置在福祿克 7341 校準槽中,并在 20°C 下進行校準。
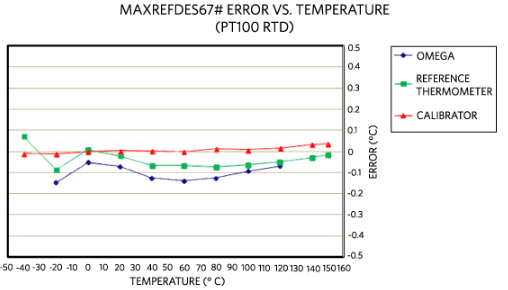
圖 12.MAXREFDES67# 誤差與溫度的關系,使用 Omega P-M-1/10-1/4-6-0-G-3,4 線 RTD,在 20°C 下校準。
結論
溫度是測量最多的工業參數。雖然使用比率法和多項式近似等技術的精密系統設計可以制造出非常精確的測量系統,但借助Maxim的參考設計系統,設計人員現在可以比以往更快地開發高精度RTD溫度測量或熱電偶測量系統。MAXREFDES67#允許修改和實現,是工業應用的完整通用模擬輸入。除RTD測量外,它還接受雙極性電壓、電流和熱電偶輸入,具有有效的分辨率和低測量誤差,使其比其他選項更有效。
審核編輯:郭婷
 電子發燒友App
電子發燒友App











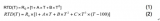

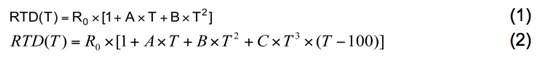
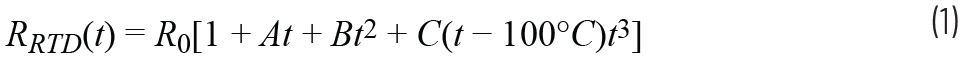

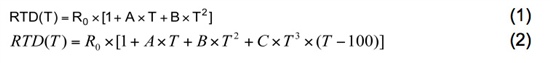
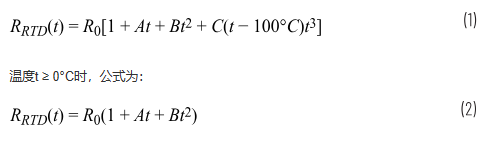











評論