本文介紹常見的電路——計數器,然后我們由計數器電路講解到分頻電路。
一、計數器
(1)計數器代碼
計數器,顧名思義就是在時鐘的節拍下進行計數,一個簡單的N位計數器的代碼如下所示,這個計數器從0計數到2^N - 1(共計數了2^N個數,也就是N位計數器):
1 module count#(parameter N=8)( 2 input clk, 3 input clear, 4 output[N-1:0] cnt_Q 5 ); 6 reg[N-1:0] cnt; 7 assign cnt_Q = cnt; 8 9 always@(posedge clk) 10 if(clear) 11 cnt <= 'h0; //同步清 0,高電平有效 12 else 13 cnt <= cnt+1'b1; //加法計數 14 15 endmodule
上述描述的計數器通過?clear?信號清除計數值,然后下一周期開始加?1?計數;當計數器計到能夠存儲的最大數值時, 例如本例為?8?個?1,即?8'hff?就會自動回到?0,然后開始下一輪計數。
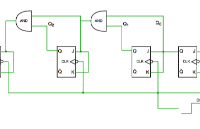
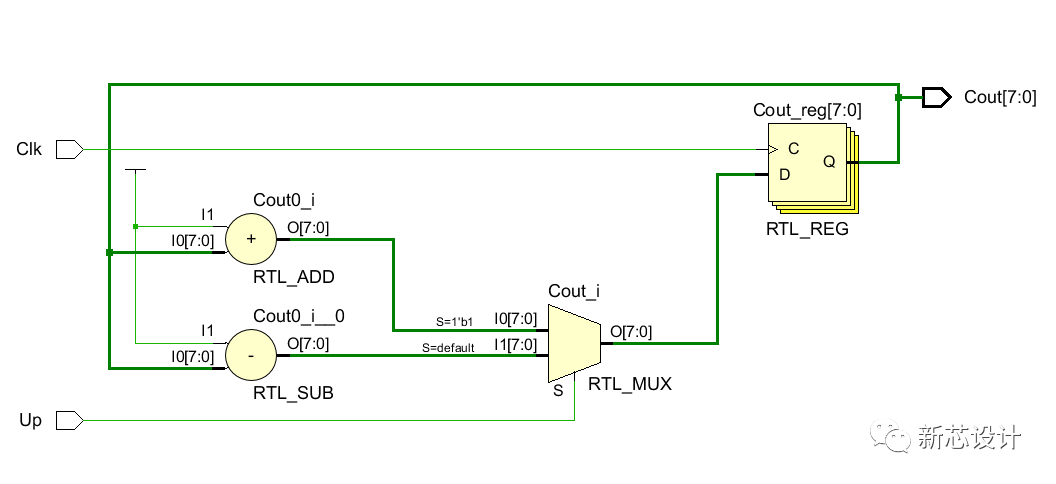
綜合得帶的電路如下所示:
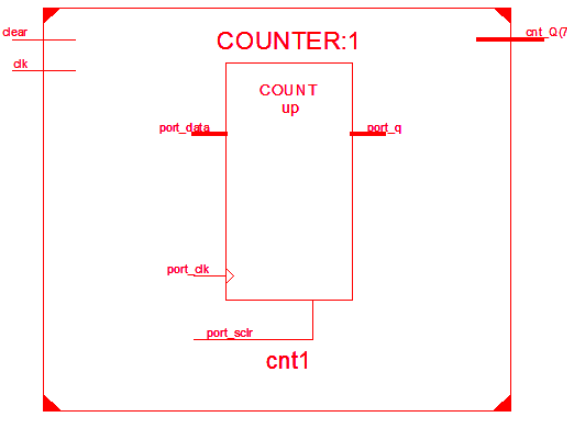
(2)計數器改進
如果想要實現?0~k?范圍內計數,其中k?≠?2^N?,可以將?always?語句修改為:
always@(posedge clk)
if(clear)
cnt <= 'h0; //同步清 0,高電平有效
else if(cnt==K)
cnt <= 'h0;
else
cnt <= cnt+1'b1; //減法計數
前面是累加計數,下面是一個既可以遞增也能遞減,且具備初始值裝載和復位的計數器,代碼如下所示:
1 module updown_count#(parameter N=8)( 2 input clk, 3 input clear, 4 input load, 5 input up_down, 6 input [N-1:0] preset_D, 7 output[N-1:0] cnt_Q 8 ); 9 reg[N-1:0] cnt; 10 assign cnt_Q = cnt; 11 12 always@(posedge clk) 13 if(clear) 14 cnt <= 'h0; //同步清 0,高電平有效 15 else if(load) 16 cnt <= preset_D; //同步預置 17 else if(up_down) 18 cnt <= cnt+1; //加法計數 19 else 20 cnt <= cnt-1; //減法計數 21 22 endmodule
二、計數器的用途
(1)基本的計數功能與分頻
計數器的基本功能顧名思義就是計數了,用來計數,產生某個信號等等。利用這個功能,可以實現信號的分頻,具體會在后面的分頻電路中進行描述。
(2)看門狗
計數器其實就可以設計成看門狗。在初始狀態時,看門狗電路首先裝載一個大數;當狀態機或者程序開始運行后,看門狗開始倒計數。如果狀態機或程序運行正常,每隔一段時間應發出指令或信號讓看門狗重新裝載一個大的初始值,并再次開始倒計數。如果看門狗減到 0?就認為程序或狀態機沒有正常工作,就需要強制整個系統復位。
上面的第二處改進的計數器電路描述就是一個看門狗電路,只要加上?cnt==0?作為看門復位狀態即可;而?load?信號則是狀態機或軟件給出的喂狗動作。
(3)特殊的有限狀態機
當狀態機要求沒有那么嚴格的時候,這個時候就可以用計數器的計數值當做狀態機的狀態,計數增加或者減少就是改變狀態。
三、分頻電路
(1)簡單的計數器
計數器實質是對輸入的驅動時鐘進行計數,所以計數器在某種意義上講,等同于對時鐘進行分頻。例如一個最大計數長度為N=2^n(從0計數到N-1)的計數器,也就是寄存器位數位n,那么寄存器最高位的輸出為N=2^n分頻,次高位為N/2分頻...例如下面的代碼:
1 module test#(parameter N=3)( 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 7 reg [N-1:0] div_reg ;//分頻計數器 8 always @(posedge clk or negedge rst_n) 9 if (rst_n == 1'b0 ) 10 div_reg <= 0 ; 11 else 12 div_reg <= div_reg + 1'b1 ; 13 14 assign clk_div = div_reg[N-1] ; 15 16 17 endmodule
該代碼描述的將一個3位的計數器最高位輸出,也就是計數長度為8(計數從0~7)波形如下所示:
可以看到最高位的輸出為輸入時鐘的8分頻。
當N不是2的整數次冪時,即N≠2^n時,從0計數到N-1,其最高位作為時鐘輸出(占空比不一定為 1:1)是輸入時鐘的1/N,也就是N分頻。我們來舉個例子,比如最大計數長度為5的計數器,即從0計數到4后又返回0,那么需要定義一個三位的寄存器。寄存器的計數過程為:
000-001-010-011-100-000-001-010-011-100-000-001-010-011-100-000-001-010-011-100······
我們取最高位,得到的信號變化就是:
0-0-0-0-1-0-0-0-0-0-1-0-0-0-0-1-0-0-0-0-1···
代碼如下所示:
1 module test#(parameter N=3)( 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 7 reg [N-1:0] div_reg ;//分頻計數器 8 always @(posedge clk or negedge rst_n) 9 if (rst_n == 1'b0 ) 10 div_reg <= 0 ; 11 else if(div_reg == 3'd4)//從0計數到4,然后返回到0,5分頻 12 div_reg <= 0; 13 else 14 div_reg <= div_reg + 1'b1 ; 15 16 assign clk_div = div_reg[N-1] ; 17 18 19 endmodule
仿真波形如下所示:
由此可以看到,每一個分頻后的時鐘周期=5倍原來的時鐘周期,因此是5分頻。
那么這個情況是不是也可以包含第一種情況呢?我們那設置為8分頻看看,即前面的3'd4改成3'd7,得到的仿真波形如下所示:
可以看到,計數器的最高位輸出也是輸入頻率的1/N。
因此我們得到結論:一個最大計數長度為N(從0計數到N-1)的計數器,其最高位的輸出,是輸入頻率的N分頻。
通常?ASIC?和?FPGA?中,時鐘都是全局信號,都需要通過?PLL?處理才能使用,但某些簡易場合,采用計數器輸出時鐘也是能夠使用的,只是需要注意時序約束。
(2)偶數倍分頻(占空比50%)
偶數分頻,也就是2分頻、4分頻、6分頻...這個還是比較簡單的,N(N當然是2的倍數)分頻,那么計數到N/2-1,然后時鐘翻轉:
例如N=6時,代碼如下所示:
1 module test#(parameter N=6)( 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 reg div_reg ; 7 reg [N-1:0] div_cnt ;//分頻計數器 8 always @(posedge clk or negedge rst_n) 9 if (rst_n == 1'b0 )begin 10 div_cnt <= 0 ; 11 div_reg <= 0 ; 12 end 13 else if(div_cnt == (N/2 - 1))begin 14 div_cnt <= 0; 15 div_reg <= ~div_reg ; 16 end 17 else 18 div_cnt <= div_cnt + 1'b1 ; 19 20 assign clk_div = div_reg ;
仿真波形如下所示:
當N=2的仿真波形如下所示:
(3)奇數倍分頻
①占空比接近50%
對于占空比不是50%的計數分頻,我們可以直接用上面的計數器方法,這里就不說了,我們介紹其他接近50%的占空比的方法,比如下面使用的狀態機分頻:
上圖的狀態機除了用一般的狀態機設計方式之外,我們也可以用簡單的計數器實現,這種方法如下所示:
假設時鐘分頻是N,則設置一個計數器,計數長度是N(即從0計數到N-1),然后在計數器為計數到(N-1)/2的時候,翻轉一下分頻時鐘信號;在計數器計數到為N-1的時候,再翻轉一下時鐘。
代碼如下所示:
1 module test#(parameter N=3)(//N分頻,這里是3分頻 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 7 reg [N-1:0] div_cnt ;//分頻計數器 8 reg div_reg ; 9 always @(posedge clk or negedge rst_n)begin 10 if (rst_n == 1'b0 )begin 11 div_cnt <= 0 ; 12 div_reg <= 1 ; 13 end else if (div_cnt == (N-1)/2)begin//計數到(N-1)/2,進行翻轉和繼續計數 14 div_reg <= ~div_reg; 15 div_cnt <= div_cnt + 1'b1 ; 16 end else if ( div_cnt == (N-1) )begin//計數到N-1,進行清零和翻轉 17 div_cnt <= 0 ; 18 div_reg <= ~div_reg; 19 end else 20 div_cnt <= div_cnt + 1'b1 ; 21 22 end 23 assign clk_div = (N == 1)?clk:div_reg ;//注意這里 24 25 26 endmodule
代碼中我們需要注意,在N= 1的情況,也就是不分頻的情況。仿真電路如下圖所示:
3分頻,N = 3:
5分頻,N= 5 :
不分頻,即N=1的仿真如下所示:
②占空比50%
產生具有50%占空比的奇數分頻時鐘的算法如下所示,假設N分頻(N是計數):
設置一個計數長度為N的上升沿計數器,和一個信號寄存器;信號寄存器在上升沿計數器為(N-1)/2的時候進行翻轉,然后再在計數到N-1的時候進行翻轉(這里相當于得到一個N分頻信號A)。
再設置一個計數長度為N的下降沿計數器,和另一個信號寄存器;信號寄存器在下降沿計數器為(N-1)/2的時候進行翻轉,然后再在計數到N-1的時候進行翻轉(這里相當于得到一個N分頻信號B)。
將A和B相或就可以得到占空比50%的奇數分頻信號;代碼實現如下:
1 module test#(parameter N=5)(//N分頻 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 7 reg sig_r ;//定義一個上升沿翻轉的信號 8 reg sig_f ;//定義一個下降沿翻轉的信號 9 reg [N-1:0] cnt_r;//上升沿計數器 10 reg [N-1:0] cnt_f;//下降沿計數器 11 12 wire clk_f ; 13 assign clk_f = ~clk ;//用來觸發下降沿計數器的時鐘 14 //由于同時使用上升沿和下降沿觸發器不好,因此我們為同一邊沿,都使用上升沿觸發 15 //只不過是將時鐘進行反向 16 17 always @(posedge clk or negedge rst_n)begin//上升沿計數 18 if(rst_n == 1'b0)begin 19 sig_r <= 0 ; 20 cnt_r <= 0 ; 21 end else if( cnt_r == (N-1)/2 )begin 22 sig_r <= ~sig_r ; 23 cnt_r <= cnt_r + 1 ; 24 end else if ( cnt_r == (N-1) )begin 25 sig_r <= ~sig_r ; 26 cnt_r <= 0 ; 27 end else 28 cnt_r <= cnt_r + 1 ; 29 end 30 31 always @(posedge clk_f or negedge rst_n)begin//下降沿計數 32 if(rst_n == 1'b0)begin 33 sig_f <= 0 ; 34 cnt_f <= 0 ; 35 end else if( cnt_f == (N-1)/2 )begin 36 sig_f <= ~sig_f ; 37 cnt_f <= cnt_f + 1 ; 38 end else if ( cnt_f == (N-1) )begin 39 sig_f <= ~sig_f ; 40 cnt_f <= 0 ; 41 end else 42 cnt_f <= cnt_f + 1 ; 43 end 44 45 assign clk_div = sig_f || sig_r ; 46 47 endmodule
仿真波形如下所示:
3分頻:
5分頻:
(4)任意整數倍分頻(接近50%)
在前面中,我們知道了一個最大計數長度為N(從0計數到N-1)的計數器,其最高位的輸出,是輸入頻率的N分頻,因此最簡單的任意分頻電路就是設計一個計數器,然后最高位輸出就是分頻的頻率了。雖然這這種方法很簡單,但是很顯然,這種方法的占空比是很糟糕的。因此我們要用其他的方法,也就是用其他的組合方式。
①占空比接近50%任意整數分頻
這種方法是取自偶數分頻和奇數分頻里面的接近50%占空比,實現的代碼如下所示:
1 module test #( parameter cfactor= 5)( 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 reg clk_loc; 7 //reg [15:0] cnt;//allowed maximum clock division factor is 65536 8 reg [7:0] cnt;//allowed maximum clock division factor is 256 9 10 assign clk_div = (cfactor==1)? clk : clk_loc; 11 //assign clk_div = ((rst==1) || (cfactor==1))? clk : clk_loc; 12 13 always@(posedge clk or negedge rst_n) 14 if(!rst_n)begin 15 cnt <= 'd0; 16 clk_loc = 1; 17 end 18 else begin 19 cnt <= cnt + 1'b1; 20 if(cnt==cfactor/2-1) 21 clk_loc = 0; 22 else if(cnt==cfactor-1) begin 23 cnt <= 'd0; 24 clk_loc = 1; 25 end 26 end 27 28 endmodule
2分頻的仿真圖,如下所示:
5分頻的仿真波形如下所示:
②占空比50%的任意整數分頻(重點)
這種方法是取自偶數分頻和奇數分頻都是50%占空比的組合,代碼如下所示:
1 module test#(parameter N=1)(//N分頻 2 input clk, 3 input rst_n, 4 output clk_div 5 ); 6 7 //奇數分頻 8 reg sig_r ;//定義一個上升沿翻轉的信號 9 reg sig_f ;//定義一個下降沿翻轉的信號 10 reg [N-1:0] cnt_r;//上升沿計數器 11 reg [N-1:0] cnt_f;//下降沿計數器 12 13 wire clk_f ; 14 assign clk_f = ~clk ;//用來觸發下降沿計數器的時鐘 15 //由于同時使用上升沿和下降沿觸發器不好,因此我們為同一邊沿,都使用上升沿觸發 16 //只不過是將時鐘進行反向 17 18 always @(posedge clk or negedge rst_n)begin//上升沿計數 19 if(rst_n == 1'b0)begin 20 sig_r <= 0 ; 21 cnt_r <= 0 ; 22 end 23 else begin 24 cnt_r <= cnt_r + 1 ; 25 if( cnt_r == (N-1)/2 )begin 26 sig_r <= ~sig_r ; 27 end else if ( cnt_r == (N-1) )begin 28 sig_r <= ~sig_r ; 29 cnt_r <= 0 ; 30 end 31 end 32 end 33 34 always @(posedge clk_f or negedge rst_n)begin//下降沿計數 35 if(rst_n == 1'b0)begin 36 sig_f <= 0 ; 37 cnt_f <= 0 ; 38 end 39 else begin 40 cnt_f <= cnt_f + 1 ; 41 if( cnt_f == (N-1)/2 )begin 42 sig_f <= ~sig_f ; 43 end else if ( cnt_f == (N-1) )begin 44 sig_f <= ~sig_f ; 45 cnt_f <= 0 ; 46 end 47 end 48 end 49 50 //偶數分頻 51 reg div_reg ; 52 reg [N-1:0] div_cnt ;//分頻計數器 53 always @(posedge clk or negedge rst_n)begin 54 if (rst_n == 1'b0 )begin 55 div_cnt <= 0 ; 56 div_reg <= 0 ; 57 end 58 else begin 59 div_cnt <= div_cnt + 1'b1 ; 60 if(div_cnt == (N/2 - 1))begin 61 div_cnt <= 0; 62 div_reg <= ~div_reg ; 63 end 64 end 65 end 66 assign clk_div = (N == 1)?clk: 67 ( N%2 == 1)?(sig_f || sig_r ): div_reg;//這里用來輸出分頻值。對2的取余操作是綜合的 68 69 endmodule
仿真波形如下所示:
5分頻:
6分頻:
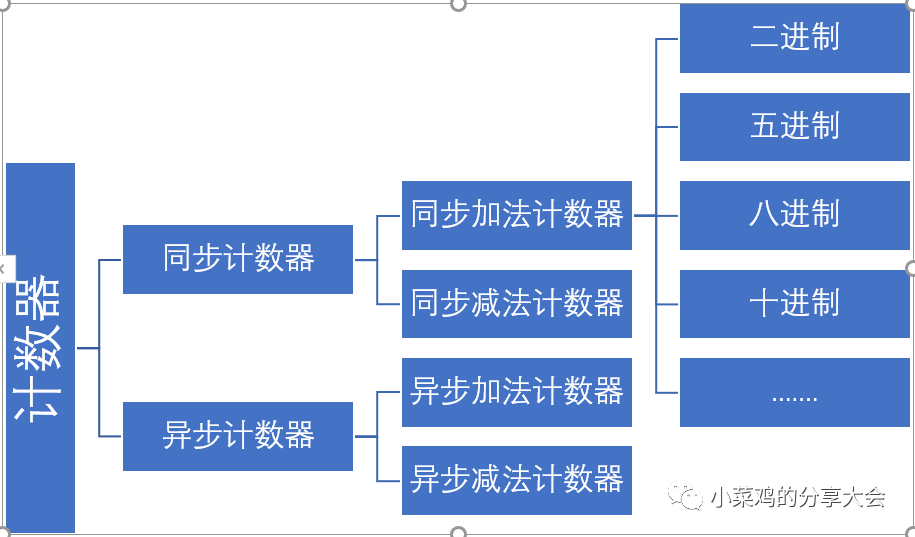
總結:本文介紹了計數器及其功能,主要是介紹了作為分頻器的功能。對于分頻器,如下所示:
編輯:hfy
 電子發燒友App
電子發燒友App

























評論