
?
式中a、b分別為橢球的半長軸、半短軸。
而圖3中的f1,f2分別表示橢球頂點到2個焦點,F1和F2的距離,其表達式如下:
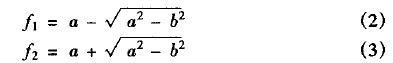
?
通過調整橢球的長短軸a和b的尺寸,可以改變橢球反射面的半焦距長度,從而可以改變出射光的角度,以確保出射光能照射在所需的照明區域內。
2.4 照度的計算方法
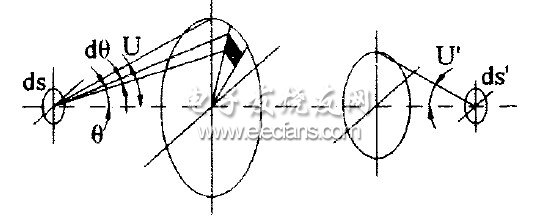
目前采用的照度計算公式通常都是基于如圖4的計算模型,其中,ds代表軸上點附近的物面上的微小面積ds',代表軸上點附近像面上的微小面積, U表示物方孔徑角、 U'表示像方孔徑角,而物面亮度為L像面亮度為L' ,物方ds在立體角U范圍內所發出的光通量Φ則可以表示為:
?
則從出瞳入射到像面微面積出ds'上的光通量φ' 為:
?
于是可得到像面的照度E' 為:
?
當物療空問和像方空間的介質一斂時,像面亮度L '等于物面亮度L與系統透射率τ0的乘積,即:
?
則(6)式就可以表示為:
?
?
圖4 照度計算模型示意圖
