晶振是晶體振蕩器的簡稱。晶體振蕩器是指從一塊石英晶體上按一定方位角切下薄片（簡稱為晶片），石英晶體諧振器，簡稱為石英晶體或晶體、晶振；而在封裝內部添加IC組成振蕩電路的晶體元件稱為晶體振蕩器。其產品一般用金屬外殼封裝，也有用玻璃殼、陶瓷或塑料封裝的。

　　晶振有著不同使用要求及特點，通分為以下幾類：普通晶振、溫補晶振、壓控晶振、溫控晶振等。在測試和使用時所供直流電源應沒有足以影響其準確度的紋波含量，交流電壓應無瞬變過程。測試儀器應有足夠的精度，連線合理布置，將測試及外圍電路對晶振指標的影響降至最低。

　　晶振的分類

　　根據晶振的功能和實現技術的不同，可以將晶振分為以下四類：

　　（1） 恒溫晶體振蕩器（以下簡稱OCXO）

　　這類型晶振對溫度穩定性的解決方案采用了恒溫槽技術，將晶體置于恒溫槽內，通過設置恒溫工作點，使槽體保持恒溫狀態，在一定范圍內不受外界溫度影響，達到穩定輸出頻率的效果。這類晶振主要用于各種類型的通信設備，包括交換機、SDH傳輸設備、移動通信直放機、GPS接收機、電臺、數字電視及軍工設備等領域。根據用戶需要，該類型晶振可以帶壓控引腳。OCXO的工作原理如下圖3所示：

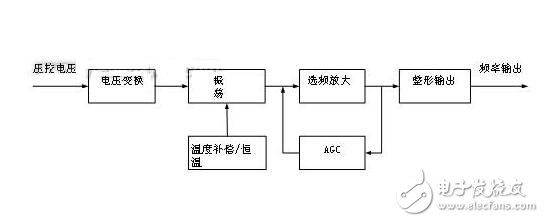
　　圖3恒溫晶體振蕩器原理框圖

　　OCXO的主要優點是，由于采用了恒溫槽技術，頻率溫度特性在所有類型晶振中是最好的，由于電路設計精密，其短穩和相位噪聲都較好。主要缺點是功耗大、體積大，需要5分鐘左右的加熱時間才能正常工作等。我公司生產的此類晶振的典型指標如下：

　　（2） 溫度補償晶體振蕩器（以下簡稱TCXO）。

　　其對溫度穩定性的解決方案采用了一些溫度補償手段，主要原理是通過感應環境溫度，將溫度信息做適當變換后控制晶振的輸出頻率，達到穩定輸出頻率的效果。傳統的TCXO是采用模擬器件進行補償，隨著補償技術的發展，很多數字化補償大TCXO開始出現，這種數字化補償的TCXO又叫DTCXO，用單片機進行補償時我們稱之為MCXO，由于采用了數字化技術，這一類型的晶振再溫度特性上達到了很高的精度，并且能夠適應更寬的工作溫度范圍，主要應用于軍工領域和使用環境惡劣的場合。在廣大研發人員的共同努力下，我公司自主開發出了高精度的MCXO，其設計原理和在世界范圍都是領先的，配以高度自動化的生產測試系統，其月產可以達到5000只，其設計原理如圖4。

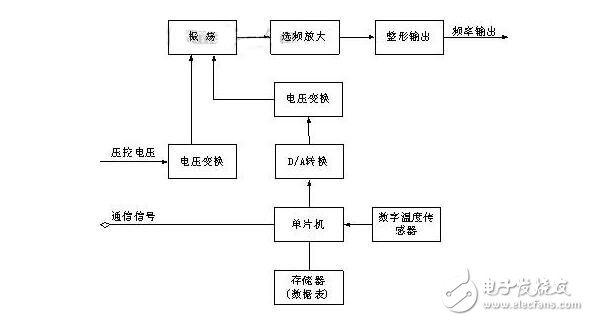
　　圖4 MCXO數字溫補晶振原理框圖

　　這類型晶振的典型的應用指標如下：

　　（3） 普通晶體振蕩器（SPXO）

　　這是一種簡單的晶體振蕩器，通常稱為鐘振，其工作原理為圖3中去除“壓控”、“溫度補償”和“AGC”部分，完全是由晶體的自由振蕩完成。這類晶振主要應用于穩定度要求不高的場合。

　　（4） 壓控晶體振蕩器（VCXO）

　　這是根據晶振是否帶壓控功能來分類，帶壓控輸入引腳的一類晶振叫VCXO，以上三種類型的晶振都可以帶壓控端口。

　　晶振的主要參數

　　1、頻率準確度：

　　在標稱電源電壓、標稱負載阻抗、基準溫度（25℃）以及其他條件保持不變，晶體振蕩器的頻率相對與其規定標稱值的最大允許偏差，即（fmax-fmin）/f0；

　　2、溫度穩定度：

　　其他條件保持不變，在規定溫度范圍內晶體振蕩器輸出頻率的最大變化量相對于溫度范圍內輸出頻率極值之和的允許頻偏值，即（fmax-fmin）/（fmax+fmin）；

　　3、頻率調節范圍：

　　通過調節晶振的某可變元件改變輸出頻率的范圍。

　　4、調頻（壓控）特性：

　　包括調頻頻偏、調頻靈敏度、調頻線性度。

　　①調頻頻偏：壓控晶體振蕩器控制電壓由標稱的最大值變化到最小值時輸出頻率差。

　　②調頻靈敏度：壓控晶體振蕩器變化單位外加控制電壓所引起的輸出頻率的變化量。

　　③調頻線性度：是一種與理想直線（最小二乘法）相比較的調制系統傳輸特性的量度。

　　5、負載特性：

　　其他條件保持不變，負載在規定變化范圍內晶體振蕩器輸出頻率相對于標稱負載下的輸出頻率的最大允許頻偏。

　　6、電壓特性：

　　其他條件保持不變，電源電壓在規定變化范圍內晶體振蕩器輸出頻率相對于標稱電源電壓下的輸出頻率的最大允許頻偏。

　　7、雜波：

　　輸出信號中與主頻無諧波（副諧波除外）關系的離散頻譜分量與主頻的功率比，用dBc表示。

　　8、諧波：

　　諧波分量功率Pi與載波功率P0之比，用dBc表示。

　　9、頻率老化：

　　在規定的環境條件下，由于元件（主要是石英諧振器）老化而引起的輸出頻率隨時間的系統漂移過程。通常用某一時間間隔內的頻差來量度。對于高穩定晶振，由于輸出頻率在較長的工作時間內呈近似線性的單方向漂移，往往用老化率（單位時間內的相對頻率變化）來量度。

　　10、日波動：

　　指振蕩器經過規定的預熱時間后，每隔一小時測量一次，連續測量24小時，將測試數據按S=（fmax-fmin）/f0式計算，得到日波動。

　　11、開機特性：

　　在規定的預熱時間內，振蕩器頻率值的最大變化，用V=（fmax-fmin）/f0表示。

　　12、相位噪聲：

　　短期穩定度的頻域量度。用單邊帶噪聲與載波噪聲之比￡（f）表示，￡；（f）與噪聲起伏的頻譜密度Sφ（f）和頻率起伏的頻譜密度Sy（f）直接相關，由下式表示：

　　f2S（f）=f02Sy（f）=2f2￡；（f）

　　f—傅立葉頻率或偏離載波頻率；f0—載波頻率。