對于電容退耦,很多資料中都有涉及,但是闡述的角度不同。有些是從局部電荷存儲(即儲能)的角度來說明,有些是從電源分配系統的阻抗的角度來說明,還有些資料的說明更為混亂,一會提儲能,一會提阻抗,因此很多人在看資料的時候感到有些迷惑。其實,這兩種提法,本質上是相同的,只不過看待問題的視角不同而已。為了讓大家有個清楚的認識,本文分別介紹一下這兩種解釋。
1、從儲能的角度來說明電容退耦原理。
在制作電路板時,通常會在負載芯片周圍放置很多電容,這些電容就起到電源退耦作用。
其原理可用圖 1 說明。
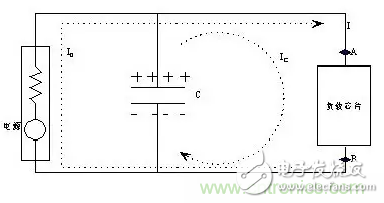
圖 1 去耦電路
當負載電流不變時,其電流由穩壓電源部分提供,即圖中的 I0,方向如圖所示。此時電容兩端電壓與負載兩端電壓一致,電流 Ic 為 0,電容兩端存儲相當數量的電荷,其電荷數量和電容量有關。當負載瞬態電流發生變化時,由于負載芯片內部晶體管電平轉換速度極快,必須在極短的時間內為負載芯片提供足夠的電流。但是穩壓電源無法很快響應負載電流的變化,因此,電流 I0 不會馬上滿足負載瞬態電流要求,因此負載芯片電壓會降低。但是由于電容電壓與負載電壓相同,因此電容兩端存在電壓變化。對于電容來說電壓變化必然產生電流,此時電容對負載放電,電流 Ic 不再為 0,為負載芯片提供電流。根據電容等式:
(公式 1)
只要電容量 C 足夠大,只需很小的電壓變化,電容就可以提供足夠大的電流,滿足負載瞬態電流的要求。這樣就保證了負載芯片電壓的變化在容許的范圍內。這里,相當于電容預先存儲了一部分電能,在負載需要的時候釋放出來,即電容是儲能元件。儲能電容的存在使負載消耗的能量得到快速補充,因此保證了負載兩端電壓不至于有太大變化,此時電容擔負的是局部電源的角色。
從儲能的角度來理解電源退耦,非常直觀易懂,但是對電路設計幫助不大。從阻抗的角度理解電容退耦,能讓我們設計電路時有章可循。實際上,在決定電源分配系統的去耦電容量的時候,用的就是阻抗的概念。
2、從阻抗的角度來理解退耦原理。
將圖 1 中的負載芯片拿掉,如圖 2 所示。從 AB 兩點向左看過去,穩壓電源以及電容退耦系統一起,可以看成一個復合的電源系統。這個電源系統的特點是:不論 AB 兩點間負載瞬態電流如何變化,都能保證 AB 兩點間的電壓保持穩定,即 AB 兩點間電壓變化很小。
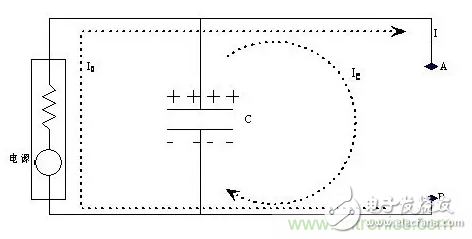
圖片 2 電源部分
我們可以用一個等效電源模型表示上面這個復合的電源系統,如圖 3
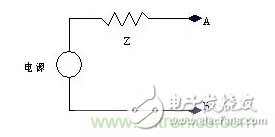
圖 3 等效電源
對于這個電路可寫出如下等式:
(公式 2)
我們的最終設計目標是,不論 AB 兩點間負載瞬態電流如何變化,都要保持 AB 兩點間電壓變化范圍很小,根據公式 2,這個要求等效于電源系統的阻抗 Z 要足夠低。在圖 2 中,我們是通過去耦電容來達到這一要求的,因此從等效的角度出發,可以說去耦電容降低了電源系統的阻抗。另一方面,從電路原理的角度來說,可得到同樣結論。電容對于交流信號呈現低阻抗特性,因此加入電容,實際上也確實降低了電源系統的交流阻抗。
從阻抗的角度理解電容退耦,可以給我們設計電源分配系統帶來極大的方便。實際上,電源分配系統設計的最根本的原則就是使阻抗最小。最有效的設計方法就是在這個原則指導下產生的。
正確使用電容進行電源退耦,必須了解實際電容的頻率特性。理想電容器在實際中是不存在的,這就是為什么經常聽到“電容不僅僅是電容”的原因。
實際的電容器總會存在一些寄生參數,這些寄生參數在低頻時表現不明顯,但是高頻情況下,其重要性可能會超過容值本身。圖 4 是實際電容器的 SPICE 模型,圖中,ESR 代表等效串聯電阻,ESL 代表等效串聯電感或寄生電感,C 為理想電容。
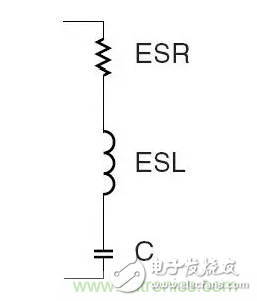
圖 4 電容模型
等效串聯電感(寄生電感)無法消除,只要存在引線,就會有寄生電感。這從磁場能量變化的角度可以很容易理解,電流發生變化時,磁場能量發生變化,但是不可能發生能量躍變,表現出電感特性。寄生電感會延緩電容電流的變化,電感越大,電容充放電阻抗就越大,反應時間就越長。等效串聯電阻也不可消除的,很簡單,因為制作電容的材料不是超導體。
討論實際電容特性之前,首先介紹諧振的概念。對于圖 4 的電容模型,其復阻抗為:
(公式 3)

時,此時容性阻抗矢量與感性阻抗之差為 0,電容的總阻抗最小,表現為純電阻特性。該頻率點就是電容的自諧振頻率。自諧振頻率點是區分電容是容性還是感性的分界點,高于諧振頻率時,“電容不再是電容”,因此退耦作用將下降。因此,實際電容器都有一定的工作頻率范圍,只有在其工作頻率范圍內,電容才具有很好的退耦作用,使用電容進行電源退耦時要特別關注這一點。寄生電感(等效串聯電感)是電容器在高于自諧振頻率點之后退耦功能被消弱的根本原因。圖 5 顯示了一個實際的 0805 封裝 0.1uF 陶瓷電容,其阻抗隨頻率變化的曲線。
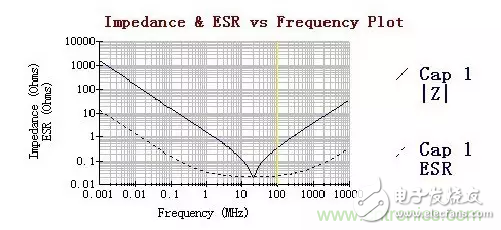
圖 5 電容阻抗特性
電容的自諧振頻率值和它的電容值及等效串聯電感值有關,使用時可查看器件手冊,了解該項參數,確定電容的有效頻率范圍。下面列出了 AVX 生產的陶瓷電容不同封裝的各項參數值。
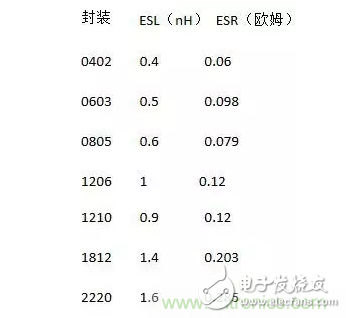
電容的等效串聯電感和生產工藝和封裝尺寸有關,同一個廠家的同種封裝尺寸的電容,其等效串聯電感基本相同。通常小封裝的電容等效串聯電感更低,寬體封裝的電容比窄體封裝的電容有更低的等效串聯電感。
既然電容可以看成 RLC 串聯電路,因此也會存在品質因數,即 Q 值,這也是在使用電容時的一個重要參數。
電路在諧振時容抗等于感抗,所以電容和電感上兩端的電壓有效值必然相等,電容上的電壓有效值 UC=I*1/ωC=U/ωCR=QU,品質因數 Q=1/ωCR,這里 I 是電路的總電流。電感上的電壓有效值 UL=ωLI=ωL*U/R=QU,品質因數Q=ωL/R。因為:UC=UL 所以 Q=1/ωCR=ωL/R。電容上的電壓與外加信號電壓 U 之比 UC/U=(I*1/ωC)/RI=1/ωCR=Q。電感上的電壓與外加信號電壓 U 之比 UL/U=ωLI/RI=ωL/R=Q。從上面分析可見,電路的品質因數越高,電感或電容上的電壓比外加電壓越高。
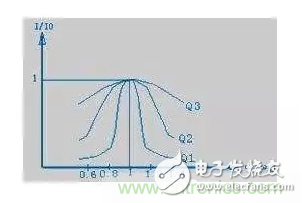
圖 6 Q 值的影響
Q 值影響電路的頻率選擇性。當電路處于諧振頻率時,有最大的電流,偏離諧振頻率時總電流減小。我們用 I/I0 表示通過電容的電流與諧振電流的比值,即相對變化率。表示頻率偏離諧振頻率程度。圖 6 顯示了 I/I0 與關系曲線。這里有三條曲線,對應三個不同的 Q 值,其中有 Q1》Q2》Q3。從圖中可看出當外加信號頻率 ω 偏離電路的諧振頻率 ω0時,I/I0 均小于 1。Q 值越高在一定的頻偏下電流下降得越快,其諧振曲線越尖銳。也就是說電路的選擇性是由電路的品質因素 Q 所決定的,Q 值越高選擇性越好。
在電路板上會放置一些大的電容,通常是坦電容或電解電容。這類電容有很低的 ESL,但是 ESR 很高,因此 Q 值很低,具有很寬的有效頻率范圍,非常適合板級電源濾波。
當電容安裝到電路板上后,還會引入額外的寄生參數,從而引起諧振頻率的偏移。充分理解電容的自諧振頻率和安裝諧振頻率非常重要,在計算系統參數時,實際使用的是安裝諧振頻率,而不是自諧振頻率,因為我們關注的是電容安裝到電路板上之后的表現。
電容在電路板上的安裝通常包括一小段從焊盤拉出的引出線,兩個或更多的過孔。我們知道,不論引線還是過孔都存在寄生電感。寄生電感是我們主要關注的重要參數,因為它對電容的特性影響最大。電容安裝后,可以對其周圍一小片區域有效去耦,這涉及到去耦半徑問題,本文后面還要詳細講述。現在我們考察這樣一種情況,電容要對距離它 2 厘米處的一點去耦,這時寄生電感包括哪幾部分。首先,電容自身存在寄生電感。從電容到達需要去耦區域的路徑上包括焊盤、一小段引出線、過孔、2 厘米長的電源及地平面,這幾個部分都存在寄生電感。相比較而言,過孔的寄生電感較大。可以用公式近似計算一個過孔的寄生電感有多大。 公式為
其中:L 是過孔的寄生電感,單位是 nH。h 為過孔的長度,和板厚有關,單位是英寸。d為過孔的直徑,單位是英寸。下面就計算一個常見的過孔的寄生電感,看看有多大,以便有一個感性認識。設過孔的長度為 63mil(對應電路板的厚度 1.6 毫米,這一厚度的電路板很常見),過孔直徑 8mil,根據上面公式得:
這一寄生電感比很多小封裝電容自身的寄生電感要大,必須考慮它的影響。過孔的直徑越大,寄生電感越小。過孔長度越長,電感越大。下面我們就以一個 0805 封裝 0.01uF 電容為例,計算安裝前后諧振頻率的變化。參數如下:容值:C=0.01uF。電容自身等效串聯電感:ESL=0.6 nH。安裝后增加的寄生電感:Lmount=1.5nH。
電容的自諧振頻率:
安裝后的總寄生電感:0.6+1.5=2.1nH。注意,實際上安裝一個電容至少要兩個過孔,寄生電感是串聯的,如果只用兩個過孔,則過孔引入的寄生電感就有 3nH。但是在電容的每一端都并聯幾個過孔,可以有效減小總的寄生電感量,這和安裝方法有關。
安裝后的諧振頻率為:
可見,安裝后電容的諧振頻率發生了很大的偏移,使得小電容的高頻去耦特性被消弱。在進行電路參數設計時,應以這個安裝后的諧振頻率計算,因為這才是電容在電路板上的實際表現。
安裝電感對電容的去耦特性產生很大影響,應盡量減小。實際上,如何最大程度的減小安裝后的寄生電感,是一個非常重要的問題。
從電源系統的角度進行去耦設計
先插一句題外話,很多人在看資料時會有這樣的困惑,有的資料上說要對每個電源引腳加去耦電容,而另一些資料并不是按照每個電源引腳都加去偶電容來設計的,只是說在芯片周圍放置多少電容,然后怎么放置,怎么打孔等等。那么到底哪種說法及做法正確呢?我在剛接觸電路設計的時候也有這樣的困惑。其實,兩種方法都是正確的,只不過處理問題的角度不同。看過本文后,你就徹底明白了。
上一節講了對引腳去耦的方法,這一節就來講講另一種方法,從電源系統的角度進行去耦設計。該方法本著這樣一個原則:在感興趣的頻率范圍內,使整個電源分配系統阻抗最低。其方法仍然是使用去耦電容。
電源去耦涉及到很多問題:總的電容量多大才能滿足要求?如何確定這個值?選擇那些電容值?放多少個電容?選什么材質的電容?電容如何安裝到電路板上?電容放置距離有什么要求?下面分別介紹。
著名的 Target Impedance(目標阻抗)
目標阻抗(Target Impedance)定義為:
(公式 4)

該定義可解釋為:能滿足負載最大瞬態電流供應,且電壓變化不超過最大容許波動范圍的情況下,電源系統自身阻抗的最大值。超過這一阻抗值,電源波動將超過容許范圍。如果你對阻抗和電壓波動的關系不清楚的話,請回顧“電容退耦的兩種解釋”一節。
對目標阻抗有兩點需要說明:
1、目標阻抗是電源系統的瞬態阻抗,是對快速變化的電流表現出來的一種阻抗特性。
2、目標阻抗和一定寬度的頻段有關。在感興趣的整個頻率范圍內,電源阻抗都不能超過這個值。阻抗是電阻、電感和電容共同作用的結果,因此必然與頻率有關。感興趣的整個頻率范圍有多大?這和負載對瞬態電流的要求有關。顧名思義,瞬態電流是指在極短時間內電源必須提供的電流。如果把這個電流看做信號的話,相當于一個階躍信號,具有很寬的頻譜,這一頻譜范圍就是我們感興趣的頻率范圍。
如果暫時不理解上述兩點,沒關系,繼續看完本文后面的部分,你就明白了。
需要多大的電容量
有兩種方法確定所需的電容量。第一種方法利用電源驅動的負載計算電容量。這種方法沒有考慮 ESL 及 ESR 的影響,因此很不精確,但是對理解電容量的選擇有好處。第二種方法就是利用目標阻抗(Target Impedance)來計算總電容量,這是業界通用的方法,得到了廣泛驗證。你可以先用這種方法來計算,然后做局部微調,能達到很好的效果,如何進行局部微調,是一個更高級的話題。下面分別介紹兩種方法。
方法一:利用電源驅動的負載計算電容量
設負載(容性)為 30pF,要在 2ns 內從 0V 驅動到 3.3V,瞬態電流為:
(公式 5)
如果共有 36 個這樣的負載需要驅動,則瞬態電流為:36*49.5mA=1.782A。假設容許電壓波動為:3.3*2.5%=82.5 mV,所需電容量為:
C=I*dt/dv=1.782A*2ns/0.0825V=43.2nF
說明:所加的電容實際上作為抑制電壓波紋的儲能元件,該電容必須在 2ns 內為負載提供1.782A 的電流,同時電壓下降不能超過 82.5 mV,因此電容值應根據 82.5 mV 來計算。記住:電容放電給負載提供電流,其本身電壓也會下降,但是電壓下降的量不能超過 82.5mV(容許的電壓波紋)。這種計算沒什么實際意義,之所以放在這里說一下,是為了讓大家對去耦原理認識更深。
方法二:利用目標阻抗計算電容量(設計思想很嚴謹,要吃透)
為了清楚的說明電容量的計算方法,我們用一個例子。要去耦的電源為 1.2V,容許電壓波動為 2.5%,最大瞬態電流 600mA,
第一步:計算目標阻抗
第二步:確定穩壓電源頻率響應范圍。
和具體使用的電源片子有關,通常在 DC 到幾百 kHz 之間。這里設為 DC 到 100kHz。在100kHz 以下時,電源芯片能很好的對瞬態電流做出反應,高于 100kHz 時,表現為很高的阻抗,如果沒有外加電容,電源波動將超過允許的 2.5%。為了在高于 100kHz 時仍滿足電壓波動小于 2.5%要求,應該加多大的電容?
第三步:計算 bulk 電容量
當頻率處于電容自諧振點以下時,電容的阻抗可近似表示為:頻率 f 越高,阻抗越小,頻率越低,阻抗越大。在感興趣的頻率范圍內,電容的最大阻抗不能超過目標阻抗,因此使用 100kHz 計算(電容起作用的頻率范圍的最低頻率,對應電容最高阻抗)。
第四步:計算 bulk 電容的最高有效頻率
當頻率處于電容自諧振點以上時,電容的阻抗可近似表示為:頻率 f 越高,阻抗越大,但阻抗不能超過目標阻抗。假設 ESL 為 5nH,則最高有效頻率為:。這樣一個大的電容能夠讓我們把電源阻抗在 100kHz 到1.6MHz 之間控制在目標阻抗之下。當頻率高于 1.6MHz 時,還需要額外的電容來控制電源系統阻抗。
第五步:計算頻率高于 1.6MHz 時所需電容
如果希望電源系統在 500MHz 以下時都能滿足電壓波動要求,就必須控制電容的寄生電感量。必須滿足
所以有:
假設使用 AVX 公司的 0402 封裝陶瓷電容,寄生電感約為 0.4nH,加上安裝到電路板上后過孔的寄生電感(本文后面有計算方法)假設為 0.6nH,則總的寄生電感為 1 nH。為了滿足總電感不大于 0.16 nH 的要求,我們需要并聯的電容個數為:1/0.016=62.5 個,因此需要 63 個 0402 電容。
為了在 1.6MHz 時阻抗小于目標阻抗,需要電容量為:
因此每個電容的電容量為 1.9894/63=0.0316 uF。
綜上所述,對于這個系統,我們選擇 1 個 31.831 uF 的大電容和 63 個 0.0316 uF 的小電容即可滿足要求。
相同容值電容的并聯
使用很多電容并聯能有效地減小阻抗。63 個 0.0316 uF 的小電容(每個電容 ESL 為 1 nH)并聯的效果相當于一個具有 0.159 nH ESL 的 1.9908 uF 電容。
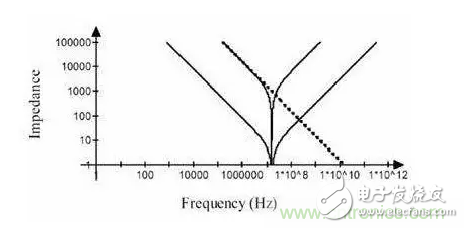
圖 10 多個等值電容并聯
單個電容及并聯電容的阻抗特性如圖 10 所示。并聯后仍有相同的諧振頻率,但是并聯電容在每一個頻率點上的阻抗都小于單個電容。
但是,從圖中我們看到,阻抗曲線呈 V 字型,隨著頻率偏離諧振點,其阻抗仍然上升的很快。要在很寬的頻率范圍內滿足目標阻抗要求,需要并聯大量的同值電容。這不是一種好的方法,造成極大地浪費。有些人喜歡在電路板上放置很多 0.1uF 電容,如果你設計的電路工作頻率很高,信號變化很快,那就不要這樣做,最好使用不同容值的組合來構成相對平坦的阻抗曲線。
不同容值電容的并聯與反諧振(Anti-Resonance)
容值不同的電容具有不同的諧振點。圖 11 畫出了兩個電容阻抗隨頻率變化的曲線。
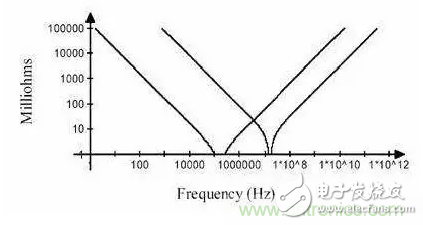
圖 11 兩個不同電容的阻抗曲線
左邊諧振點之前,兩個電容都呈容性,右邊諧振點后,兩個電容都呈感性。在兩個諧振點之間,阻抗曲線交叉,在交叉點處,左邊曲線代表的電容呈感性,而右邊曲線代表的電容呈容性,此時相當于 LC 并聯電路。對于 LC 并聯電路來說,當 L 和 C 上的電抗相等時,發生并聯諧振。因此,兩條曲線的交叉點處會發生并聯諧振,這就是反諧振效應,該頻率點為反諧振點。
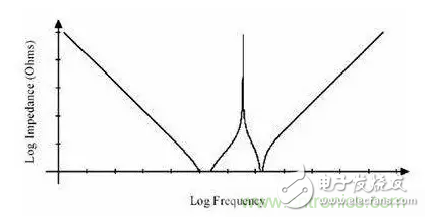
圖 12 不同容值電容并聯后阻抗曲線
兩個容值不同的電容并聯后,阻抗曲線如圖 12 所示。從圖 12 中我們可以得出兩個結論:
a 不同容值的電容并聯,其阻抗特性曲線的底部要比圖 10 阻抗曲線的底部平坦得多(雖然存在反諧振點,有一個阻抗尖峰),因而能更有效地在很寬的頻率范圍內減小阻抗。
b 在反諧振(Anti-Resonance)點處,并聯電容的阻抗值無限大,高于兩個電容任何一個單獨作用時的阻抗。并聯諧振或反諧振現象是使用并聯去耦方法的不足之處。在并聯電容去耦的電路中,雖然大多數頻率值的噪聲或信號都能在電源系統中找到低阻抗回流路徑,但是對于那些頻率值接近反諧振點的,由于電源系統表現出的高阻抗,使得這部分噪聲或信號能量無法在電源分配系統中找到回流路徑,最終會從 PCB 上發射出去(空氣也是一種介質,波阻抗只有幾百歐姆),從而在反諧振頻率點處產生嚴重的 EMI 問題。
因此,并聯電容去耦的電源分配系統一個重要的問題就是:合理的選擇電容,盡可能的壓低反諧振點處的阻抗。
ESR 對反諧振(Anti-Resonance)的影響Anti-Resonance 給電源去耦帶來麻煩,但幸運的是,實際情況不會像圖 12 顯示的那么糟糕。
實際電容除了 LC 之外,還存在等效串聯電阻 ESR。
因此,反諧振點處的阻抗也不會是無限大的。實際上,可以通過計算得到反諧振點處的阻抗,X 為反諧振點處單個電容的阻抗虛部(均相等)。
