完善資料讓更多小伙伴認(rèn)識你,還能領(lǐng)取20積分哦,立即完善>
標(biāo)簽 > 小波變換
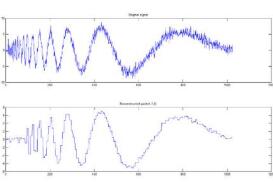
小波變換是一種新的變換分析方法,它繼承和發(fā)展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等缺點(diǎn),能夠提供一個隨頻率改變的“時間-頻率”窗口,是進(jìn)行信號時頻分析和處理的理想工具。
小波變換(wavelet transform,WT)是一種新的變換分析方法,它繼承和發(fā)展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等缺點(diǎn),能夠提供一個隨頻率改變的“時間-頻率”窗口,是進(jìn)行信號時頻分析和處理的理想工具。它的主要特點(diǎn)是通過變換能夠充分突出問題某些方面的特征,能對時間(空間)頻率的局部化分析,通過伸縮平移運(yùn)算對信號(函數(shù))逐步進(jìn)行多尺度細(xì)化,最終達(dá)到高頻處時間細(xì)分,低頻處頻率細(xì)分,能自動適應(yīng)時頻信號分析的要求,從而可聚焦到信號的任意細(xì)節(jié),解決了Fourier變換的困難問題,成為繼Fourier變換以來在科學(xué)方法上的重大突破。
傳統(tǒng)的信號理論,是建立在Fourier分析基礎(chǔ)上的,而Fourier變換作為一種全局性的變化,其有一定的局限性,如不具備局部化分析能力、不能分析非平穩(wěn)信號等。在實(shí)際應(yīng)用中人們開始對Fourier變換進(jìn)行各種改進(jìn),以改善這種局限性,如STFT(短時傅立葉變換)。由于STFT采用的的滑動窗函數(shù)一經(jīng)選定就固定不變,故決定了其時頻分辨率固定不變,不具備自適應(yīng)能力,而小波分析很好的解決了這個問題。小波分析是一種新興的數(shù)學(xué)分支,它是泛函數(shù)、Fourier分析、調(diào)和分析、數(shù)值分析的最完美的結(jié)晶;在應(yīng)用領(lǐng)域,特別是在信號處理、圖像處理、語音處理以及眾多非線性科學(xué)領(lǐng)域,它被認(rèn)為是繼Fourier分析之后的又一有效的時頻分析方法。小波變換與Fourier變換相比,是一個時間和頻域的局域變換因而能有效地從信號中提取信息,通過伸縮和平移等運(yùn)算功能對函數(shù)或信號進(jìn)行多尺度細(xì)化分析(Multiscale Analysis),解決了Fourier變換不能解決的許多困難問題。
小波變換(wavelet transform,WT)是一種新的變換分析方法,它繼承和發(fā)展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等缺點(diǎn),能夠提供一個隨頻率改變的“時間-頻率”窗口,是進(jìn)行信號時頻分析和處理的理想工具。它的主要特點(diǎn)是通過變換能夠充分突出問題某些方面的特征,能對時間(空間)頻率的局部化分析,通過伸縮平移運(yùn)算對信號(函數(shù))逐步進(jìn)行多尺度細(xì)化,最終達(dá)到高頻處時間細(xì)分,低頻處頻率細(xì)分,能自動適應(yīng)時頻信號分析的要求,從而可聚焦到信號的任意細(xì)節(jié),解決了Fourier變換的困難問題,成為繼Fourier變換以來在科學(xué)方法上的重大突破。
傳統(tǒng)的信號理論,是建立在Fourier分析基礎(chǔ)上的,而Fourier變換作為一種全局性的變化,其有一定的局限性,如不具備局部化分析能力、不能分析非平穩(wěn)信號等。在實(shí)際應(yīng)用中人們開始對Fourier變換進(jìn)行各種改進(jìn),以改善這種局限性,如STFT(短時傅立葉變換)。由于STFT采用的的滑動窗函數(shù)一經(jīng)選定就固定不變,故決定了其時頻分辨率固定不變,不具備自適應(yīng)能力,而小波分析很好的解決了這個問題。小波分析是一種新興的數(shù)學(xué)分支,它是泛函數(shù)、Fourier分析、調(diào)和分析、數(shù)值分析的最完美的結(jié)晶;在應(yīng)用領(lǐng)域,特別是在信號處理、圖像處理、語音處理以及眾多非線性科學(xué)領(lǐng)域,它被認(rèn)為是繼Fourier分析之后的又一有效的時頻分析方法。小波變換與Fourier變換相比,是一個時間和頻域的局域變換因而能有效地從信號中提取信息,通過伸縮和平移等運(yùn)算功能對函數(shù)或信號進(jìn)行多尺度細(xì)化分析(Multiscale Analysis),解決了Fourier變換不能解決的許多困難問題。
小波分析
與Fourier變換相比,小波變換是空間(時間)和頻率的局部變換,因而能有效地從信號中提取信息。通過伸縮和平移等運(yùn)算功能可對函數(shù)或信號進(jìn)行多尺度的細(xì)化分析,解決了Fourier變換不能解決的許多困難問題。小波變換聯(lián)系了應(yīng)用數(shù)學(xué)、物理學(xué)、計算機(jī)科學(xué)、信號與信息處理、圖像處理、地震勘探等多個學(xué)科。數(shù)學(xué)家認(rèn)為,小波分析是一個新的數(shù)學(xué)分支,它是泛函分析、Fourier分析、樣條分析、數(shù)值分析的完美結(jié)晶;信號和信息處理專家認(rèn)為,小波分析是時間—尺度分析和多分辨分析的一種新技術(shù),它在信號分析、語音合成、圖像識別、計算機(jī)視覺、數(shù)據(jù)壓縮、地震勘探、大氣與海洋波分析等方面的研究都取得了有科學(xué)意義和應(yīng)用價值的成果。信號分析的主要目的是尋找一種簡單有效的信號變換方法,使信號所包含的重要信息能顯現(xiàn)出來。小波分析屬于信號時頻分析的一種,在小波分析出現(xiàn)之前,傅立葉變換是信號處理領(lǐng)域應(yīng)用最廣泛、效果最好的一種分析手段。傅立葉變換是時域到頻域互相轉(zhuǎn)化的工具,從物理意義上講,傅立葉變換的實(shí)質(zhì)是把這個波形分解成不同頻率的正弦波的疊加和。正是傅立葉變換的這種重要的物理意義,決定了傅立葉變換在信號分析和信號處理中的獨(dú)特地位。傅立葉變換用在兩個方向上都無限伸展的正弦曲線波作為正交基函數(shù),把周期函數(shù)展成傅立葉級數(shù),把非周期函數(shù)展成傅立葉積分,利用傅立葉變換對函數(shù)作頻譜分析,反映了整個信號的時間頻譜特性,較好地揭示了平穩(wěn)信號的特征。
小波變換是一種新的變換分析方法,它繼承和發(fā)展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等缺點(diǎn),能夠提供一個隨頻率改變的“時間-頻率”窗口,是進(jìn)行信號時頻分析和處理的理想工具。它的主要特點(diǎn)是通過變換能夠充分突出問題某些方面的特征,因此,小波變換在許多領(lǐng)域都得到了成功的應(yīng)用,特別是小波變換的離散數(shù)字算法已被廣泛用于許多問題的變換研究中。從此,小波變換越來越引起人們的重視,其應(yīng)用領(lǐng)域來越來越廣泛。
應(yīng)用
是與小波分析的理論研究緊密地結(jié)合在一起的。現(xiàn)在,它已經(jīng)在科技信息產(chǎn)業(yè)領(lǐng)域取得了令人矚目的成就。電子信息技術(shù)是六大高新技術(shù)中重要的一個領(lǐng)域,它的重要方面是圖象和信號處理。現(xiàn)今,信號處理已經(jīng)成為當(dāng)代科學(xué)技術(shù)工作的重要部分,信號處理的目的就是:準(zhǔn)確的分析、診斷、編碼壓縮和量化、快速傳遞或存儲、精確地重構(gòu)(或恢復(fù))。從數(shù)學(xué)地角度來看,信號與圖象處理可以統(tǒng)一看作是信號處理(圖象可以看作是二維信號),小波分析的許多分析和應(yīng)用問題,都可以歸結(jié)為信號處理問題。現(xiàn)在,對于其性質(zhì)隨時間是穩(wěn)定不變的信號(平穩(wěn)隨機(jī)過程),處理的理想工具仍然是傅立葉分析。但是在實(shí)際應(yīng)用中的絕大多數(shù)信號是非穩(wěn)定的(非平穩(wěn)隨機(jī)過程),而特別適用于非穩(wěn)定信號的工具就是小波分析。
事實(shí)上小波分析的應(yīng)用領(lǐng)域十分廣泛,它包括:數(shù)學(xué)領(lǐng)域的許多學(xué)科;信號分析、圖象處理;量子力學(xué)、理論物理;軍事電子對抗與武器的智能化;計算機(jī)分類與識別;音樂與語言的人工合成;醫(yī)學(xué)成像與診斷;地震勘探數(shù)據(jù)處理;大型機(jī)械的故障診斷等方面;例如,在數(shù)學(xué)方面,它已用于數(shù)值分析、構(gòu)造快速數(shù)值方法、曲線曲面構(gòu)造、微分方程求解、控制論等。在信號分析方面的濾波、去噪聲、壓縮、傳遞等。在圖象處理方面的圖象壓縮、分類、識別與診斷,去污等。在醫(yī)學(xué)成像方面的減少B超、CT、核磁共振成像的時間,提高分辨率等。
⑴小波分析用于信號與圖象壓縮是小波分析應(yīng)用的一個重要方面。它的特點(diǎn)是壓縮比高,壓縮速度快,壓縮后能保持信號與圖象的特征不變,且在傳遞中可以抗干擾。基于小波分析的壓縮方法很多,比較成功的有小波包最好基方法,小波域紋理模型方法,小波變換零樹壓縮,小波變換向量壓縮等。
⑵小波在信號分析中的應(yīng)用也十分廣泛。它可以用于邊界的處理與濾波、時頻分析、信噪分離與提取弱信號、求分形指數(shù)、信號的識別與診斷以及多尺度邊緣檢測等。
⑶在工程技術(shù)等方面的應(yīng)用。包括計算機(jī)視覺、計算機(jī)圖形學(xué)、曲線設(shè)計、湍流、遠(yuǎn)程宇宙的研究與生物醫(yī)學(xué)方面。
從圖像處理的角度看,小波變換存在以下幾個優(yōu)點(diǎn):
⑴小波分解可以覆蓋整個頻域(提供了一個數(shù)學(xué)上完備的描述)⑵小波變換通過選取合適的濾波器,可以極大的減小或去除所提取得不同特征之間的相關(guān)性⑶小波變換具有“變焦”特性,在低頻段可用高頻率分辨率和低時間分辨率(寬分析窗口),在高頻段,可用低頻率分辨率和高時間分辨率(窄分析窗口)⑷小波變換實(shí)現(xiàn)上有快速算法(Mallat小波分解算法)
能不能通俗的講解下傅立葉分析和小波分析之間的關(guān)系
小波,一個神奇的波,可長可短可胖可瘦(伸縮平移),當(dāng)去學(xué)習(xí)小波的時候,第一個首先要做的就是回顧傅立葉變換(又回來了,唉),因?yàn)樗麄兌际穷l率變換的方法,而傅立葉變換是最入門的,也是最先了解的,通過傅立葉變換,了解缺點(diǎn),改進(jìn),慢慢的就成了小波變換。主要的關(guān)鍵的方向是傅立葉變換、短時傅立葉變換,小波變換等,第二代小波的什么的就不說了,太多了沒太多意義。當(dāng)然,其中會看到很多的名詞,例如,內(nèi)積,基,歸一化正交,投影,Hilbert空間,多分辨率,父小波,母小波,這些不同的名詞也是學(xué)習(xí)小波路上的標(biāo)志牌,所以在剛學(xué)習(xí)小波變換的時候,看著三個方向和標(biāo)志牌,可以順利的走下去,當(dāng)然路上的美景要自己去欣賞(這里的美景就是定義和推導(dǎo)了)。因?yàn)閮?nèi)容太多,不是很重要的地方我都注釋為(查定義)一堆文字的就是理論(可以大體一看不用立刻就懂),同時最下面也給了幾個網(wǎng)址輔助學(xué)習(xí)。
一、基
傅立葉變換和小波變換,都會聽到分解和重構(gòu),其中這個就是根本,因?yàn)樗麄兊淖兓际菍⑿盘柨闯捎扇舾蓚€東西組成的,而且這些東西能夠處理還原成比原來更好的信號。那怎么分解呢?那就需要一個分解的量,也就是常說的基,基的了解可以類比向量,向量空間的一個向量可以分解在x,y方向,同時在各個方向定義單位向量e1、e2,這樣任意一個向量都可以表示為a=xe1+ye2,這個是二維空間的基,
而對于傅立葉變換的基是不同頻率的正弦曲線,所以傅立葉變換是把信號波分解成不同頻率的正弦波的疊加和,而對于小波變換就是把一個信號分解成一系列的小波,這里時候,也許就會問,小波變換的小波是什么啊,定義中就是告訴我們小波,因?yàn)檫@個小波實(shí)在是太多,一個是種類多,還有就是同一種小波還可以尺度變換,但是小波在整個時間范圍的幅度平均值是0,具有有限的持續(xù)時間和突變的頻率和振幅,可以是不規(guī)則,也可以是不對稱,很明顯正弦波就不是小波,什么的是呢,看下面幾個圖就是

當(dāng)有了基,以后有什么用呢?
下面看一個傅立葉變換的實(shí)例:
對于一個信號的表達(dá)式為x=sin(2*pi*t)+0.5*sin(2*pi*5*t);
這里可以看到是他的基就是sin函數(shù),頻率是1和5,下面看看圖形的表示,是不是感受了到了頻域變換給人的一目了然。
基具有非冗余性,即使基不是正交的,有相關(guān)性,但若去掉其中任何一個,則不成為基,這一點(diǎn)也叫完備性;基的表示有唯一性,即給定一族基對一個函數(shù)的表達(dá)是唯一的;一般情況下基非正交,也稱為為exact frame(Resize basis),這個時候要表示信號可以將基正交化成唯一的正交基(對偶為其自身);也可以求其對偶框架(dual frame),其對應(yīng)了小波變換中的雙正交情形!信號可以依框架分解,然后用對偶框架重構(gòu)。若在基集里添加一些新的向量,并隨意調(diào)整空間位置,則有可能成為框架。把函數(shù)與基或框架作內(nèi)積,也可以說成是一種函數(shù)空間到系數(shù)空間的變換。若某種變換后的能量(內(nèi)積的平方和度量)仍然有一個大于0的上下界,才可以成為框架,由于框架的冗余性,所以系數(shù)的表達(dá)也不具有唯一性。若上下界相等,則為緊框架,且界表示冗余度。若上下界相等為且為1,稱為pasval identity frame,此時不一定為正交基(想象把一組正交基中某一個拆成兩個同方向的基之和,則pasval identity仍然成立),此時若加上基的長度均為一的條件,則框架退化為正交基。可能你會問我們用基來表示信號就行了啊,為什么還要框架呢?其實(shí)很多信號表示方法不能構(gòu)成基,卻能構(gòu)成框架,如短時傅立葉變換中如要求窗函數(shù)滿足基條件,則可推出該函數(shù)有很差的時頻局部化性質(zhì)(事實(shí)上退化為了傅立葉變換。
二、內(nèi)積
在Hilbert空間(查定義)里看到這個東西,用來刻畫兩個向量的夾角,當(dāng)內(nèi)積為0時,兩個向量正交,若g為Hilbert空間里的正交基的時候,內(nèi)積為f向基上的正交投影;(Hilbert空間是一個很直觀的空間,我一直都理解為歐氏空間去理解定義在其上的東西,L^2(平方可積,查定義)和l^2同樣為Hilbert空間。
下面這個公式是基本,經(jīng)過變形后會用在推導(dǎo)中:
如果兩個向量的內(nèi)積為0 ,就說他們是正交的。
如果一個向量序列相互對偶正交,并且長度都為1,那么就說他們是正交歸一化的。
對于,存在L2(R)上一組標(biāo)準(zhǔn)正交基gi(t),i=1,2,3…。,使得
L2(R)上任意一個函數(shù)f(t)都可以由L2(R)上的一個規(guī)范正交基gi(t)進(jìn)行線性組合表示出來
三、傅立葉的缺點(diǎn)
先列舉出來缺點(diǎn),然后再說明:
(1) Fourier分析不能刻畫時間域上信號的局部特性
(2) Fourier分析對突變和非平穩(wěn)信號的效果不好,沒有時頻分析
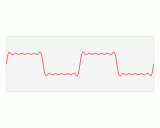
傅立葉變換傅立葉變換將函數(shù)投影到三角波上,將函數(shù)分解成了不同頻率的三角波,這不能不說是一個偉大的發(fā)現(xiàn),但是在大量的應(yīng)用中,傅立葉變換的局限性卻日趨明顯,事實(shí)上在光滑平穩(wěn)信號的表示中,傅立葉基已經(jīng)達(dá)到了近似最優(yōu)表示,但是日常生活中的信號卻并不是一直光滑的,而且奇異是平凡的,傅立葉在奇異點(diǎn)的表現(xiàn)就著實(shí)讓人不爽,從對方波的傅立葉逼近就可以看出來,用了大量不同頻率的三角波去逼近其系數(shù)衰減程度相當(dāng)緩慢,而且會產(chǎn)生Gibbs效應(yīng)。其內(nèi)在的原因是其基為全局性基,沒有局部化能力,以至局部一個小小的擺動也會影響全局的系數(shù)。實(shí)際應(yīng)用中很需要時頻局部化,傅立葉顯然缺乏此能力了。即使如此,由于其鮮明的物理意義和快速計算,在很多場合仍然應(yīng)用廣泛。傅立葉變換在從連續(xù)到離散的情形是值得借鑒與學(xué)習(xí)的,大家都知道,時間周期對應(yīng)頻域離散,時間離散對應(yīng)頻域周期,時間離散周期對應(yīng)頻域離散 周期,DFT其實(shí)是將離散信號做周期延拓然后做傅立葉變換再截取一個周期,反變換同樣如此,所以DFT用的是塊基的概念,這樣如果信號兩端的信號連接后不再光滑(即使兩邊都光滑),同樣會在邊界上產(chǎn)生大幅值系數(shù)(邊界效應(yīng)),延伸到圖像中就是塊效應(yīng)。當(dāng)對信號做對稱周期延拓后再做傅立葉變換得到的正弦系數(shù)全部為0,也就是任何對稱函數(shù)可以寫成余弦的線性組合,同樣按照離散的思路構(gòu)造得到的是離散塊余弦基,即DCT變換,雖然DCT可以通過對稱后周期延拓再變換減少了邊界效應(yīng)(兩邊信號接上了,但不一定平滑),但任不能消除塊效應(yīng),尤其是圖像變換中人為將圖像分成8*8處理后塊效應(yīng)更加明顯。但是DCT很好的能量聚集效應(yīng)讓人驚奇,加之快速計算方法使它替代DFT成為圖像的壓縮的標(biāo)準(zhǔn)了很長時間(JPEG)。
上面一堆文字也許看的有點(diǎn)蒙,還是用圖來說明
第一個就是傅立葉變換是整個時域,所以沒有局部特征,這個也是他的基函數(shù)決定的看圖,同時如果在時域張有了突變,那么在頻域就需要大量的三角波去擬合,這也是傅立葉變換性質(zhì)決定的。
第二個就是面對非平穩(wěn)信號,傅立葉變換可以看到由哪些頻域組成,但是不知道各成分對應(yīng)的時刻是什么,也就是沒有時頻分析,看不出來信號頻域隨著時間變換的情況,反過來說就是,一個的頻圖對應(yīng)好幾個時域圖,不知道是哪個,這個在實(shí)際應(yīng)用中就不好了,看圖
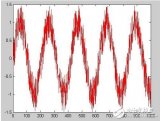
做FFT后,我們發(fā)現(xiàn)這三個時域上有巨大差異的信號,頻譜(幅值譜)卻非常一致。尤其是下邊兩個非平穩(wěn)信號,我們從頻譜上無法區(qū)分它們,因?yàn)樗鼈儼乃膫€頻率的信號的成分確實(shí)是一樣的,只是出現(xiàn)的先后順序不同。
可見,傅里葉變換處理非平穩(wěn)信號有天生缺陷。它只能獲取一段信號總體上包含哪些頻率的成分,但是對各成分出現(xiàn)的時刻并無所知。因此時域相差很大的兩個信號,可能頻譜圖一樣。
然而平穩(wěn)信號大多是人為制造出來的,自然界的大量信號幾乎都是非平穩(wěn)的,所以在比如生物醫(yī)學(xué)信號分析等領(lǐng)域的論文中,基本看不到單純傅里葉變換這樣naive的方法。
上圖所示的是一個正常人的事件相關(guān)電位。對于這樣的非平穩(wěn)信號,只知道包含哪些頻率成分是不夠的,我們還想知道各個成分出現(xiàn)的時間。知道信號頻率隨時間變化的情況,各個時刻的瞬時頻率及其幅值——這也就是時頻分析。
三、短時傅立葉變換(Short-time Fourier Transform,STFT)
有了缺點(diǎn)就要改進(jìn)了,這里就出來了短時傅立葉變換,也叫加窗傅立葉變換,顧名思義,就是因?yàn)楦盗⑷~變換的時域太長了,所以要弄短一點(diǎn),這樣就有了局部性。
定義:把整個時域過程分解成無數(shù)個等長的小過程,每個小過程近似平穩(wěn),再傅里葉變換,就知道在哪個時間點(diǎn)上出現(xiàn)了什么頻率了。”這就是短時傅里葉變換。下面就是示意圖
時域上分成一段一段做FFT,不就知道頻率成分隨著時間的變化情況了嗎!
可能理解這一點(diǎn)最好的方式是舉例子。首先,因?yàn)槲覀兊淖儞Q是對時間和頻率的函數(shù)(不像傅立葉變換,僅僅是對頻率的函數(shù)),它是二維的(如果加上幅度則是三維)。以下圖所示的非平穩(wěn)信號為例:
在這個信號中,在不同時刻有四個頻率分量。0-250ms內(nèi)信號的頻率為300Hz,其余每個250ms的間隔的信號頻率分別為200Hz,100Hz和50Hz。很明顯,這是一個非平穩(wěn)信號,讓我們看一看它的短時傅立葉變換:用這樣的方法,可以得到一個信號的時頻圖了:
圖上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四個頻域成分,還能看到出現(xiàn)的時間。兩排峰是對稱的,所以大家只用看一排就行了。
看著貌似解決了問題,好像有了局部性,但是這個名字叫做加窗傅立葉變換,那么這個窗要多大了呢?
窗太窄,窗內(nèi)的信號太短,會導(dǎo)致頻率分析不夠精準(zhǔn),頻率分辨率差。
窗太寬,時域上又不夠精細(xì),時間分辨率低。
(這里插一句,這個道理可以用海森堡不確定性原理來解釋。類似于我們不能同時獲取一個粒子的動量和位置,我們也不能同時獲取信號絕對精準(zhǔn)的時刻和頻率。這也是一對不可兼得的矛盾體。我們不知道在某個瞬間哪個頻率分量存在,我們知道的只能是在一個時間段內(nèi)某個頻帶的分量存在。所以絕對意義的瞬時頻率是不存在的。)
上圖對同一個信號(4個頻率成分)采用不同寬度的窗做STFT,結(jié)果如右圖。用窄窗,時頻圖在時間軸上分辨率很高,幾個峰基本成矩形,而用寬窗則變成了綿延的矮山。但是頻率軸上,窄窗明顯不如下邊兩個寬窗精確。
所以窄窗口時間分辨率高、頻率分辨率低,寬窗口時間分辨率低、頻率分辨率高。
對于時變的非穩(wěn)態(tài)信號,高頻適合小窗口,低頻適合大窗口。然而STFT的窗口是固定的,在一次STFT中寬度不會變化,所以STFT還是無法滿足非穩(wěn)態(tài)信號變化的頻率的需求。
四、小波變換
真是千呼萬喚才出來了,終于看見小波了啊。
這里先引入小波,回顧一下基,然后再看看小波的優(yōu)點(diǎn),其實(shí)就是上面傅立葉缺點(diǎn)的解決。
對于加窗傅立葉變換讓人頭疼的就是窗口的大小問題,如果我們讓窗口的大小可以改變,不就完美了嗎?答案是肯定的,小波就是基于這個思路,但是不同的是。STFT是給信號加窗,分段做FFT;而小波變換并沒有采用窗的思想,更沒有做傅里葉變換。小波直接把傅里葉變換的基給換了——將無限長的三角函數(shù)基換成了有限長的會衰減的小波基。這樣不僅能夠獲取頻率,還可以定位到時間了~
這里就又回到了最開始的基了。
這個基函數(shù)會伸縮、會平移(其實(shí)是兩個正交基的分解)。縮得窄,對應(yīng)高頻;伸得寬,對應(yīng)低頻。然后這個基函數(shù)不斷和信號做相乘。某一個尺度(寬窄)下乘出來的結(jié)果,就可以理解成信號所包含的當(dāng)前尺度對應(yīng)頻率成分有多少。于是,基函數(shù)會在某些尺度下,與信號相乘得到一個很大的值,因?yàn)榇藭r二者有一種重合關(guān)系。那么我們就知道信號包含該頻率的成分的多少。如前邊所說,小波做的改變就在于,將無限長的三角函數(shù)基換成了有限長的會衰減的小波基。效果如下圖
現(xiàn)在來看一下小波公式
從公式可以看出,不同于傅里葉變換,變量只有頻率ω,小波變換有兩個變量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函數(shù)的伸縮,平移量 τ控制小波函數(shù)的平移。尺度就對應(yīng)于頻率(反比),平移量 τ就對應(yīng)于時間。如下圖
當(dāng)伸縮、平移到這么一種重合情況時,也會相乘得到一個大的值。這時候和傅里葉變換不同的是,這不僅可以知道信號有這樣頻率的成分,而且知道它在時域上存在的具體位置。
而當(dāng)我們在每個尺度下都平移著和信號乘過一遍后,我們就知道信號在每個位置都包含哪些頻率成分。
看到了嗎?有了小波,我們從此再也不害怕非穩(wěn)定信號啦!從此可以做時頻分析啦!
(1) 解決了局部性
(2)解決時頻分析
做傅里葉變換只能得到一個頻譜,做小波變換卻可以得到一個時頻譜!

時域信號 傅立葉變換結(jié)果 小波變換結(jié)果
五、小波的深入
上面那么多,也就是走進(jìn)小波的大門,具體的我們還要學(xué)習(xí)子空間、多分辨率,母小波的變換,如何去構(gòu)造想要的小波函數(shù),然后還有離散小波變換,正交小波變換,二維小波變換,小波包的應(yīng)用(這里沒有介紹可以自己看資料)。好像還有很多要學(xué)習(xí)的。
這里先深入一下,父小波和母小波,多分辨率分析,了解一下伸縮和平移。
任何小波變換的基函數(shù),其實(shí)就是對母小波和父小波縮放和平移的集合。首先要看的就是多分辨率分析。
每個小波變換都會有一個mother wavelet,我們稱之為母小波,同時還有一個father wavelet,就是scaling function。而該小波的basis函數(shù)其實(shí)就是對這個母小波和父小波縮放和平移形成的。縮放倍數(shù)都是2的級數(shù),平移的大小和當(dāng)前其縮放的程度有關(guān)。
還講到,小波系統(tǒng)有很多種,不同的母小波,衍生的小波基就完全不同。小波展開的近似形式是這樣:
其中的就是小波級數(shù),這些級數(shù)的組合就形成了小波變換中的基basis。和傅立葉級數(shù)有一點(diǎn)不同的是,小波級數(shù)通常是orthonormal basis,也就是說,它們不僅兩兩正交,還歸一化了。
我們還講了一般小波變換的三個特點(diǎn),就是小波級數(shù)是二維的,能定位時域和頻域,計算很快。但我們并沒有深入講解,比如,如何理解這個二維?它是如何同時定位頻域和時域的?
在這一篇文章里,我們就來討論一下這些特性背后的原理。
首先,我們一直都在講小波展開的近似形式。那什么是完整形式呢?之前講到,小波basis的形成,是基于基本的小波函數(shù),也就是母小波來做縮放和平移的。但是,母小波并非唯一的原始基。在構(gòu)建小波基函數(shù)集合的時候,通常還要用到一個函數(shù)叫尺度函數(shù),scaling function,人們通常都稱其為父小波。它和母小波一樣,也是歸一化了,而且它還需要滿足一個性質(zhì),就是它和對自己本身周期平移的函數(shù)兩兩正交:
另外,為了方便處理,父小波和母小波也需要是正交的。可以說,完整的小波展開就是由母小波和父小波共同定義的。
其中ψ(t)是母小波,是父小波。需要提醒一點(diǎn)的是,這個正交純粹是為了小波分析的方便而引入的特性,并不是說小波變換的基就一定必須是正交的。但大部分小波變換的基確實(shí)是正交的,所以本文就直接默認(rèn)正交為小波變換的主要性質(zhì)之一了。引入這個父小波呢,主要是為了方便做多解析度分析(multiresolution analysis, MRA)。說到這里,你的問題可能會井噴了:好好的為什么出來一個父小波呢?這個scaling function是拿來干嘛的?它背后的物理意義是什么?waveletfunction背后的物理意義又是什么?這個多解析度分析又是什么呢?不急,下面,我們圍繞一個例子來鞏固一下前面的知識,同時再引出新的特性。
假設(shè)我們有這樣一個信號:
該信號長度為8,是離散的一維信號。我們要考慮的,就是如何用小波將其展開。為了方便講解,我們考慮最簡單的一種小波,哈爾小波。下面是它的一種母小波:
那如何構(gòu)建基于這個母小波的基呢?剛才提到了,要縮放,要平移。我們先試試縮放,那就是ψ(2n):
但這樣的話,它與自己的內(nèi)積就不是1了,不符合小波基orthonormal的要求,所以我們要在前面加一個系數(shù)根號二,這樣我們就得到了另一個哈爾小波的basis function:
同理,我們可以一直這樣推廣下去做scale,得到4n,8n,……。下的basis function。當(dāng)然在這個例子里,我們信號長度就是8,所以做到4n就夠了。但推廣來說,就是這種scaling對母小波的作用為,這是歸一化后的表示形式。
平移的話也很簡單,我們可以對母小波進(jìn)行平移,也可以對scale之后的basis function進(jìn)行平移。比如對上一幅圖中的basis function進(jìn)行平移,就成了
看得出來,平移后的basis function和母小波以及僅僅scale過的小波,都是正交的,附合小波basis的特點(diǎn)。如果我們用ψ(n)來表示這個mother wavelet,那么這些orthonormal basis函數(shù)可以寫成:
這里的k是可以看成時域的參數(shù),因?yàn)樗刂浦〔ɑ鶗r域的轉(zhuǎn)移,而j是頻域的參數(shù),因?yàn)樗鼪Q定了小波基的頻率特性。看到這里,你應(yīng)該會感覺很熟悉,因?yàn)檫@里的平移和變換本質(zhì)和剛才對scaling function的平移變換是一模一樣的。
這樣,我們就有了針對此信號space的哈爾小波basis組合:
可以看出,我們用到了三層頻率尺度的小波函數(shù),每往下一層,小波的數(shù)量都是上面一層的兩倍。在圖中,每一個小波基函數(shù)的表達(dá)形式都寫在了波形的下面。
等等,你可能已經(jīng)發(fā)現(xiàn)了,有問題。這里為什么多了個沒有函數(shù)表達(dá)式的波形呢?這貨明顯不是wavelet function阿。沒錯,它是之前提到的scaling function,也就是父小波。然后你可能就會問,為啥這個憑空插了一個scaling function出來呢?明明目標(biāo)信號已經(jīng)可以用純的小波基組合表示了。是,確實(shí)是,就算不包括scaling function,這些小波函數(shù)本身也組成了正交歸一基,但如果僅限于此的話,小波變換也就沒那么神奇的功效了。引入這個scaling function,才能引入我們提到的多解析度分析的理論,而小波變換的強(qiáng)大,就體現(xiàn)在這個多解析度上。那在這里,我們怎么用這個多解析度呢?這個哈爾小波basis組合是怎么通過多解析度推導(dǎo)出來的呢?
話說在數(shù)學(xué)定義中,有一種空間叫Lebesgue空間,對于信號處理非常重要,可以用L^p(R)表示,指的是由p次可積函數(shù)所組成的函數(shù)空間。我們在小波變換中要研究的信號都是屬于L^2(R)空間的,這個空間是R上的所有處處平方可積的可測函數(shù)的集合,這樣就等于對信號提出了一個限制,就是信號能量必須是有限的,否則它就不可積了。小波變換的定義都是基于但不限于L^2(R)中的信號的。這玩意的特性要具體解釋起來太數(shù)學(xué)了,牽涉到太多泛函知識,我就不在這里詳述了。而且老實(shí)說我也沒能力完全講清楚,畢竟不是學(xué)這個的,有興趣可以參考wiki。總之你記住,小波變換研究中所使用的信號基本都是平方可積的信號,但其應(yīng)用不限于這種信號,就行了。
對L^2(R)空間做MRA是在干嘛呢?就是說,在L^2(R)空間中,我們可以找出一個嵌套的空間序列,并有下列性質(zhì):
我來簡單解釋一下這些性質(zhì)。這個V_j都是L^2(R)空間中的子空間,然后他們是由小到大的,交集是{0},因?yàn)檫@是最小的子空間,并集就是L空間。是不是有點(diǎn)難以理解?沒關(guān)系,看看下面這個圖就清楚了:
這個圖是圈圈套圈圈,最里面的圈是V0,之后分別是V1,V2,V3,V4 。那他們有趣的性質(zhì)就是,假如有一個函數(shù)f(t)他屬于一個某空間,那你將其在時域上平移,它還是屬于這個空間。但如果你對它頻域的放大或縮小,它就會相應(yīng)移到下一個或者上一個空間了。
同時我們還知道,你要形容每一個空間的話,都需要有對應(yīng)的orthonormal basis,這是必然的,那對于V0來講,它的orthonormal basis就是
這一系列函數(shù)是什么呢?是的時域變換,而且我們剛才也說了,時域上平移,是不會跳出這個空間的。這樣,我們就可以說,由這一系列basis所定義的L^2(R)子空間V0被這些basis所span,表示成:
k從負(fù)無窮到正無窮。上面的bar表示這是一個閉包空間,也就是說
這樣,我們就定義了基本的V0這個子空間。剛才說了,這個子空間的基都是對的整數(shù)時域變換,這里我們稱為scalingfunction,所以換個說法,就是說這里整個子空間V0,由scalingfunction和其時域變換的兄弟們span。
當(dāng)然,如果這個scaling function只是用來代表一個子空間的,那它的地位也就不會這么重要了。剛才我們提到,這個嵌套空間序列有一個性質(zhì),。這就是這個函數(shù),如果你對它頻域的放大或縮小,它就會相應(yīng)移到下一個或者上一個空間了。這個性質(zhì)就有意思了,它代表什么呢?對于任何一個包含V0的更上一層的空間來講,他們的基都可以通過對scaling function做頻域的scale后再做時域上的整數(shù)變換得到!推廣開來就是說,當(dāng)
我們有
這也就意味著,對于任何屬于V_j空間的函數(shù)f(t),都可以表示為:
到這里,我們就明白這些個子空間和那個憑空冒出來的scaling function的作用了。scaling的構(gòu)建這些不同的子空間的基礎(chǔ),當(dāng)j越大的時候,每一次你對頻率變換后的scaling function所做的時域上的整數(shù)平移幅度會越小,這樣在這個j子空間里面得到的f(t)表示粒度會很細(xì),細(xì)節(jié)展現(xiàn)很多。反之亦然。通俗點(diǎn)說,就是對scaling function的變換平移給你不同的子空間,而不同的子空間給你不同的分辨率,這樣你就可以用不同的分辨率去看目標(biāo)信號。
下面就是時候看看什么是MRA equation了,這是更加有趣,也是更加核心的地方。通過剛才的講解,V0屬于V1,那scaling function是在V0中的,自然也在V1中了。我們把他寫成V1的基的線性組合,那就是
其中的h(n)是scaling function的系數(shù),也叫做scaling filter或者scaling vector,可以是實(shí)數(shù),也可以是虛數(shù)。根號2是為了維持norm為1的。看,在這個公式里,我們就把屬于V0的函數(shù)用V1的基表示出來了。同理,我們可以循環(huán)如此,把屬于V0的在V2,V3, …, Vn中表示出來。這些方程就是MRA equation,也叫refinement equation,它是scaling function理論的基礎(chǔ),也是小波分析的基礎(chǔ)之一。
好,稍微總結(jié)一下。到現(xiàn)在,已經(jīng)講了關(guān)于scaling function的基本理論知識,知道了信號空間可以分為不同精細(xì)度的子空間,這些子空間的basis集合就是scaling function或者頻率變換之后的scaling function,如下圖所示:
上圖就是四個子空間的basis集合的展覽。通過前面的討論,我們還知道,一開始的scalingfunction可以通過更精細(xì)的子空間的scaling function(它們都是對應(yīng)子空間的basis)來構(gòu)建。比如
對于更加finer的scale:
依此類推。實(shí)際上,對于任何scale和translate過的scaling function,都可以用更加精細(xì)的scale層面上的scaling function構(gòu)建出來。
然后,我們有各種scale下的scaling function了,該看看它們分別所對應(yīng)的嵌套的空間序列了。先看看V0,自然就是以基本的scaling function為基礎(chǔ)去span出來的:
這個不新鮮,剛才就講過了。這個子空間代表什么樣的信號?常量信號。道理很簡單,這個scaling function在整個信號長度上,沒有任何變化。繼續(xù)往下看:
這個相比V0更加finer的子空間,代表著這樣一種信號,它從1-4是常量,從5-8是另一個常量。同理我們有:
V2代表的信號,是分別在1,2; 3,4; 5,6; 7,8上有相同值的信號。那么V3呢?則表示任何信號,因?yàn)閷τ赩3來講,任何一個時間刻度上的值都可以不一樣。而且現(xiàn)在,我們也可以通過上面的一些scaling functions的波形驗(yàn)證了之前提到的多解析度分析中的一個核心性質(zhì),那就是:
我們之前講了一堆多解析度的理論,但直到現(xiàn)在,通過這些圖形化的分析,我們可能才會真正理解它。那好,既然我們有一個現(xiàn)成的信號,那就來看看,對這個信號作多解析度分析是啥樣子的:
你看,在不同的子空間,對于同一個信號就有不同的詮釋。詮釋最好的當(dāng)然是V3,完全不損失細(xì)節(jié)。這就是多解析度的意義。我們可以有嵌套的,由scalingfunction演變的basis function集合,每一個集合都提供對原始信號的某種近似,解析度越高,近似越精確。
說到這里,可能你對scaling function以及多解析度分析已經(jīng)比較理解了。但是,我們還沒有涉及到它們在小波變換中的具體應(yīng)用,也就是還沒有回答剛才那個問題:憑空插了一個scaling function到小波basis組合中干嘛。也就是說,我們希望理解scaling function是怎么和小波函數(shù)結(jié)合的呢,多解析度能給小波變換帶來什么樣的好處呢。這其實(shí)就是是小波變換中的核心知識。理解了這個,后面的小波變換就是純數(shù)學(xué)計算了。
好,我們已經(jīng)知道,對于子空間V0,basis是scalingfunction:
看出什么規(guī)律了么?多看幾次這三個圖,你會驚訝地發(fā)現(xiàn),在V0中的scaling function和wavelet function的組合,其實(shí)就是V1中的basis!繼續(xù)這樣推導(dǎo),V1本來的的basis是:
他們的組合,本質(zhì)上也就是V2的basis(參考圖2)。你繼續(xù)推導(dǎo)下去,會得到同樣的結(jié)論:在scale j的wavelet function,可以被用來將Vj的basis擴(kuò)展到V(j+1)中去!這是一個非常非常關(guān)鍵的性質(zhì),因?yàn)檫@代表著,對任何一個子空間Vj,我們現(xiàn)在有兩種方法去得到它的orthonormal basis:
1. 一種就是它本來的basis ,對任意k。
2. 第二種就是它上一個子空間的basis,對任意k,以及上一級子空間的wavelet function
,對任意k。
第二種選擇能給我們帶來額外的好處,那就是我們可以循環(huán)不斷地用上一級子空間的scaling function以及wavelet function的組合來作為當(dāng)前子空間的基。換句話說,如果針對V3這個子空間,它實(shí)際上就有四種不同的,但是等價的orthonormal basis:
1. 本級(V3)的scalingfunction basis set
2. 上一級(V2)的scalingfunction + wavelet function;
3 。 上上一級(V1)的scalingfunction + 上上一級(V1)的waveletfunction + 上一級(V2)的waveletfunction;
4. 上上上一級(V0)的scalingfunction + 上上上一級(V0)的waveletfunction + 上上一級(V1)的waveletfunction + 上一級(V2)的waveletfunction
好,看看最后一種選取方式,有沒有感到眼熟?對了,它就是我們之前提到的“針對此信號space的哈爾小波basis組合”,參見圖1。現(xiàn)在我們知道了,這個scalingfunction不是憑空插進(jìn)去的,而是通過不斷的嵌套迭代出來的:
那為什么我們最后選定的是這種選取方式呢?實(shí)際上,剛才介紹的這個性質(zhì)已經(jīng)告訴我們,對于任何的scale j0,我們都可以給我們的signal space找到一組orthonormal basis,這個basis是通過組合scale j0上的scaling function以及所有在scale j,j》=j0上的wavelets得到的。這樣,基于這個orthonormal basis,
所有信號空間中的信號都可以寫成組成這個basis的functions的線性組合:
對應(yīng)的系數(shù)的計算和平常一樣:
這,就是最終的,也是最核心的,小波變換形式。不管是信號壓縮,濾波,還是別的方式處理,只要是用小波變換,都逃不出這個基礎(chǔ)流程:
1. 選取合適的wavelet function和scaling function,從已有的信號中,反算出系數(shù)c和d。
2. 對系數(shù)做對應(yīng)處理
3. 從處理后的系數(shù)中重新構(gòu)建信號。
這里的系數(shù)處理是區(qū)別你的應(yīng)用的重點(diǎn)。比如圖像或者視頻壓縮,就希望選取能將能量聚集到很小一部分系數(shù)中的小波,然后拋棄那些能量很小的小波系數(shù),只保留少數(shù)的這些大頭系數(shù),再反變換回去。這樣的話,圖像信號的能量并沒有怎么丟失,圖像體積卻大大減小了。
還有一個沒有解釋的問題是,為什么要強(qiáng)調(diào)尺度函數(shù)和小波函數(shù)組成一個orthonormal basis呢?計算方便是一方面,還有一個原因是,如果他們滿足這個性質(zhì),就滿足瑞利能量定理,也就是說,信號的能量,可以完全用每個頻域里面的展開部分的能量,也就是他們的展開系數(shù)表示:
到這里,我們對小波變換的形式就講完了。雖然是用的最簡單的哈爾小波為例子,但舉一反三即可。我們著重介紹了多解析度分析以及它給小波變換帶來的殺手锏:時域頻域同時定位。結(jié)束之前,再多說幾句小波變換的意義。我們拿剛才例子中V3子空間的第二種可選擇的orthonormal basis作為例子:
左邊這四個basis組成元素,也就是scaling functions,的系數(shù),表征的是信號的local平均(想想它們和信號的內(nèi)積形式),而右邊的這四個basis組成元素,也就是wavelet functions,的系數(shù)則表征了在local平均中丟失的信號細(xì)節(jié)。得益于此,多解析度分析能夠?qū)π盘栐谠絹碓綄挼膮^(qū)域上取平均,等同于做低通濾波,而且,它還能保留因?yàn)槠骄鴵p失的信號細(xì)節(jié),等同于做高通濾波!這樣,我們終于可以解釋了wavelet function和scaling function背后的物理意義了:wavelet function等同于對信號做高通濾波保留變化細(xì)節(jié),而scalingfunction等同于對信號做低通濾波保留平滑的shape!
對小波變換的基礎(chǔ)知識,我們就講到這里。需要注意的是,這只是小波變換最基本最基本的知識,但也是最核心的知識。看完這里其實(shí)就是回到了最開始的介紹:小波變換是把信號分解成一系列的小波(經(jīng)過原始小波伸縮和平移得到的),這里就告訴了我們伸縮和平移
六、小波的應(yīng)用
小波是多分辨率理論的分析基礎(chǔ)。而多分辨率理論與多種分辨率下的信號表示和分析有關(guān),其優(yōu)勢很明顯--某種分辨率下無法發(fā)現(xiàn)的特性在另一個分辨率下將很容易被發(fā)現(xiàn)。從多分辨率的角度來審視小波變換,雖然解釋小波變換的方式有很多,但這種方式能簡化數(shù)學(xué)和物理的解釋過程。
對于小波的應(yīng)用很多,我學(xué)習(xí)的的方向主要是圖像處理,所以這里用圖像的應(yīng)用來舉例。對于圖像,要知道量化級數(shù)決定了圖像的分辨率,量化級數(shù)越高,圖像越是清晰,圖像的分辨率就高。
例一,哈爾小波圖像分解
例二, 小波去噪平滑
例三, 小波的邊緣檢測


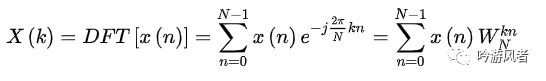
DFT、DCT和DWT之間有何聯(lián)系呢?其區(qū)別在哪?
DFT(Discrete Fourier Transform)代表著離散傅里葉變換,是作為有限長序列的在數(shù)字信號處理中被廣泛使用的一種頻域表示方法。

眾所周知,小波變換的雙正交基就來自與小波函數(shù)和尺度函數(shù),而他們通過scale和平移來得到的小波函數(shù)族和尺度函數(shù)族表示了不同小波(尺度)函數(shù)的分辨率
2023-06-27 標(biāo)簽:濾波器FPGA設(shè)計小波變換 1325 0
小波變換(wavelet transform,WT)是一種新的變換分析方法,它繼承和發(fā)展了短時傅立葉變換局部化的思想,同時又克服了窗口大小不隨頻率變化等...
2018-01-15 標(biāo)簽:小波變換 4.6萬 0

圖像小波變換原理_圖像小波變換的matlab實(shí)現(xiàn)詳解
所謂的小波的小是針對傅里葉波而言,傅里葉波指的是在時域空間無窮震蕩的正弦(或余弦波)。相對而言,小波指的是一種能量在時域非常集中的波,它的能量有限,都集...
2018-01-15 標(biāo)簽:小波變換 7.7萬 0
液晶透鏡的瞬態(tài)特性及其在擴(kuò)展景深成像中的應(yīng)用立即下載
類別:顯示及光電 2020-05-18 標(biāo)簽:小波變換成像系統(tǒng)
電流諧波畸變率怎么計算? 電流諧波畸變率是指電流中包含諧波電流的比例,它可以表示為諧波電流的有效值除以基波電流的有效值。電流諧波畸變率的計算方法取決于諧...
小波變換是如何定義的? 小波變換是一種多尺度分析方法,它可以將信號分解成不同頻率下的小波基函數(shù)。小波基函數(shù)可以表示信號的局部特征,如局部振幅和頻率,而且...
短時傅里葉變換和小波變換差別 短時傅里葉變換(short-time Fourier transform,STFT)和小波變換(wavelet trans...
小波變換與傅里葉變換的區(qū)別和聯(lián)系? 1. 傅里葉變換和小波變換的定義 傅里葉變換(Fourier Transform,簡稱FT)是一種將信號在時域上的函...

基于FPGA的快速9/7整形離散小波變換系統(tǒng)的設(shè)計過程與仿真
CCSDS圖像數(shù)據(jù)壓縮標(biāo)準(zhǔn)中采用9/7整形離散小波變換為核心算法,該算法結(jié)構(gòu)簡單,易于硬件設(shè)計實(shí)現(xiàn)。文中基于FPGA設(shè)計實(shí)現(xiàn)了9/7整數(shù)離散小波變換系統(tǒng)...
那么你可能會想到,讓窗口大小變起來,多做幾次STFT不就可以了嗎?!沒錯,小波變換就有著這樣的思路。 但事實(shí)上小波并不是這么做的(關(guān)于這一點(diǎn),方沁園同學(xué)...
基于DataSocket技術(shù)的小波消噪儀的網(wǎng)絡(luò)化
本文設(shè)計了基于Datasoket技術(shù)的虛擬小波消噪儀,實(shí)現(xiàn)了小波消噪儀的共享,硬件平臺可通過計算機(jī)與網(wǎng)絡(luò)相連,通過對虛擬儀器軟件編程實(shí)現(xiàn)儀器的的遠(yuǎn)程控制...
2011-11-03 標(biāo)簽:小波變換DataSocket消噪儀 1941 2

文中在應(yīng)用對數(shù)域電路的基礎(chǔ)上,提出了一種新型的連續(xù)小波變換方法,它通過對母小波的一種數(shù)值逼近得到小波函數(shù)的有理公式,并以Marr小波為例來模擬這個逼近過...
利用雙二次濾波器的性質(zhì), 用SI單元電路的級聯(lián)結(jié)構(gòu)來實(shí)現(xiàn)電路的靈活設(shè)計。設(shè)計舉例給出了設(shè)計思路, MATLAB仿真結(jié)果顯示這種方法的可行性。
2011-03-01 標(biāo)簽:小波變換CAD開關(guān)電流 2454 0
 換一批
換一批
編輯推薦廠商產(chǎn)品技術(shù)軟件/工具OS/語言教程專題
| 電機(jī)控制 | DSP | 氮化鎵 | 功率放大器 | ChatGPT | 自動駕駛 | TI | 瑞薩電子 |
| BLDC | PLC | 碳化硅 | 二極管 | OpenAI | 元宇宙 | 安森美 | ADI |
| 無刷電機(jī) | FOC | IGBT | 逆變器 | 文心一言 | 5G | 英飛凌 | 羅姆 |
| 直流電機(jī) | PID | MOSFET | 傳感器 | 人工智能 | 物聯(lián)網(wǎng) | NXP | 賽靈思 |
| 步進(jìn)電機(jī) | SPWM | 充電樁 | IPM | 機(jī)器視覺 | 無人機(jī) | 三菱電機(jī) | ST |
| 伺服電機(jī) | SVPWM | 光伏發(fā)電 | UPS | AR | 智能電網(wǎng) | 國民技術(shù) | Microchip |
| Arduino | BeagleBone | 樹莓派 | STM32 | MSP430 | EFM32 | ARM mbed | EDA |
| 示波器 | LPC | imx8 | PSoC | Altium Designer | Allegro | Mentor | Pads |
| OrCAD | Cadence | AutoCAD | 華秋DFM | Keil | MATLAB | MPLAB | Quartus |
| C++ | Java | Python | JavaScript | node.js | RISC-V | verilog | Tensorflow |
| Android | iOS | linux | RTOS | FreeRTOS | LiteOS | RT-THread | uCOS |
| DuerOS | Brillo | Windows11 | HarmonyOS |