這是我們Adreno?工程師Vladislav Shimanskiy 撰寫的Adreno GPU 矩陣乘法系列文章的第二部分,也是最后一個部分。上一個部分Vladislav Shimanskiy解釋了Adreno 4xx和5xx GPU系列設備端矩陣乘法(MM)內核函數和主機端參考代碼的優化實現相關概念。本文中,他將結合代碼分析,詳細介紹基于OpenCL的主機代碼和內核函數的實現。
Vlad Shimanskiy是Qualcomm? GPU計算解決方案團隊的高級工程師。
正如我上次在討論問題“GPU矩陣乘法存在哪些困難?”時提到的,由于近來依賴于卷積的深度學習引起廣泛關注,矩陣乘法(MM)運算也在GPU上變得流行起來。像Adreno GPU這樣的并行計算處理器是加速此類運算的理想選擇。然而,MM算法需要在各個計算工作項之間共享大量數據。因此,優化Adreno的MM算法需要我們利用GPU內存子系統。
在OpenCL中實現
前面已經給大家介紹了常用的四種優化技術,這里,我們進一步介紹在OpenCL中實現這些優化技術的主機參考代碼和內核函數,這些參考代碼和內核函數你將可以直接應用到你自己的代碼中。
主機代碼
首先,我們運行防止內存復制的主機代碼。如前文所述,一個矩陣通過TP/L1加載,另一個矩陣通過常規全局內存訪問路徑加載。
兩個輸入矩陣中的一個矩陣用圖像表示方法進行表示,即示例代碼中的矩陣B,通過圖像對矩陣進行抽象,并利用圖像讀取原函數訪問,如第一部分中的圖3所示。對于其他矩陣,都使用全局內存緩沖區進行存儲和訪問。這也是為什么為矩陣A和矩陣B應用不同的內存分配方式的原因。而在矩陣C的訪問和表示中,因為只需要往矩陣C是寫入數據,并且每個矩陣元素只需要寫一次,到C的流量非常低,所以矩陣C將始終通過直接路徑訪問。
矩陣A和C的內存分配
下面例程顯示了如何分配可以通過直接路徑訪問的矩陣A和C,這一點相對簡單:
cl::Buffer * buf_ptr = new cl::Buffer(*ctx_ptr, CL_MEM_READ_WRITE | CL_MEM_ALLOC_HOST_PTR, na * ma * sizeof(T));
T * host_ptr = static_cast
lda = na;
圖4通過L2緩存加載的矩陣的內存分配(A和C)
根據前面介紹,為矩陣A和C分配內存中,我們是想得到一個可以被CPU運算訪問的主機指針(CPU指針),并且希望可以通過該指針對CPU上的緩沖區進行寫入和讀取操作。因此,上述代碼的第1行中調用OpenCL的Buffer函數實現了內存分配,并得到了指向CL緩沖區的指針。
·???????? 該驅動程序分配一個緩沖區。
·???????? CL_MEM_ALLOC_HOST_PTR宏表示該內存可以被主機訪問。
·???????? 通過na和ma我們可以指定矩陣的水平和垂直維度。
注意,這里的內存不能使用malloc()函數在主機CPU上分配;必須在GPU空間中進行分配,并在CPU代碼可以寫入之前,將分配得到的內存顯式映射到具有CL API映射函數的CPU地址空間。
在調用buffer函數完成了緩沖區內存分配之后,我們必須得到host_ptr指針,在CPU上通過該指針可以訪問分配的矩陣內存。
為了得到host_ptr指針,在圖4所示代碼的第2行中,我們調用了OpenCL API中的enqueueMapBuffer,使用第1行代碼中得到的緩沖區指針buf_ptr來獲得host_ptr指針。enqueueMapBuffer函數返的host_ptr指針是一個T類型的指針(示例中T是浮點數),使用host_ptr指針可以在CPU上對分配得到的矩陣緩存區內存進行讀寫。如果我們已經分配了矩陣A,這就是我們用來傳遞該矩陣的指針。
接著我們看到圖4中代碼的第3行,這里通過lda 確定矩陣每行使用的內存量,以類型T為單位。因此,如果我們在程序中分配一個100×100矩陣,則lda將為100個T類型長度的內存空間。(注意,lda不一定等于矩陣的水平維度;在某些情況下,lda可能與之不同)。
這里,我們在主機端將lda、ldb和ldc提交給內核,以指定矩陣A、B和C的行距。
矩陣B的內存分配(圖像)
接下來我們來了解矩陣B是如何分配的,矩陣B的分配比前面介紹的矩陣A和C的分配更復雜,因為在矩陣B的分配中我們使用了2D圖像。
圖像比緩沖區限制更加嚴格。它們通常擁有4個顏色通道(RGBA),并且在內存中為圖像分配內存空間的時候必須保證適當的對齊。這里,我們先假定一個圖像,并且圖像的每個顏色分量是一個浮點數。如果我們從矩陣的角度來觀察圖像,我們希望平展顏色分量。如上所述,為提高效率,我們通過一個包括4個float類型數據的向量運算來讀取矩陣,將元素按每4個float類型打包到圖像像素中。因此,我們在計算過程中必須將矩陣的水平大小除以4,這樣我們表示的才是圖像的像素數量,具體實現代碼如下圖5所示:
cl::Image * img_ptr = new cl::Image2D(*ctx_ptr, CL_MEM_READ_WRITE | CL_MEM_ALLOC_HOST_PTR, cl::ImageFormat(CL_RGBA, CL_FLOAT), na/4, ma, 0);
cl::size_t<3> origin;
cl::size_t<3> region;
origin[0] = 0; origin[1] = 0; origin[2] = 0;
region[0] = na/4; region[1] = ma; region[2] = 1;
size_t row_pitch;
size_t slice_pitch;
T * host_ptr = static_cast
ldb = row_pitch / sizeof(T);
圖5:通過紋理管道(texture pipe) (B)加載的float32矩陣進行內存分配
上述代碼中,第1行通過調用OpenCL中的Image2D函數來分配內存,與A和C的內存分配一樣,使用了CL_MEM_ALLOC_HOST_PTR宏來指定分配的內存可以從主機端訪問。
分配得到圖像可以從主機端訪問的圖像內存后,接著看第8行,通過enqueueMapImage返回可以在CPU端使用的指針host_ptr(和前面矩陣A和C使用的enqueueMapBuffer類似),并確保我們在GPU內存中分配的圖像區域對于CPU可見。在CPU端可以通過host_ptr訪問到該圖像數據。
從CPU調用內核函數
前面已經介紹了如何分配內存,接下來介紹如何從CPU調用內核函數,該操作包括三個步驟:
?
·???????? 從CPU中取消映射,使矩陣A和B針對GPU更新。
·???????? 運行內核函數。
·???????? 重新映射,使得矩陣C中的結果對于CPU可見。
這個過程中我們還必須將A和B的內存映射回CPU,以便CPU可以更改這些矩陣;但是,這些更改不能同時被GPU和CPU獲取,需要一個同步的過程。在下面的列表中,我們利用了Snapdragon處理器上的共享虛擬內存(SVM)方法來實現內核函數運行周期和內存同步:
// update GPU mapped memory with changes made by CPU
queue_ptr->enqueueUnmapMemObject(*Abuf_ptr, (void *)Ahost_ptr);
queue_ptr->enqueueUnmapMemObject(*Bimg_ptr, (void *)Bhost_ptr);
queue_ptr->enqueueUnmapMemObject(*Cbuf_ptr, (void *)Chost_ptr);
// run kernel
err = queue_ptr->enqueueNDRangeKernel(*sgemm_kernel_ptr, cl::NullRange, global, local, NULL, &mem_event);
mem_event.wait();
// update buffer for CPU reads and following writes
queue_ptr->enqueueMapBuffer( *Cbuf_ptr, CL_TRUE, CL_MAP_READ | CL_MAP_WRITE, 0, m_aligned * n_aligned * sizeof(float));
// prepare mapped buffers for updates on CPU
queue_ptr->enqueueMapBuffer( *Abuf_ptr, CL_TRUE, CL_MAP_WRITE, 0, k_aligned * m_aligned * sizeof(float));
// prepare B image for updates on CPU
cl::size_t<3> origin;
cl::size_t<3> region;
origin[0] = 0; origin[1] = 0; origin[2] = 0;
region[0] = n_aligned/4; region[1] = k_aligned; region[2] = 1;
size_t row_pitch;
size_t slice_pitch;
queue_ptr->enqueueMapImage( *Bimg_ptr, CL_TRUE, CL_MAP_WRITE, origin, region, &row_pitch, &slice_pitch);
圖6:內核函數運行周期和內存同步過程
上述代碼實現分為兩個部分,其中第一部分是使用enqueueUnmapMemObject函數調用取消映射過程。需要傳遞對CPU端矩陣做出的所有改變,使其對于GPU可見,供乘法使用。這是一個緩存一致性事件:我們分配了矩陣A和B,在CPU端傳播,然后使它們對GPU可見,而不是復制內存。
完成了第一部分的處理,到了第二部分,GPU現在可以看到分配的矩陣了,并且可以使用。enqueueNDRangeKernel運行將對矩陣進行運算的內核函數。(經驗豐富的OpenCL程序員知道如何設置內核函數的參數,為簡潔起見,在此予以省略)。
第二部分的其余部分大同小異,不過與第一部分相反。內核函數將矩陣乘以矩陣C,因此現在我們需要使矩陣C對CPU可見。MM運算經常重復,因此我們將A和B內存映射回CPU,為下一個運算周期做好準備。在下一次迭代時,CPU能夠為A和B分配新值。
運行在GPU上的內核函數代碼
前面已經知道了如何進行內存分配和內核函數的調用,為了進一步了解整個MM運算的性能,我們來分析運行在GPU上的MM運算內核函數代碼,這部分代碼說明了擁有float 32格式元素的MM運算的本質。它是BLAS庫中SGEMM運算的簡化版本,C = αAB + βC,(為簡潔起見)其中,α= 1和β= 0。
__kernel void sgemm_mult_only(
??? ?????????????????????? __global const float *A,
??? ?????????????????????? const int lda,
??? ?????????????????????? __global float *C,
??? ?????????????????????? const int ldc,
??? ?????????????????????? const int m,
??? ?????????????????????? const int n,
??? ?????????????????????? const int k,
??? ?????????????????????? __read_only image2d_t Bi)
{
??? int gx = get_global_id(0);
??? int gy = get_global_id(1);
if (((gx << 2) < n) && ((gy << 3) < m))
??? {
??????? float4 a[8];
??????? float4 b[4];
??????? float4 c[8];
for (int i = 0; i < 8; i++)
??????? {
??????????? c[i] = 0.0f;
??????? }
int A_y_off = (gy << 3) * lda;
for (int pos = 0; pos < k; pos += 4)
??????? {
??????????? #pragma unroll
??????????? for (int i = 0; i < 4; i++)
??????????? {
??????????????? b[i] = read_imagef(Bi, (int2)(gx, pos + i));
??????????? }
int A_off = A_y_off + pos;
#pragma unroll
??????????? for (int i = 0; i < 8; i++)
??????????? {
??????????????? a[i] = vload4(0, A + A_off);
????????????? ??A_off += lda;
??????????? }
#pragma unroll
??????????? for (int i = 0; i < 8; i++)
??????????? {
??????????????? c[i] += a[i].x * b[0] + a[i].y * b[1] + a[i].z * b[2] + a[i].w * b[3];
??????????? }
}
#pragma unroll
??????? for (int i = 0; i < 8; i++)
??????? {
??????????? int C_offs = ((gy << 3) + i) * ldc + (gx << 2);
??????????? vstore4(c[i], 0, C + C_offs);
??????? }
??? }
}
?
圖7:實現C = A * B矩陣運算的內核函數示例
一般而言,我們會展開固定大小的循環,然后將從矩陣A中讀取圖像和數據的操作進行分組。具體過程如下:
·???????? 開始時,我們設置了一些限制,確保在處理矩陣時不致嚴重限制其維度,因此可以部分占用工作組。每個工作組水平和垂直地覆蓋一定數量的micro-tile,但是視乎不同的矩陣維度,我們可能面臨這樣的情況,即macro-tile中的micro-tile僅部分被矩陣占用。因此,我們要跳過macro-tile未占用部分中的任何運算;這就是這個條件的作用。矩陣維度仍然必須是4x8的倍數。
·???????? 然后,通過代碼將矩陣C的元素初始化為零。
·???????? 最外層的for循環遍歷pos參數,并包含三個子循環:
·???????? 第一個子循環中,我們通過擁有read_imagef函數的TP/L1讀取矩陣B的元素。
·???????? 第二個子循環包含直接從L2讀取的矩陣A的元素值。
·???????? 第三個子循環計算部分點積。
·???????? 注意,為提高效率,所有加載/存儲和ALU操作均使用由4個float元素構成的向量。
通過上述代碼分析,整個內核函數可能看起來比較簡單,但實際上它是一個經過高度優化、均衡的運算和數據大小組合。在使用的過程中南建議使用-cl-fast-relaxed-math標記編譯內核函數。
工作組大小
根據上述分析,macro-tile是由多個4×8 micro-tile組成。水平和垂直維度中micro-tile確切數量由2-D工作組大小確定。通常,最好使用較大的工作組,避免GPU計算單元利用不足。我們可以使用OpenCL API函數getWorkGroupInfo查詢最大工作組大小。但是,上邊界為工作組中工作項的總數。因此,我們仍然可以在總的大小的限制下,自由選擇實際的維度組成。以下是查找正確大小的一般方法:
·???????? 最小化部分占用工作組的數量。
·???????? 基于不同大小的矩陣開發啟發式算法,并在運行時使用。
·???????? 使用為特殊情況量身定制的內核函數;例如,在矩陣維度特別小的時候。
·???????? 如果GPU卸載開銷成為瓶頸,就在CPU上完成小型MM運算。
開始行動
如本文中所示,MM是一項瓶頸運算,因此,您需要在OpenCL代碼中利用上述高性能技術。這是一種加速使用Adreno GPU上內存子系統的深度學習應用的有效方法。
?
更多Qualcomm開發內容請詳見:Qualcomm開發者社區。
 電子發燒友App
電子發燒友App











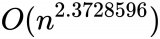
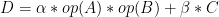










評論