圖靈 PIC嵌入式系統(tǒng)開發(fā) 551頁 126.3M 書簽版.part1共7份
2016-10-09 08:48:53
圖靈電子與電氣工程叢書——實(shí)用開關(guān)電源設(shè)計(jì)本書是一本介紹開關(guān)電源工程設(shè)計(jì)的實(shí)用指導(dǎo)書,介紹了電源實(shí)際設(shè)計(jì) 和調(diào)試工作中經(jīng)常用到的各種知識(shí),包括變換器電路拓?fù)溥x擇、元器件選擇 、儀器儀表的使用、控制
2015-01-10 01:30:32
圖靈電子與電氣工程從書-
2019-03-12 23:35:10
圖靈系列之工程師設(shè)計(jì)靈感《開關(guān)電源入門》中文版
2015-01-21 11:14:36
1、CPU=運(yùn)算器+控制器,對應(yīng)圖靈機(jī)的“讀寫頭”,但是圖靈機(jī)的讀寫頭可以自動(dòng)取紙帶上數(shù)據(jù)、做運(yùn)算、存結(jié)果。而馮氏結(jié)構(gòu)中進(jìn)行改進(jìn),就是讀程序、翻譯程序、執(zhí)行程序。其中讀程序和執(zhí)行程序?qū)?yīng)于“自動(dòng)
2021-12-20 08:18:48
想用LABVIEW寫一個(gè)程序鏈接到圖靈機(jī)器人,需要通過網(wǎng)頁傳遞數(shù)據(jù),LABVIEW要怎么弄啊,越簡單越好~
2016-04-22 20:27:09
整數(shù)字世界的誕生。 03數(shù)字世界的問題求解方式雖然我們將第一臺(tái)計(jì)算機(jī)ENIAC稱之為“計(jì)算機(jī)”,一臺(tái)能夠像人一樣進(jìn)行科學(xué)計(jì)算的機(jī)器,事實(shí)也確實(shí)是如此。但別忘了ENIAC是基于“圖靈機(jī)”這一理論模型,而圖靈機(jī)
2020-07-06 08:34:53
、蘋果等一個(gè)又一個(gè)行業(yè)巨頭。從圖靈機(jī)到物聯(lián)網(wǎng),歷史的鏡頭緊隨著科技飛速發(fā)展的步伐。物聯(lián)網(wǎng)提供了機(jī)器設(shè)備間相互溝通的渠道,越來越多的設(shè)備都被賦予了“智能硬件”的稱號(hào)。伴隨著智能硬件的興起,機(jī)器離人工智能已經(jīng)
2015-08-05 10:26:17
。2、圖靈以及百度API創(chuàng)建語音項(xiàng)目并修改配置文件測試程序內(nèi)置的API為項(xiàng)目主人個(gè)人申請的免費(fèi)版本,直接用還是不好的,而且可能人用的多會(huì)有一定的影響,因此,筆者自己從圖靈機(jī)器人云端以及百度API云端
2017-10-12 23:25:08
。一般來說,大公司不考慮這些,但咱們只是玩玩,就沒必要花錢買板子了,所以另選了圖靈(百度搜索圖靈機(jī)器人)即可。圖靈跟微信的結(jié)合效果是什么呢?我想給朋友試試調(diào)戲機(jī)器人的感覺,所以關(guān)閉了過濾,然后所有人都懵逼了
2016-11-13 12:55:58
,接著將文字發(fā)送到圖靈機(jī)器人服務(wù)器,返回應(yīng)答語句,再把應(yīng)答語句傳向服務(wù)器轉(zhuǎn)化為語音,由聲音播放模塊輸出。本人榮獲廣東省第四屆合泰杯單片機(jī)應(yīng)用設(shè)計(jì)邀請賽二等獎(jiǎng),中國機(jī)器人大賽武術(shù)擂臺(tái)賽二等獎(jiǎng)。想要嘗試用香橙派做人工智能開發(fā)。
2016-12-08 16:08:35
狀態(tài),當(dāng)麥克風(fēng)采集到人聲時(shí),開啟對話模式。語音輸入系統(tǒng)后,由系統(tǒng)向服務(wù)器解析為文字,接著將文字發(fā)送到圖靈機(jī)器人服務(wù)器,返回應(yīng)答語句,再把應(yīng)答語句傳向服務(wù)器轉(zhuǎn)化為語音,由聲音播放模塊輸出。作品實(shí)現(xiàn)了
2017-02-25 21:26:18
`圖靈經(jīng)典嵌入式學(xué)習(xí)書籍`
2021-03-31 11:00:18
水平的提高上,也有很少一部分的公司專注于機(jī)器人大腦的開發(fā),比如圖靈機(jī)器人團(tuán)隊(duì),他們就致力于人機(jī)交互層面的軟件技術(shù)研發(fā),植入圖靈機(jī)器人大腦之后的機(jī)器人擁有的智商可以和一個(gè)七到八歲孩子匹敵。據(jù)了解,圖靈機(jī)
2015-09-16 15:40:27
的噪聲包括光照、遮擋、傾斜、文字堆疊、文字鑲嵌、透視變化等等,這對于OCR算法的適應(yīng)能力更具挑戰(zhàn)性。為攻克這些難題,阿里安全圖靈實(shí)驗(yàn)室的研究人員設(shè)計(jì)了基于深度學(xué)習(xí)的網(wǎng)絡(luò)模型和算法。據(jù)介紹,圖靈實(shí)驗(yàn)室
2018-03-14 10:54:50
,讓無數(shù)人對家用服務(wù)機(jī)器人充滿期待。事實(shí)上,家用“大白”正在慢慢走進(jìn)人們的現(xiàn)實(shí)生活。 據(jù)了解,當(dāng)前能讓“大白”走進(jìn)現(xiàn)實(shí)的技術(shù)服務(wù)包括圖靈機(jī)器人團(tuán)隊(duì)在內(nèi),這個(gè)號(hào)稱全球中文語境下智能度最高的機(jī)器人大腦,可以
2015-08-10 18:16:12
文章目錄圖靈機(jī)編碼EncodingASCII編碼從晶體管到概念CPU通用CPU微控制器MCUARM Cortex-M指令集圖靈機(jī)可計(jì)算性(calculability)是指一個(gè)實(shí)際問題是否可以使用計(jì)
2021-12-14 08:39:12
”的RNN在圖像識(shí)別中的成功運(yùn)用 )4、神經(jīng)圖靈機(jī)依然有趣,但還無法勝任實(shí)際工作當(dāng)你翻譯一句話時(shí),并不會(huì)逐個(gè)詞匯進(jìn)行,而是會(huì)從句子的整體結(jié)構(gòu)出發(fā)。機(jī)器難以做到這一點(diǎn),這一挑戰(zhàn)被稱為“強(qiáng)耦合輸出的整體
2015-12-23 14:21:58
來進(jìn)行數(shù)據(jù)存取,用戶在關(guān)注微信公眾號(hào)后可查詢所關(guān)注地點(diǎn)的溫濕度情況。同時(shí)該系統(tǒng)將微信公眾平臺(tái)與圖靈機(jī)器人結(jié)合,在聯(lián)網(wǎng)的環(huán)境下可做到和人自如的對話。本系統(tǒng)具有成本低,安裝維護(hù)方便,用戶操作簡便等特點(diǎn)
2017-02-22 19:46:45
描述光線追蹤性能),每秒 500T OPs 深度學(xué)習(xí),支持 NVLink,每秒 100GB,支持每秒 500 萬億張量的操作。黃仁勛表示,圖靈架構(gòu)是自 2006 年 CUDA GPU 發(fā)明以來最大的飛躍
2018-08-15 10:59:45
電子發(fā)燒友網(wǎng)站提供《圖靈電子與電氣工程叢書PLC教程 第3版.txt》資料免費(fèi)下載
2014-09-03 08:27:18 0
0 [圖靈電子與電氣工程叢書].FPGA設(shè)計(jì)實(shí)戰(zhàn)
2016-05-04 11:09:51 12
12 圖靈 電子電氣工程師必知必會(huì)!分2部分上傳,需要的朋友可以下載!!!!
2016-11-05 16:14:38 0
0 圖靈 電子電氣工程師必知必會(huì)!分2部分上傳,需要的朋友可以下載!!!!
2016-11-05 16:14:38 0
0 圖靈樣本V4.0-小
2016-12-25 22:29:29 0
0 一則關(guān)于“試愛機(jī)器人”的視頻風(fēng)靡網(wǎng)絡(luò),這一機(jī)器人是由圖靈機(jī)器人和百合網(wǎng)共同推出的,意在幫助缺乏經(jīng)驗(yàn)、自信的單身人群,練習(xí)戀愛溝通技能。盡管如此,還是有些人想到了“人機(jī)戀”這樣的熱門話題,也有的人把她與“性愛機(jī)器人”掛鉤。
2016-12-23 13:31:11 1215
1215 圖靈與人工智能 談到人工智能,我們就不得 不提起計(jì)算機(jī)先驅(qū)圖靈。艾 倫麥席森圖靈(Alan Mathison Turing,19121954),英國數(shù)學(xué) 家、邏輯學(xué)家,被稱為計(jì)算機(jī)之 父、人工智能
2017-09-13 20:16:52 4
4 11月10日,圖靈機(jī)器人開放平臺(tái)知識(shí)庫模塊開放內(nèi)測,這是繼開放聊天對話接口之后,圖靈機(jī)器人平臺(tái)對外輸出的又一核心能力。包含了圖靈機(jī)器人多個(gè)身份屬性接口、完整的知識(shí)庫管理接口以及機(jī)器人批量生成接口
2017-09-20 12:56:36 0
0 計(jì)算機(jī)先驅(qū)者以圖靈機(jī)為模型制造了第一代計(jì)算機(jī),其中比較知名的是美國軍方的ENIAC計(jì)算機(jī),這個(gè)計(jì)算機(jī)幾乎完全克隆了圖靈機(jī)的設(shè)計(jì),ENIAC程序是在多組插板上的跳線,形成了類似于圖靈機(jī)的狀態(tài)遷移
2017-10-10 15:57:02 6
6 自動(dòng)機(jī)是計(jì)算機(jī)的簡單理論模型,通常將自動(dòng)機(jī)分為有限自動(dòng)機(jī)和圖靈機(jī)。盡管有限自動(dòng)機(jī)更簡單,但在定義圖靈機(jī)之后數(shù)年,這個(gè)概念才被提出來。
2017-10-13 06:52:00 9306
9306 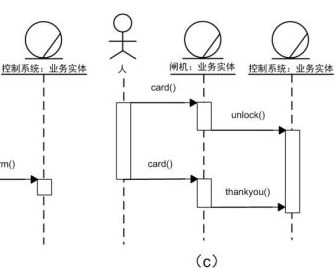
圖靈測試由艾倫·麥席森·圖靈發(fā)明,指測試者與被測試者(一個(gè)人和一臺(tái)機(jī)器)隔開的情況下,通過一些裝置(如鍵盤)向被測試者隨意提問。進(jìn)行多次測試后,如果有超過30%的測試者不能確定出被測試者是人還是機(jī)器,那么這臺(tái)機(jī)器就通過了測試,并被認(rèn)為具有人類智能。
2017-12-28 15:19:53 8871
8871 如果艾倫·圖靈還活著,今年他該過百歲生日了。只可惜,這個(gè)計(jì)算機(jī)科學(xué)和人工智能之父的生命之鐘,在極富創(chuàng)造力的黃金年齡段就停擺了。人工智能之父圖靈之死:謎一樣的解謎者。
2018-01-03 11:51:02 24061
24061 所謂的圖靈機(jī)就是指一個(gè)抽象的機(jī)器,它有一條無限長的紙帶,紙帶分成了一個(gè)一個(gè)的小方格,每個(gè)方格有不同的顏色。有一個(gè)機(jī)器頭在紙帶上移來移去。機(jī)器頭有一組內(nèi)部狀態(tài),還有一些固定的程序。在每個(gè)時(shí)刻,機(jī)器
2018-01-03 13:55:21 70201
70201 圖靈機(jī)的模型介紹雖然有些無趣,不過請堅(jiān)持看下去,我會(huì)在下面運(yùn)用大家比較好理解的形式重新解釋的。在這里你僅僅需要認(rèn)識(shí)它的輪廓。
2018-01-03 14:18:36 47980
47980 圖靈測試指測試者與被測試者(一個(gè)人和一臺(tái)機(jī)器)隔開的情況下,通過一些裝置(如鍵盤)向被測試者隨意提問。
2018-01-03 15:03:50 19556
19556 圖靈提出了一種測試機(jī)器是不是具備人類智能的方法。即假設(shè)有一臺(tái)電腦,其運(yùn)算速度非常快、記憶容量和邏輯單元的數(shù)目也超過了人腦,而且還為這臺(tái)電腦編寫了許多智能化的程序,并提供了合適種類的大量數(shù)據(jù),那么,是否就能說這臺(tái)機(jī)器具有思維能力?
2018-05-01 10:45:00 34566
34566 
日前,有著“計(jì)算機(jī)界的諾貝爾獎(jiǎng)”之稱的“圖靈獎(jiǎng)”揭開面紗。國際計(jì)算機(jī)協(xié)會(huì)宣布,美國科學(xué)家約翰·軒尼詩和大衛(wèi)·帕特森獲得2017年度圖靈獎(jiǎng),以表彰二人開創(chuàng)了一種系統(tǒng)的、可量化的方法用以設(shè)計(jì)和評(píng)價(jià)計(jì)算機(jī)體系架構(gòu),并對精簡指令集(RISC)微處理器行業(yè)產(chǎn)生深遠(yuǎn)影響。
2018-04-02 10:05:28 6963
6963 是1930年代在調(diào)查函數(shù)定義、函數(shù)應(yīng)用和遞歸時(shí)研發(fā)的一個(gè)形式系統(tǒng),是等價(jià)于圖靈機(jī)的一種抽象的計(jì)算模型,許多函數(shù)式編程語言都可看成是在?演算基礎(chǔ)上精心制作出的結(jié)果
2018-04-03 11:01:40 3
3 圖靈機(jī)器人有三個(gè)基本功能: (1)語音識(shí)別:將語音識(shí)別成相應(yīng)的文本。 (2)語義理解:將文本識(shí)別成領(lǐng)域相關(guān)的語義結(jié)果。 (3)語音合成 : 將文本轉(zhuǎn)化成語音讀出。 要集成圖靈機(jī)器人,首先要進(jìn)行圖靈
2018-04-13 09:49:27 9212
9212 
在香港亞洲博覽館2號(hào)館,鎂客網(wǎng)和環(huán)球資源聯(lián)合主辦了一場以“A Big Dive Into AI , Big Data And Machine Learning”為主題的研討會(huì), 圖靈機(jī)
2018-04-15 09:55:00 12900
12900 基于itchat庫開發(fā)的網(wǎng)頁版微信機(jī)器人類庫,具體的使用方法可以打開下面的鏈接學(xué)習(xí)(對itchat熟悉的朋友也可以直接引用itchat類),在這里還用到了一個(gè)圖靈機(jī)器人,他已經(jīng)封裝到了wxpy庫中,這樣可以讓微信機(jī)器人除了拍照和攝像,還能進(jìn)行簡單的問答聊天。
2018-04-26 16:36:50 10151
10151 作為當(dāng)前人工智能主流的“機(jī)器學(xué)習(xí)”與圖靈所探討的“學(xué)習(xí)機(jī)器”,其思考的角度和深刻性完全不同,啟迪良多。
2018-06-13 09:39:03 4845
4845 根據(jù)有限狀態(tài)控制器的當(dāng)前狀態(tài)及每個(gè)讀寫頭讀到的帶符號(hào),圖靈機(jī)的一個(gè)計(jì)算步可實(shí)現(xiàn)下面3個(gè)操作之一或全部。
2018-06-22 16:12:07 1764
1764 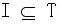
近日,在加拿大溫哥華舉行的 SIGGRAPH會(huì)上,NVIDIA(英偉達(dá))公司創(chuàng)始人黃仁勛發(fā)布了全新的圖靈 (Turing) 繪圖架構(gòu)。
2018-08-15 15:57:57 3957
3957 量子計(jì)算是一種遵循量子力學(xué)規(guī)律調(diào)控量子信息單元進(jìn)行計(jì)算的新型計(jì)算模式。對照于傳統(tǒng)的通用計(jì)算機(jī),其理論模型是通用圖靈機(jī);通用的量子計(jì)算機(jī),其理論模型是用量子力學(xué)規(guī)律重新詮釋的通用圖靈機(jī)。
2018-11-04 10:23:14 26505
26505 作者:(美國)丹尼爾·希利斯。《通靈芯片(計(jì)算機(jī)運(yùn)作的簡單原理)》深入淺出地闡述了計(jì)算機(jī)科學(xué)中許多基本而重要的概念,包括布爾邏輯、有限自動(dòng)機(jī)、編程語言、圖靈機(jī)的普遍性、信息論、算法、并行計(jì)算、量子
2018-12-04 08:00:00 10
10 幾十年來,這個(gè)問題的常見答案一直是通過“圖靈測試”。這個(gè)測試以著名數(shù)學(xué)家艾倫·圖靈(Alan Turing)的名字命名。圖靈說,如果一臺(tái)機(jī)器能夠通過文本界面與人類進(jìn)行對話,使人類無法區(qū)分人類和機(jī)器,那么這臺(tái)機(jī)器就是智能的。
2019-01-07 09:48:23 3547
3547 在這方面,有很多值得借鑒的例子,例如Google DeepMind科學(xué)家2014年為建立“神經(jīng)圖靈機(jī)”所做的努力。 該項(xiàng)目使用所謂的“循環(huán)神經(jīng)網(wǎng)絡(luò)”來發(fā)現(xiàn)簡單的計(jì)算機(jī)算法,例如復(fù)制和粘貼文本。
2019-01-21 08:43:35 3200
3200 在Kadena我們經(jīng)常談?wù)搮^(qū)塊鏈設(shè)計(jì)決策。我最近遇到的一個(gè)特別深刻的設(shè)計(jì)決策是關(guān)于圖靈完備的,它在我們的一個(gè)開發(fā)人員最近的一篇文章中引發(fā)了爭論。作為團(tuán)隊(duì)的非技術(shù)成員,我想了解圖靈完備的真正含義,為什么區(qū)塊鏈社區(qū)在這個(gè)問題上存在分歧,為什么我們的工程師在努力教育其他人安全智能合約編程的缺點(diǎn)。
2019-02-15 14:06:42 896
896 當(dāng)?shù)貢r(shí)間3月27日,新一屆“圖靈獎(jiǎng)”正式出爐,該獎(jiǎng)項(xiàng)被授予深度學(xué)習(xí)領(lǐng)域的三名研究科學(xué)家,他們分別是:蒙特利大學(xué)的教授Yoshua Bengio,Google工程師和哥倫多大學(xué)Geoffrey Hintion,F(xiàn)acebook的首席人工智能科學(xué)家和紐約大學(xué)教授Yann LeCun。
2019-03-29 14:05:22 6040
6040 阿蘭?圖靈在1937年首次提出了一個(gè)通用計(jì)算設(shè)備的設(shè)想。他設(shè)想所有的計(jì)算都可能在一種特殊的機(jī)器上執(zhí)行,這就是現(xiàn)在所說的圖靈機(jī)。如果我們把計(jì)算機(jī)定義成一個(gè)數(shù)據(jù)處理器,計(jì)算機(jī)就可以被看作是一個(gè)接收輸入
2019-05-09 18:16:00 0
0 python關(guān)于開發(fā)微信的庫主要有itchat和wxpy,而wxpy底層是調(diào)用的itchat,所以如果你只是要使用的話建議使用wxpy庫,它比其他的庫都要優(yōu)雅,更面向?qū)ο螅疑疃日狭?b class="flag-6" style="color: red">圖靈機(jī)器人和小i機(jī)器人。
2019-04-28 11:16:42 3228
3228 
說到圖靈完備一般得先提到圖靈機(jī)的概念,圖靈機(jī)是英國數(shù)學(xué)家阿蘭·麥席森·圖靈在1963年提出的、為了研究可計(jì)算問題而構(gòu)思的抽象計(jì)算模型——將人們傳統(tǒng)的使用紙筆進(jìn)行數(shù)學(xué)運(yùn)算的過程,進(jìn)行抽象,由一個(gè)虛擬的機(jī)器替代人們進(jìn)行無數(shù)次的數(shù)學(xué)運(yùn)算。這個(gè)虛擬的機(jī)器就是圖靈機(jī),也就是現(xiàn)在計(jì)算機(jī)的雛形。
2019-04-28 11:49:33 6037
6037 如果從阿蘭·圖靈1943年首次提出“圖靈機(jī)”的概念算起,AI已經(jīng)經(jīng)歷了86年的發(fā)展史。本文以信息圖的形式回顧了這70多年的標(biāo)志性事件,并歸納出AI發(fā)展的幾個(gè)方向和技術(shù)應(yīng)用,以及10大AI企業(yè)和國家排行榜。
2019-05-08 11:07:18 4573
4573 如果從阿蘭·圖靈1943年首次提出“圖靈機(jī)”的概念算起,AI已經(jīng)經(jīng)歷了86年的發(fā)展史。本文以信息圖的形式回顧了這70多年的標(biāo)志性事件,并歸納出AI發(fā)展的幾個(gè)方向和技術(shù)應(yīng)用,以及10大AI企業(yè)和國家排行榜。
2019-05-11 10:16:39 2769
2769 計(jì)算機(jī)的先哲圖靈在設(shè)計(jì)圖靈機(jī)的同時(shí)也一直在思考怎么讓機(jī)器更智能,可以說計(jì)算芯片從誕生的那一刻起就是為智能服務(wù)的。
2019-06-07 13:45:00 490
490 圖靈獎(jiǎng)得主:如何利用AI和機(jī)器學(xué)習(xí)應(yīng)對氣候變化,當(dāng)?shù)貢r(shí)間6月5日,新晉圖靈獎(jiǎng)得主、深度學(xué)習(xí)領(lǐng)域的開拓性人物Yoshua Bengio(約書亞本吉奧)在他的“主場”加拿大蒙特利爾米其林開拓前行峰會(huì)上演講,他分享的主題是“人工智能和機(jī)器學(xué)習(xí)技術(shù)如何幫助應(yīng)對氣候變化”。
2019-07-01 10:28:30 503
503 我認(rèn)為圖靈機(jī)制在誕生在很早的生命階段,現(xiàn)在的圖靈機(jī)制是大腦皮層高度擴(kuò)大之后,提供的擴(kuò)展能力呈現(xiàn)出來的,至少我認(rèn)為從有眼睛開始注意機(jī)制就應(yīng)該存在了,只是那個(gè)時(shí)候更多是一種反射機(jī)制,舊腦連接,新腦是爬行類之后才開始出現(xiàn)的。
2019-07-06 09:08:00 9528
9528 
預(yù)言機(jī)(oracle machine),又稱諭示機(jī),是一種抽象電腦,用來研究決定型問題。可以被視為一個(gè)多了個(gè)黑盒子(預(yù)言者)的圖靈機(jī),這個(gè)黑盒子的功能是可以在單一運(yùn)算之內(nèi)解答特定問題。這樣看來,區(qū)塊鏈領(lǐng)域的預(yù)言機(jī)也是像一個(gè)黑盒子,用來解決區(qū)塊鏈與現(xiàn)實(shí)世界中間的特定數(shù)據(jù)問題。
2019-07-11 10:47:08 854
854 8月15日,未來圖靈&大眾網(wǎng)簽約儀式在北京舉行,由財(cái)視傳媒打造的圖靈指數(shù)AI明星企業(yè)排行榜正式對外發(fā)布。
2019-08-16 14:48:19 2321
2321 第一代數(shù)字化思維的代表是圖靈,他創(chuàng)造了圖靈機(jī),圖靈機(jī)的特點(diǎn)是“程序是程序,數(shù)據(jù)是數(shù)據(jù)”。
2019-11-01 10:53:50 1151
1151 2007年圖靈獎(jiǎng)得主愛德蒙·克拉克(Edmund M. Clarke)因感染新冠肺炎于當(dāng)?shù)貢r(shí)間12月22日不幸去世。
2020-12-24 15:56:19 2445
2445 由于代碼重用攻擊的方式方法多樣,相應(yīng)的 gadget在結(jié)構(gòu)上也不盡相同,目前尚沒有一種通用的方法能夠用來描述多種代碼重用攻擊下的 gadget。結(jié)合幾種常見代碼重用攻擊的攻擊模型和圖靈機(jī)模型,文中
2021-05-29 16:29:30 5
5 圖靈程序設(shè)計(jì)叢書《Python編程:從入門到實(shí)踐》
2021-12-30 14:49:12 0
0 歷經(jīng)5年的沉淀,松靈機(jī)器人著重打造專屬『通用型移動(dòng)底盤機(jī)器人』標(biāo)簽,以獨(dú)特設(shè)計(jì)風(fēng)格,標(biāo)準(zhǔn)化平臺(tái)的產(chǎn)品理念。讓松靈機(jī)器人產(chǎn)品在國內(nèi)外收獲好評(píng),實(shí)現(xiàn)移動(dòng)底盤機(jī)器人銷量位居全國首位,并很快在海外
2022-05-10 15:03:31 2471
2471 
最近ChatGPT很火啊,我也去試著玩了一下。
當(dāng)然我一上來就想給它做一個(gè)圖靈測試的改進(jìn)版。
為什么不是做圖靈測試呢?
因?yàn)?b class="flag-6" style="color: red">圖靈測試存在很多已知的問題,并且不能代表
2023-02-14 09:41:13 0
0 為基礎(chǔ),二次開發(fā)植入百度AI開放平臺(tái)的語音技術(shù)、圖靈機(jī)器人的中文環(huán)境對話技術(shù)和機(jī)智云技術(shù),以達(dá)到使用微信客戶端文本或語音輸入控制與管理設(shè)備的效果,解決了家電設(shè)備之間的互聯(lián)互控
2022-04-28 15:41:36 372
372 
人工智能技術(shù)的發(fā)展歷程可以追溯到數(shù)百年前。18世紀(jì)初期,一些數(shù)學(xué)家已經(jīng)開始探索如何用機(jī)器模擬人的思維過程從而實(shí)現(xiàn)人工智能。不過,直到20世紀(jì)40年代,圖靈提出了通用圖靈機(jī)的概念,才真正將計(jì)算理論和人工智能領(lǐng)域聯(lián)系起來。
2023-08-14 15:03:10 1122
1122 隨著技術(shù)的不斷發(fā)展,焊接工藝也得到了顯著的改進(jìn)和創(chuàng)新。在焊接領(lǐng)域,一項(xiàng)關(guān)鍵技術(shù)是焊縫跟蹤,它對焊接的質(zhì)量和效率至關(guān)重要。創(chuàng)想焊縫跟蹤傳感器是一項(xiàng)革命性的技術(shù),它結(jié)合了機(jī)器視覺和自動(dòng)化控制,為焊接過程帶來了前所未有的精度和可靠性。 創(chuàng)想焊縫跟蹤傳感器 創(chuàng)想焊縫跟蹤傳感器是一種先進(jìn)的設(shè)備,旨在監(jiān)測焊接過程中的焊縫位置,實(shí)現(xiàn)自動(dòng)化焊接過程的精確控制。它采用機(jī)器視覺技術(shù),通過相機(jī)和圖像處理軟件,能夠在實(shí)時(shí)監(jiān)測
2023-10-13 16:26:49 200
200 
全球領(lǐng)先的智能機(jī)器人獨(dú)角獸企業(yè)思靈機(jī)器人宣布完成對機(jī)器人公司Franka Emika收購。
2023-11-03 18:27:48 915
915 圖靈機(jī)是圖靈提出的一種抽象的計(jì)算模型,被認(rèn)為是計(jì)算機(jī)科學(xué)的基礎(chǔ)。在圖靈機(jī)模型中,包含了以下幾個(gè)組成部分:輸入帶、讀寫頭、狀態(tài)集合、轉(zhuǎn)移函數(shù)以及輸出。 首先,輸入帶是圖靈機(jī)的數(shù)據(jù)存儲(chǔ)器,可以看作是一條
2023-12-20 17:23:01 999
999 據(jù)寶信軟件《2023年半年度報(bào)告》顯示,2023年上半年,寶信軟件全面提升高端自動(dòng)化業(yè)務(wù)能力,“軟硬兼施”,持續(xù)加大機(jī)器人、PLC、工藝模型等領(lǐng)域投入,解決“卡脖子”問題,助力產(chǎn)業(yè)智慧升級(jí),確保關(guān)鍵核心技術(shù)自主可控。
2023-12-26 17:35:34 569
569 聯(lián)想入股中科慧靈機(jī)器人公司 日前聯(lián)想入股中科慧靈機(jī)器人公司,北京中科慧靈機(jī)器人技術(shù)有限公司成立于2023年8月,是一家面向智能機(jī)器人、人工智能服務(wù)的企業(yè),聯(lián)想的入股或是在加大對智能機(jī)器人的布局。
2024-03-21 16:46:34 267
267
 電子發(fā)燒友App
電子發(fā)燒友App

















































評(píng)論