圖靈機(jī)的組成：

1.一條無(wú)限長(zhǎng)的紙帶 TAPE。紙帶被劃分為一個(gè)接一個(gè)的小格子，每個(gè)格子上包含一個(gè)來自有限字母表的符號(hào)，字母表中有一個(gè)特殊的符號(hào) 表示空白。紙帶上的格子從左到右依此被編號(hào)為 0，1，2，。.. ，紙帶的右端可以無(wú)限伸展。

2.一個(gè)讀寫頭 HEAD。該讀寫頭可以在紙帶上左右移動(dòng)，它能讀出當(dāng)前所指的格子上的符號(hào)，并能改變當(dāng)前格子上的符號(hào)。

3.一套控制規(guī)則 TABLE。它根據(jù)當(dāng)前機(jī)器所處的狀態(tài)以及當(dāng)前讀寫頭所指的格子上的符號(hào)來確定讀寫頭下一步的動(dòng)作，并改變狀態(tài)寄存器的值，令機(jī)器進(jìn)入一個(gè)新的狀態(tài)。

4.一個(gè)狀態(tài)寄存器。它用來保存圖靈機(jī)當(dāng)前所處的狀態(tài)。圖靈機(jī)的所有可能狀態(tài)的數(shù)目是有限的，并且有一個(gè)特殊的狀態(tài)，稱為停機(jī)狀態(tài)。參見停機(jī)問題。

關(guān)于圖靈機(jī)的模型介紹

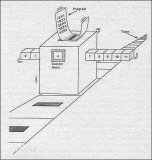
圖靈機(jī)的模型介紹雖然有些無(wú)趣，不過請(qǐng)堅(jiān)持看下去，我會(huì)在下面運(yùn)用大家比較好理解的形式重新解釋的。在這里你僅僅需要認(rèn)識(shí)它的輪廓。一個(gè)圖靈機(jī)是形如下面的一個(gè)裝置：

這個(gè)裝置由下面幾個(gè)部分組成：一個(gè)無(wú)限長(zhǎng)的紙帶，一個(gè)讀寫頭。（中間那個(gè)大盒子），內(nèi)部狀態(tài)（盒子上的方塊，比如A，B，E，H ），另外，還有一個(gè)程序?qū)@個(gè)盒子進(jìn)行控制。這個(gè)裝置就是根據(jù)程序的命令以及它的內(nèi)部狀態(tài)進(jìn)行磁帶的讀寫、移動(dòng)。它工作的時(shí)候是這樣的：從讀寫頭在紙帶上讀出一個(gè)方格的信息，并且根據(jù)它當(dāng)前的內(nèi)部狀態(tài)開始對(duì)程序進(jìn)行查表，然后得出一個(gè)輸出動(dòng)作，也就是是否往紙帶上寫信息，還是移動(dòng)讀寫頭到下一個(gè)方格。程序也會(huì)告訴它下一時(shí)刻內(nèi)部狀態(tài)轉(zhuǎn)移到哪一個(gè)。

具體的程序就是一個(gè)列表，也叫做規(guī)則表，是這樣的：

當(dāng)前內(nèi)部狀態(tài)s 輸入數(shù)值i 輸出動(dòng)作o 下一時(shí)刻的內(nèi)部狀態(tài)s‘

B 1 前移C

A 0 往紙帶上寫1 B

C 0 后移A

… … … …

因此，圖靈機(jī)只要根據(jù)每一時(shí)刻讀寫頭讀到的信息和當(dāng)前的內(nèi)部狀態(tài)進(jìn)行查表就可以確定它下一時(shí)刻的內(nèi)部狀態(tài)和輸出動(dòng)作了。

圖靈機(jī)就是這么簡(jiǎn)單！不可思議吧？而只要你變化它的程序（也就是上面的規(guī)則表），那么它就可能為你做任何計(jì)算機(jī)能夠完成的工作。因此可以說，圖靈機(jī)就是一個(gè)最簡(jiǎn)單的計(jì)算機(jī)模型！

也許，你會(huì)覺得圖靈機(jī)模型太簡(jiǎn)單，怎么可能完成計(jì)算機(jī)的復(fù)雜任務(wù)呢？問題的關(guān)鍵是如何理解這個(gè)模型。
#e#

如何理解圖靈機(jī)？

1、小蟲的比喻

我們不妨考慮這樣一個(gè)問題。假設(shè)一個(gè)小蟲在地上爬，那么我們應(yīng)該怎樣從小蟲信息處理的角度來建立它的模型？

首先，我們需要對(duì)小蟲所在的環(huán)境進(jìn)行建模。我們不妨就假設(shè)小蟲所處的世界是一個(gè)無(wú)限長(zhǎng)的紙帶，這個(gè)紙帶上被分成了若干小的方格，而每個(gè)方格都僅僅只有黑和白兩種顏色。很顯然，這個(gè)小蟲要有眼睛或者鼻子或者耳朵等等感覺器官來獲得世界的信息，我們不妨把模型簡(jiǎn)化，假設(shè)它僅僅具有一個(gè)感覺器官：眼睛，而且它的視力短得可憐，也就是說它僅僅能夠感受到它所處的方格的顏色。因而這個(gè)方格所在的位置的黑色或者白色的信息就是小蟲的輸入信息。

另外，我們當(dāng)然還需要為小蟲建立輸出裝置，也就是說它能夠動(dòng)起來。我們?nèi)匀豢紤]最簡(jiǎn)單的情況：小蟲的輸出動(dòng)作就是往紙帶上前爬一個(gè)方格或者后退一個(gè)方格。

僅僅有了輸入裝置以及輸出裝置，小蟲還不能動(dòng)起來，原因很簡(jiǎn)單，它并不知道該怎樣在各種情況下選擇它的輸出動(dòng)作。于是我們就需要給它指定行動(dòng)的規(guī)則，這就是程序！假設(shè)我們記小蟲的輸入信息集合為I={黑色，白色}，它的輸出可能行動(dòng)的集合就是：O={前移，后移}，那么程序就是要告訴它在給定了輸入比如黑***況下，它應(yīng)該選擇什么輸出。因而，一個(gè)程序就是一個(gè)從I 集合到O 集合的映射。我們也可以用列表的方式來表示程序，比如： 程序1：

輸入輸出

黑色前移

白色后移

這個(gè)程序非常簡(jiǎn)單，它告訴小蟲當(dāng)讀到一個(gè)黑色方格的時(shí)候就往前走一個(gè)方格，當(dāng)讀到一個(gè)白色方格的時(shí)候就后退一個(gè)格。

我們不妨假設(shè)，小蟲所處的世界的一個(gè)片斷是：黑黑黑白白黑白……，小蟲從左端開始。 那么小蟲讀到這個(gè)片斷會(huì)怎樣行動(dòng)呢？它先讀到黑色，然后根據(jù)程序前移一個(gè)方格，于是就會(huì)得到另外一個(gè)黑色信息，這個(gè)時(shí)候它會(huì)根據(jù)程序再次前移一個(gè)方格，仍然是黑色，再前移，這個(gè)時(shí)候就讀到白色方格了，根據(jù)程序它應(yīng)該后退一個(gè)格，這個(gè)時(shí)候輸入就是黑色了，前移，白色，后移……，可以預(yù)見小蟲會(huì)無(wú)限的循環(huán)下去。

然而，現(xiàn)實(shí)世界中的小蟲肯定不會(huì)這樣傻的在那里無(wú)限循環(huán)下去。我們還需要改進(jìn)這個(gè)最簡(jiǎn)

單的模型。首先，我們知道小蟲除了可以機(jī)械地在世界上移動(dòng)以外，還會(huì)對(duì)世界本身造 ……

開始

成影響，因而改變這個(gè)世界。比如蟲子看到旁邊有食物，它就會(huì)把那個(gè)東西吃掉了。在我們這個(gè)模型中，也就相當(dāng)于我們必須假設(shè)小蟲可以改寫紙帶上的信息。因而，小蟲可能的輸出動(dòng)作集合就變成了：O={前移，后移，涂黑，涂白}。這個(gè)時(shí)候，我們可以把程序1改為比如： 程序2：

輸入輸出

黑前移

白涂黑

紙帶是黑黑白白黑……，小蟲會(huì)怎樣行動(dòng)呢？下面的圖表示出了這個(gè)例子中每一步小蟲的位置（標(biāo)有圓點(diǎn)的方格就是小蟲的當(dāng)前位置），以及紙帶的狀況。

開始：小蟲在最左邊的方格，根據(jù)程序的第一行，讀入黑色應(yīng)該前移。

第二步：仍然讀入黑，根據(jù)程序的第一行，前移。

第三步：這個(gè)時(shí)候讀入的是白色，根據(jù)程序的第二行，應(yīng)該把這個(gè)方格涂黑，而沒有其他的動(dòng)作。假設(shè)這張圖上方格仍然沒有涂黑，而在下一時(shí)刻才把它表示出來。

第四步：當(dāng)前方格已經(jīng)是黑色的，因此小蟲讀入黑色方格，前移。

第五步：讀入白色，涂黑方格，原地不動(dòng)。

第六步：當(dāng)前的方格已經(jīng)被涂黑，繼續(xù)前移。

第七步：讀入黑色，前移

小蟲的動(dòng)作還會(huì)持續(xù)下去……。我們看到，小蟲將會(huì)不停的重復(fù)上面的動(dòng)作不斷往前走，并會(huì)把所有的紙帶涂黑。

顯然，你還可以設(shè)計(jì)出其他的程序來，然而無(wú)論你的程序怎么復(fù)雜，也無(wú)論紙帶子的情況如何，小蟲的行為都會(huì)要么停留在一個(gè)方格上，要么朝一個(gè)方向永遠(yuǎn)運(yùn)動(dòng)下去，或者就是在幾個(gè)方格上來回打轉(zhuǎn)。然而，無(wú)論怎樣，小蟲比起真實(shí)世界中的蟲子來說，還有一個(gè)致命的弱點(diǎn)：那就是如果你給它固定的輸入信息，它都會(huì)給你固定的輸出信息！因?yàn)槲覀冎莱绦蚴枪趟赖模虼耍慨?dāng)黑色信息輸入的時(shí)候，無(wú)論如何它都僅僅前移一個(gè)方格，而不會(huì)做出其他的反應(yīng)。它似乎真的是機(jī)械的！

如果我們進(jìn)一步更改小蟲模型，那么它就會(huì)有所改進(jìn)，至少在給定相同輸入的情況下，小蟲會(huì)有不同的輸出情況。這就是加入小蟲的內(nèi)部狀態(tài)！我們可以作這樣的一個(gè)比喻：假設(shè)黑色方格是食物，蟲子可以吃掉它，而當(dāng)吃到一個(gè)食物后，小蟲子就會(huì)感覺到飽了。當(dāng)讀入的信息是白色方格的時(shí)候，雖然沒有食物但它仍然吃飽了，只有當(dāng)再次讀入黑色時(shí)候它才會(huì)感覺到自己饑餓了。因而，我們說小蟲具有兩個(gè)內(nèi)部狀態(tài)，并把它內(nèi)部狀態(tài)的集合記為：S={饑餓，吃飽}。這樣小蟲行為的時(shí)候就會(huì)不僅根據(jù)它的輸入信息，而且也會(huì)根據(jù)它當(dāng)前的內(nèi)部狀態(tài)來決定它的輸出動(dòng)作，并且還要更改它的內(nèi)部狀態(tài)。而它的這一行動(dòng)仍然要用程序控制，只不過跟上面的程序比起來，現(xiàn)在的程序就更復(fù)雜一些了，比如：

程序3：

輸入當(dāng)前內(nèi)部狀態(tài)輸出下時(shí)刻的內(nèi)部狀態(tài)

黑饑餓涂白吃飽

黑吃飽后移饑餓

白饑餓涂黑饑餓

白吃飽前移吃飽

這個(gè)程序復(fù)雜多了，有四行，原因是你不僅需要指定每一種輸入情況下小蟲應(yīng)該采取的動(dòng)作，而且還要指定在每種輸入和內(nèi)部狀態(tài)的組合情況下小蟲應(yīng)該怎樣行動(dòng)。看看我們的蟲子在讀入黑白白黑白……這樣的紙帶的時(shí)候，會(huì)怎樣？仍然用下面的一系列圖來表示，灰色的圓點(diǎn)表示饑餓的小蟲，白色的圓點(diǎn)表示它吃飽了。為了清晰，我們把小蟲將要變成的狀態(tài)寫到了圖的下一行。

假定它仍然從左端開始，而且開始的時(shí)候小蟲處于饑餓狀態(tài)。這樣讀入黑色，當(dāng)前饑餓狀態(tài)，根據(jù)程序第一行，把方格涂白，并變成吃飽（這相當(dāng)于把那個(gè)食物吃了，注意吃完后，小蟲并沒動(dòng)）。

第二步：當(dāng)前的方格變成了白色，因而讀入白色，而當(dāng)前的狀態(tài)是吃飽狀態(tài)，那么根據(jù)程序中的第四條前移，仍然是吃飽狀態(tài)；

第三步：讀入白色，當(dāng)前狀態(tài)是吃飽，因而會(huì)重復(fù)第二步的動(dòng)作。

涂白方格，變成吃飽

前移，仍然吃飽

前移，保持吃飽

第四步：仍然重復(fù)上次的動(dòng)作。

第五步：讀入黑色，當(dāng)前狀態(tài)是吃飽，這時(shí)候根據(jù)程序的第二行應(yīng)該后移方格，并轉(zhuǎn)入饑餓狀態(tài)；

第六步：讀入白色，當(dāng)前饑餓狀態(tài)，根據(jù)程序第三行應(yīng)該涂黑，并保持饑餓狀態(tài)（各位注意，這位小蟲似乎自己吐出了食物！）；

第七步，讀入黑色，當(dāng)前饑餓，于是把方格涂白，并轉(zhuǎn)入吃飽狀態(tài)（呵呵，小蟲把剛剛自己吐出來的東西又吃掉了！）。

第八步，讀入白色，當(dāng)前吃飽，于是前移，保持吃保狀態(tài)。

這時(shí)候跟第四步的情況完全一樣了，因而小蟲會(huì)完全重復(fù)5、6、7、8步的動(dòng)作，并永遠(yuǎn)循環(huán)下去。似乎最后的黑色方格是一個(gè)門檻，小蟲無(wú)論如何也跨越不過去了。

小蟲的行為比以前的程序復(fù)雜了一些。盡管從長(zhǎng)期來看，它最后仍然會(huì)落入機(jī)械的循環(huán)或者無(wú)休止的重復(fù)。然而這從本質(zhì)上已經(jīng)與前面的程序完全不同了，因?yàn)楫?dāng)你輸入給小蟲白色信息的時(shí)候，它的反應(yīng)是你不能預(yù)測(cè)的！它有可能涂黑方格也有可能前移一個(gè)。當(dāng)然前提是你不能打開小蟲看到它的內(nèi)部結(jié)構(gòu)，也不能知道它的程序，那么你所看到的就是一個(gè)不能預(yù)測(cè)的滿地亂爬的小蟲。如果小蟲的內(nèi)部狀態(tài)數(shù)再增多呢，那么它的行為會(huì)更加的不可預(yù)測(cè)！ 好了，如果你已經(jīng)徹底搞懂了我們的小蟲是怎么工作的，那么你已經(jīng)明白了圖靈機(jī)的工作原理了！因?yàn)閺谋举|(zhì)上講，最后的小蟲模型就是一個(gè)圖靈機(jī)！
#e#

2、如何理解圖靈機(jī)模型

剛才用小蟲說明了圖靈機(jī)的工作原理，相信你的第一個(gè)反映就是，這樣的模型太簡(jiǎn)單了！他根本說明不了現(xiàn)實(shí)世界中的任何問題！下面，我就要試圖說服你，圖靈機(jī)這個(gè)模型是偉大的！ 首先，我想說的是，其實(shí)我們每一個(gè)會(huì)決策、會(huì)思考的人就可以被抽象的看成一個(gè)圖靈機(jī)。 前移，保持吃飽

涂白，轉(zhuǎn)入吃飽

前移，保持吃飽

后移，變成饑餓

涂黑，保持饑餓

為什么可以做這種抽象呢？首先我們可以考慮擴(kuò)展剛才說的小蟲模型。因?yàn)樾∠x模型是以一切都簡(jiǎn)化的前提開始的，所以它的確是太太簡(jiǎn)單了。然而，我們可以把小蟲的輸入集合、輸出行動(dòng)集合、內(nèi)部狀態(tài)集合進(jìn)行擴(kuò)大，這個(gè)模型就一下子實(shí)用多了。首先，小蟲完全可以處于一個(gè)三維的空間中而不是簡(jiǎn)簡(jiǎn)單單的紙帶。并且小蟲的視力很好，它一下子能讀到方圓500米的信息，當(dāng)然，小蟲也可以擁有其他的感覺器官，比如嗅覺、聽覺等等，而這些改變都僅僅是擴(kuò)大了輸入集合的維數(shù)和范圍，并沒有其他更本質(zhì)的改變。同樣道理，小蟲可能的輸出集合也是異常的豐富，它不僅僅能移動(dòng)自己，還可以盡情的改造它所在的自然界。進(jìn)一步的，小蟲的內(nèi)部狀態(tài)可能非常的多，而且控制它行為的程序可能異常復(fù)雜，那么小蟲會(huì)有什么本事呢？這就很難說了，因?yàn)殡S著小蟲內(nèi)部的狀態(tài)數(shù)的增加，隨著它所處環(huán)境的復(fù)雜度的增加，我們正在逐漸失去對(duì)小蟲行為的預(yù)測(cè)能力。但是所有這些改變?nèi)匀粵]有逃出圖靈機(jī)的模型：輸入集合、輸出集合、內(nèi)部狀態(tài)、固定的程序！就是這四樣?xùn)|西抓住了小蟲信息處理的根本。

我們?nèi)四懿荒芤脖贿@樣的抽象呢？顯然，輸入狀態(tài)集合就是你所處的環(huán)境中能夠看到、聽到、聞到、感覺到的所有一起，可能的輸出集合就是你的每一言每一行，以及你能夠表達(dá)出來的所有表情動(dòng)作。內(nèi)部狀態(tài)集合則要復(fù)雜得多。因?yàn)槲覀兛梢园讶我庖粋€(gè)神經(jīng)細(xì)胞的狀態(tài)組合看作是一個(gè)內(nèi)部狀態(tài)，那么所有可能的神經(jīng)細(xì)胞的狀態(tài)組合將是天文數(shù)字！

似乎你會(huì)說，這個(gè)模型根本不對(duì)，還有很多思維本質(zhì)的東西沒有概括進(jìn)去。比如記憶問題，人有記憶，圖靈機(jī)有么？其實(shí)，只要圖靈機(jī)具有了內(nèi)部狀態(tài)，它就相應(yīng)的具有了記憶。比如上面講到的具有饑餓和吃飽兩種狀態(tài)的小蟲就會(huì)記住它所經(jīng)歷過的世界：如果吃到食物就用吃飽狀態(tài)來“記住”吃過的食物。什么是記憶呢？假如你經(jīng)歷了一件事情并記住了它，那么只要你下一次的行動(dòng)在相同條件下和你記住這件事情之前的行動(dòng)不一樣了，就說明該事情對(duì)你造成了影響，也就說明你確實(shí)記住了它。

學(xué)習(xí)的問題反映在模型中了么？學(xué)習(xí)是怎么回事兒呢？似乎圖靈機(jī)模型中不包括學(xué)習(xí)，因?yàn)閷W(xué)習(xí)就意味著對(duì)程序的改變，而圖靈機(jī)是不能在運(yùn)行過程中改變它的程序的。然而，我們不難假設(shè)，你實(shí)際上并不能打開一個(gè)人的腦袋來看，所以它的實(shí)際程序規(guī)則你是不知道的。很有可能一個(gè)圖靈機(jī)的規(guī)則沒有改變，只不過激活了它的某些內(nèi)部狀態(tài)，因而它的行為發(fā)生了本質(zhì)上的變化，盡管給它相同的輸入，它給出了完全不同的輸出，因而在我們看來，它似乎會(huì)學(xué)習(xí)了！而實(shí)際上，這個(gè)圖靈機(jī)的程序一點(diǎn)都沒變。

還有很多很多現(xiàn)象似乎都能被圖靈機(jī)包括，什么是人類的情緒、情感？你完全可以把它看作是某種內(nèi)部狀態(tài)，因而處于心情好的情緒下，你的輸入輸出是一套規(guī)則，而心情不好的時(shí)候則完全是另一套。這仍然沒有逃出圖靈機(jī)的模型范圍。

接下來的問題就是我們?nèi)说乃季S究竟是不是和圖靈機(jī)一樣遵循固定的程序呢？這個(gè)問題似乎初看是不可能的，因?yàn)槿说男袨樘还潭耍∧悴豢深A(yù)言它！然而我會(huì)爭(zhēng)辯道，無(wú)論如何神經(jīng)元傳遞信息、變化狀態(tài)的規(guī)律都是固定的，可以被程序化的，那么作為神經(jīng)元的整體：腦的運(yùn)作必然也要遵循固定的規(guī)則也就是程序了。那么，如果是這樣，正如圖靈相信的，

人腦也不會(huì)超越圖靈機(jī)這個(gè)模型，所以，人工智能也必然是可能的！然而，我認(rèn)為針對(duì)這個(gè)問題的答案很有可能沒有這么簡(jiǎn)單，我們將在最后詳細(xì)討論這個(gè)問題。

無(wú)論如何，我相信你已經(jīng)能夠體會(huì)到了，圖靈機(jī)模型實(shí)際上是非常強(qiáng)有力的！

計(jì)算與圖靈機(jī)

1、什么是計(jì)算

說了這么多，雖然也許你已經(jīng)了解到了圖靈機(jī)的威力，也許還將信將疑，然而，你肯定仍然看不出來圖靈機(jī)和計(jì)算有什么關(guān)系。而實(shí)際上，圖靈機(jī)是一個(gè)理論計(jì)算機(jī)模型，它最主

要的能耐還是在于計(jì)算上！所以，下面我們就來看看什么是計(jì)算！

我可以先給出一個(gè)很摩登的對(duì)計(jì)算概念的理解：廣義上講，一個(gè)函數(shù)變化如把x 變成了f（x）就是一個(gè)計(jì)算！如果我們把一切都看作是信息，那么更精確的講，計(jì)算就是對(duì)信息的變換！如果采用這種觀點(diǎn)，你會(huì)發(fā)現(xiàn)，其實(shí)自然界充滿了計(jì)算！如果我們把一個(gè)小球扔到地上，小球又彈起來了，那么大地就完成了一次對(duì)小球的計(jì)算。因?yàn)槟阃耆梢园研∏虻倪\(yùn)動(dòng)都抽象成信息，它無(wú)非是一些比如位置、速度、形狀等等能用信息描述的東西嘛，而大地把小球彈起來就無(wú)非是對(duì)小球的這些信息進(jìn)行了某種變換，因而大地就完成了一次計(jì)算！你可以把整個(gè)大地看作是一個(gè)系統(tǒng)，而扔下去的小球是對(duì)這個(gè)系統(tǒng)的輸入，那么彈回來的小球就是該系統(tǒng)的輸出，因而也可以說，計(jì)算就是某個(gè)系統(tǒng)完成了一次從輸入到輸出的變換！

這樣理解不要緊，你會(huì)發(fā)現(xiàn)，現(xiàn)實(shí)世界到處都是計(jì)算了！因?yàn)槲覀兺耆梢园阉械淖匀唤绱嬖诘倪^程都抽象成這樣的輸入輸出系統(tǒng)，所有的大自然存在的變量都看作是信息，因而計(jì)算無(wú)處不在！也的確，正是采取了這樣的觀點(diǎn)，國(guó)外才有可能發(fā)明什么DNA 計(jì)算機(jī)、生物計(jì)算機(jī)、量子計(jì)算機(jī)這些新鮮玩藝！因?yàn)槿思野袲NA 的化學(xué)反應(yīng)、量子世界的波函數(shù)變換都看作是計(jì)算了，自然就會(huì)人為地把這些計(jì)算組合起來構(gòu)成計(jì)算機(jī)了。然而，似乎我們的理論家們還在力圖證明關(guān)于圖靈機(jī)的某個(gè)定理呢，卻完全沒有意識(shí)到計(jì)算其實(shí)就是這樣簡(jiǎn)單！

下面回到圖靈機(jī)！為什么說圖靈機(jī)是一個(gè)計(jì)算的裝置呢？很簡(jiǎn)單，圖靈機(jī)也是一個(gè)會(huì)對(duì)輸入信息進(jìn)行變換給出輸出信息的系統(tǒng)。比如前面說的小蟲，紙帶上的一個(gè)方格一個(gè)方格的顏色信息就是對(duì)小蟲的輸入，而小蟲所采取的行動(dòng)就是它的輸出。不過這么看，你會(huì)發(fā)現(xiàn)，似乎小蟲的輸出太簡(jiǎn)單了。因?yàn)樗鼉H僅就有那么幾種簡(jiǎn)單的輸出動(dòng)作。然而，不要忘了，復(fù)雜性來源于組合！雖然每一次小蟲的輸出動(dòng)作很簡(jiǎn)單，然而當(dāng)把所有這些輸出動(dòng)作組合在一起，就有可能非常復(fù)雜！比如我們可以把初始時(shí)刻的紙帶看作是輸入信息，那么經(jīng)過任意長(zhǎng)的時(shí)間比如說100年后，小蟲通過不斷的涂抹紙帶最后留下的信息就是輸出信息了。那么小蟲完成的過程就是一次計(jì)算。事實(shí)上，在圖靈機(jī)的正規(guī)定義中，存在一個(gè)所謂的停機(jī)狀態(tài)，當(dāng)圖靈機(jī)一到停機(jī)狀態(tài)，我們就認(rèn)為它計(jì)算完畢了，因而不用費(fèi)勁的等上100年。

2、計(jì)算的組合

更有意思的是，我們可以把若干個(gè)計(jì)算系統(tǒng)進(jìn)行合并構(gòu)成更大的計(jì)算系統(tǒng)。比如還是那個(gè)小球吧，如果往地上放了一個(gè)蹺蹺板，這樣小球掉到地上會(huì)彈起這個(gè)蹺蹺板的另一端，而蹺蹺板的另一邊可能還是一個(gè)小球，于是這個(gè)彈起的小球又會(huì)砸向另一個(gè)蹺蹺板……。

我們自然可以通過組合若干圖靈機(jī)完成更大更多的計(jì)算，如果把一個(gè)圖靈機(jī)對(duì)紙帶信息變換的結(jié)果又輸入給另一臺(tái)圖靈機(jī)，然后再輸入給別的圖靈機(jī)……，這就是把計(jì)算進(jìn)行了組合！也許你還在為前面說的無(wú)限多的內(nèi)部狀態(tài)，無(wú)限復(fù)雜的程序而苦惱，那么到現(xiàn)在，你不難明白，實(shí)際上我們并不需要寫出無(wú)限復(fù)雜的程序列表，而僅僅將這些圖靈機(jī)組合到一起就可以產(chǎn)生復(fù)雜的行為了。

有了圖靈機(jī)的組合，我們就能夠從最簡(jiǎn)單的圖靈機(jī)開始構(gòu)造復(fù)雜的圖靈機(jī)。那么最簡(jiǎn)單的圖靈機(jī)是什么呢？我們知道最簡(jiǎn)單的信息就是0和1，而最簡(jiǎn)單的計(jì)算就是對(duì)0或1進(jìn)行布爾運(yùn)算。而布爾運(yùn)算本質(zhì)上其實(shí)就三種：與、或、非。從最簡(jiǎn)單的邏輯運(yùn)算操作最簡(jiǎn)單的

二進(jìn)制信息出發(fā)我們其實(shí)可以構(gòu)造任意的圖靈機(jī)！這點(diǎn)不難理解：任何圖靈機(jī)都可以把輸入、輸出信息進(jìn)行01的編碼，而任何一個(gè)變換也可以最終分解為對(duì)01編碼的變換，而對(duì)01編碼的所有計(jì)算都可分解成前面說的三種運(yùn)算。也許，現(xiàn)在你明白了為什么研究計(jì)算機(jī)的人都要去研究基本的布爾電路。奧秘就在于，用布爾電路可以組合出任意的圖靈機(jī)！

3、征服無(wú)限的方法

回憶你小時(shí)候是如何學(xué)會(huì)加法運(yùn)算的。剛開始的時(shí)候，你僅僅會(huì)死記硬背。比如你記住了1+1=2，記住了2+4=6，……。然而無(wú)論你記住多少固定數(shù)字的運(yùn)算，你都不叫學(xué)會(huì)了加法。原因很簡(jiǎn)單，假如你記住了n 對(duì)數(shù)的加法，那么我總會(huì)拿出第n+1對(duì)數(shù)是你沒有記住的，因此你還是不會(huì)計(jì)算。原則上。自然數(shù)的個(gè)數(shù)是無(wú)窮的，所以任何兩個(gè)數(shù)的加法可能結(jié)果也是無(wú)窮的，而如果采用死記硬背的方法，我們頭腦怎么可能記住無(wú)窮數(shù)字的計(jì)算法則呢？但是隨著年齡的增長(zhǎng)，你畢竟還是最終學(xué)會(huì)了加法運(yùn)算！說來奇怪，你肯定明白其實(shí)加法運(yùn)算并不需要記住所有數(shù)字的運(yùn)算結(jié)果，而僅僅需要記住10以內(nèi)的任意兩個(gè)數(shù)的和，并且懂得了進(jìn)位法則就可以了。

你是怎么做到的呢？假設(shè)要計(jì)算32+69的加法結(jié)果，你會(huì)把32寫到一行，把69寫到下一行，然后把他們對(duì)齊。于是你開始計(jì)算2+9=11，進(jìn)一位，然后計(jì)算3+6=9，再計(jì)算9+1=10再進(jìn)一位，最后，再把計(jì)算的這些每一位的結(jié)果都拼起來就是最終的答案101。這個(gè)簡(jiǎn)單例子給我們的啟發(fā)就是：作加法的過程就是一個(gè)機(jī)械的計(jì)算過程，這里輸入就是32和69這兩個(gè)數(shù)字，輸出就是101。而你的程序規(guī)則就是具體的把任意兩個(gè)10以內(nèi)的數(shù)求和。這樣，根據(jù)固定的加法運(yùn)算程序你可以計(jì)算任兩個(gè)數(shù)的加法了。

不知你發(fā)現(xiàn)了沒有，這個(gè)計(jì)算加法的方法能夠讓你找到運(yùn)用有限的規(guī)則應(yīng)對(duì)無(wú)限可能情況的方法！我們剛才說了，實(shí)際上自然數(shù)是無(wú)限的，這樣，所有可能的加法結(jié)果也是無(wú)限的。然而運(yùn)用剛才說的運(yùn)算方法，無(wú)論輸入的數(shù)字是多少，只要你把要計(jì)算的數(shù)字寫下來了，就一定能夠計(jì)算出最終的結(jié)果，而無(wú)需死記硬背所有的加法！

因而，可以說計(jì)算這個(gè)簡(jiǎn)單的概念，是一種用有限來應(yīng)對(duì)無(wú)限的方法！我們?cè)倏匆粋€(gè)例子：假如給你一組數(shù)對(duì)：1，2 3，6 5，10 18，36，就這4對(duì)，這時(shí)問你102對(duì)應(yīng)的數(shù)是多少？很顯然，如果僅僅根據(jù)你掌握的已知數(shù)對(duì)的知識(shí)，是不可能知道答案的，因?yàn)槟愕闹R(shí)庫(kù)里面沒有存放著102對(duì)應(yīng)數(shù)字的知識(shí)。然而，如果你掌握了產(chǎn)生這組數(shù)對(duì)的程序法則，也就是看到如果第一個(gè)數(shù)是x ，那么第二個(gè)數(shù)就是2x 的話，你肯定一下子就算出102對(duì)應(yīng)的是204了。也就是說，你實(shí)際上運(yùn)用2x 這兩個(gè)字符就記住了無(wú)限的諸如1，2 3，6 102，204所有這樣的數(shù)對(duì)。

這看起來似乎很奇怪。我怎么可能運(yùn)用有限的字符來應(yīng)對(duì)無(wú)限種可能呢？實(shí)際上，當(dāng)沒有人問你問題的時(shí)候，你存儲(chǔ)的2x 什么也沒有，而當(dāng)我問你102對(duì)應(yīng)的是多少？我就相當(dāng)于給你輸入了信息：102，而你僅僅是根據(jù)這個(gè)輸入信息102進(jìn)行一系列的加工變換得到了輸出信息204。因而輸入信息就好比是原材料，而你的程序規(guī)則就是加工的方法，只有在原材料上進(jìn)行加工，你才能輸出最終產(chǎn)品。

這讓我不禁想起了專家系統(tǒng)方法。其實(shí)專家系統(tǒng)就是一個(gè)大的規(guī)則庫(kù)。也就相當(dāng)于存儲(chǔ)了很多很多的1，2 3，6 5，10這樣特殊的規(guī)則對(duì)。而無(wú)論它存儲(chǔ)的東西再多，總歸會(huì)是有限的，你只要找到一個(gè)它沒有存儲(chǔ)到的問題，它就無(wú)能為力了。因而專家系統(tǒng)就會(huì)在你問到102對(duì)應(yīng)是多少的時(shí)候失敗！如何解決問題？人們想出了很多方法，就比如元規(guī)則的方法，其實(shí)元規(guī)則就相當(dāng)于剛才所說的計(jì)算加法的程序，或者2x 這樣的東西。運(yùn)用元規(guī)則的確可以應(yīng)對(duì)無(wú)限種情況了。所以，這就是為什么你問計(jì)算機(jī)任何兩個(gè)數(shù)相加是多少，它總能給出你正確的答案的原因，雖然它不必記住所有這些加法對(duì)的信息。

然而僅僅是元規(guī)則就能解決所有問題么？

假如給你三組數(shù)對(duì)，排列成一個(gè)表：

1，2 3，6 4，8 100，200

3，9 2，6 8，24 100，300

1，4 2，8 3，12 100，400

那么問你在第6行上，3這個(gè)數(shù)字對(duì)應(yīng)的是多少？我們先要找出第一行的規(guī)律是2x 沒有疑問，第二行呢？是3x ，第三行是4x ，那么第6行就應(yīng)該是7x 了，因而在第6行上3

應(yīng)該對(duì)應(yīng)的是21了！這里跟前面不太一樣的是，雖然我們得到了每一行的規(guī)則比如第一行的2x ，但是隨著行數(shù)的增加，這個(gè)規(guī)則本身也變化了，因而第2行是3x ，第3行是4x 等等，因而我們又得到了一個(gè)規(guī)則本身的規(guī)則，即如果行數(shù)是n 的話，那么這一行的規(guī)則就是（n+1）x。我們顯然能夠根據(jù)輸入的n 和x 計(jì)算出數(shù)值。把這個(gè)道理放到專家系統(tǒng)里面，這種原理就是元規(guī)則的規(guī)則，元規(guī)則的元規(guī)則……，應(yīng)該是無(wú)窮的！然而專家系統(tǒng)本身并不會(huì)自動(dòng)的歸納這些規(guī)則，人必須事先把這些元規(guī)則寫到程序里，這也就是專家系統(tǒng)最大的弊端。而我們?nèi)怂坪蹩偰茉谝恍﹤€(gè)別的事件中歸納出規(guī)則。進(jìn)一步問，機(jī)器可以歸納么？這就相當(dāng)于說：可以為歸納方法編出程序么？這也是一個(gè)很有趣的問題，下面將要詳細(xì)討論！可以設(shè)想，假如我們找到了真正歸納的方法，那么編寫出這樣的程序，它就會(huì)一勞永逸的自己進(jìn)行學(xué)習(xí)歸納了。我們完全再也不用給他編制程序和規(guī)則了。這正是人工智能的終極目標(biāo)！