研究人員在研究圖像處理算法時提出了CNN(卷積神經網絡)的概念。傳統的全連接網絡是一種黑盒子 - 它接收所有輸入并通過每個值傳遞到一個dense 網絡,然后再傳遞給一個熱輸出。這似乎適用于少量的輸入。
當我們處理1024x768像素的圖像時,我們輸入3x1024x768 = 2359296個數字(每個像素的RGB值)。使用2359296個數字的輸入向量的dense多層神經網絡在第一層中每個神經元至少具有2359296個權重 - 第一層的每個神經元具有2MB的權重。對于處理器以及RAM,在20世紀90年代和2000年除,這幾乎是不可能的。
這導致研究人員想知道是否有更好的方法來完成這項工作。任何圖像處理(識別)中的第一個也是最重要的任務通常是檢測邊緣和紋理。接下來是識別和處理真實對象。很明顯要注意檢測紋理和邊緣實際上并不依賴于整個圖像。人們需要查看給定像素周圍的像素以識別邊緣或紋理。
此外,用于識別邊緣或紋理的算法在整個圖像中應該是相同的。我們不能對圖像的中心或任何角落或側面使用不同的算法。檢測邊緣或紋理的概念必須相同。我們不需要為圖像的每個像素學習一組新參數。
這種理解導致了卷積神經網絡。網絡的第一層由掃描圖像的小塊神經元組成 - 一次處理幾個像素。通常這些是9或16或25像素的正方形。
CNN非常有效地減少了計算量。小的“filter/kernel”沿著圖像滑動,一次處理一小塊。整個圖像所需的處理非常相似,因此非常有效。
雖然它是為圖像處理而引入的,但多年來,CNN已經在許多其他領域中得到應用。
一個例子
?
現在我們已經了解了CNN的基本概念,讓我們了解數字的工作原理。正如我們所看到的,邊緣檢測是任何圖像處理問題的主要任務。讓我們看看CNN如何用于解決邊緣檢測問題。 ?
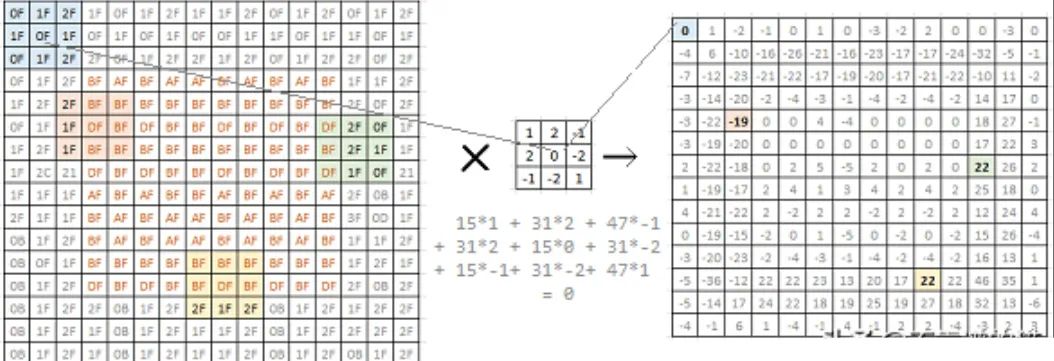
? ? 左邊是16x16單色圖像的位圖。矩陣中的每個值表示相應像素的亮度。我們可以看到,這是一個簡單的灰色圖像,中間有一個方塊。當我們嘗試將其用2x2 filter(中圖)進行卷積時,我們得到一個14x14的矩陣(右圖)。 ?
我們選擇的filter 可以突出顯示圖像中的邊緣。我們可以在右邊的矩陣中看到,原始圖像中與邊緣對應的值是高的(正的或負的)。這是一個簡單的邊緣檢測filter。研究人員已經確定了許多不同的filter,可以識別和突出圖像的各個不同方面。在典型的卷積神經網絡(CNN)模型開發中,我們讓網絡自己學習和發現這些filters。
?
重要概念
?
以下是我們在進一步使用CNN之前應該了解的一些重要概念。
Padding
卷積filter的一個明顯問題是每一步都通過減小矩陣大小來減少“信息” - 縮小輸出。基本上,如果原始矩陣是N×N,并且filter是F×F,則得到的矩陣將是(N-F + 1)×(N-F + 1)。這是因為邊緣上的像素比圖像中間的像素少。
如果我們在所有邊上按(F - 1)/ 2像素填充圖像,則將保留N×N的大小。
因此,我們有兩種類型的卷積,即Valid Convolution和 Same Convolution。Valid 實質上意味著沒有填充。因此每個卷積都會導致尺寸減小。Same Convolution使用填充,以便保留矩陣的大小。
在計算機視覺中,F通常是奇數。奇數F有助于保持圖像的對稱性,也允許一個中心像素,這有助于在各種算法中應用均勻偏差。因此,3x3, 5x5, 7x7 filter是很常見的。我們還有1x1個filter。
Strided
我們上面討論的卷積是連續的,因為它連續掃描像素。我們也可以使用strides - 通過在圖像上移動卷積filter時跳過s像素。
因此,如果我們有nxn圖像和fxf filter并且我們用stride s和padding p進行卷積,則輸出的大小為:((n + 2p -f)/ s + 1)x((n + 2p -f)/ s + 1)
卷積v / s互相關
互相關基本上是在底部對角線上翻轉矩陣的卷積。翻轉會將關聯性添加到操作中。但在圖像處理中,我們不會翻轉它。
RGB圖像上的卷積
現在我們有一個nxnx 3圖像,我們用fxfx 3 filter進行卷積。因此,我們在任何圖像及其filter中都有高度,寬度和通道數。任何時候,圖像中的通道數量與filter中的通道數量相同。這個卷積的輸出有寬度和高度(n-f + 1)和1通道。
多個filters
一個3通道圖像與一個3通道filter卷積得到一個單一通道輸出。但我們并不局限于一個filter。我們可以有多個filters——每個filter都會產生一個新的輸出層。因此,輸入中的通道數應該與每個filter中的通道數相同。filters的數量和輸出通道的數量是一樣的。
因此,我們從3個通道的圖像開始,并在輸出中以多個通道結束。這些輸出通道中的每一個都表示圖像的某些特定方面,這些方面由相應的filter拾取。因此,它也被稱為特征而不是通道。在一個真正的深層網絡中,我們還添加了一個偏差和一個非線性激活函數,如RelU。
池化層
池化基本上是將值組合成一個值。我們可以有平均池,最大池化,最小化池等。因此,使用fxf池化的nxn輸入將生成(n/f)x(n/f)輸出。它沒有需要學習的參數。 ?
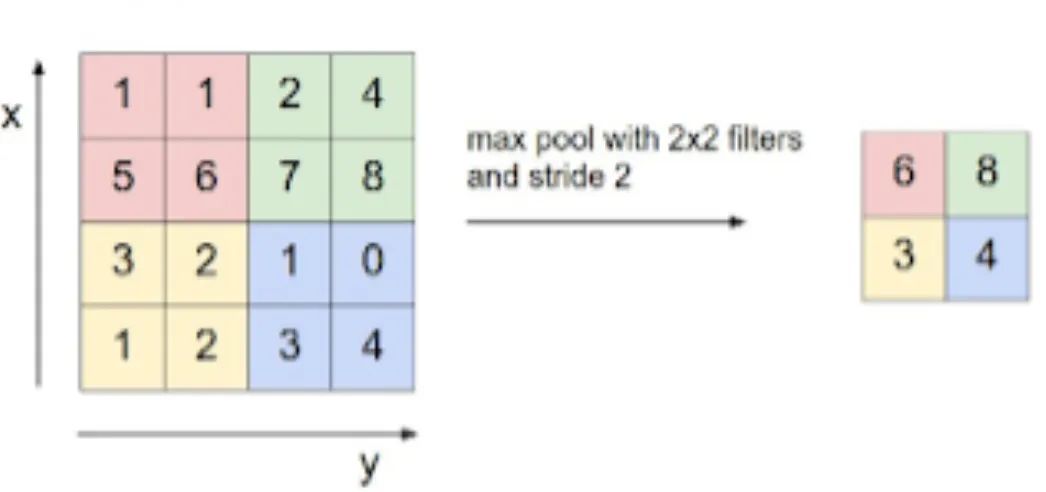
最大池化
CNN架構
典型的中小型CNN模型遵循一些基本原則。

? 典型的CNN架構
交替卷積和池化層
逐漸減小frame 大小并增加frame 數,
朝向末端的Flat 和全連接層
對所有隱藏層激活RelU,然后為最終層激活softmax
隨著我們轉向大型和超大型網絡,事情變得越來越復雜。研究人員為我們提供了更多可以在這里使用的具體架構(如:ImageNet, GoogleNet和VGGNet等)。
?
Python實現
?
通常實現CNN模型時,先進行數據分析和清理,然后選擇我們可以開始的網絡模型。我們根據網絡數量和層大小及其連接性的布局提供架構 - 然后我們允許網絡自己學習其余部分。然后我們可以調整超參數來生成一個足以滿足我們目的的模型。
讓我們看一個卷積網絡如何工作的簡單例子。
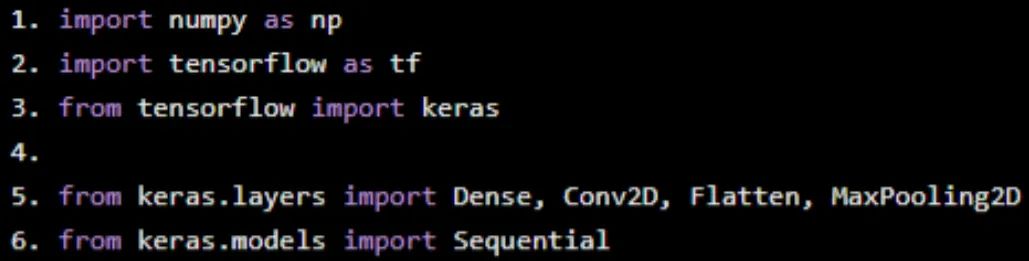
導入模塊
我們首先導入所需的Python庫。
import numpy as np import tensorflow as tf from tensorflow import keras from keras.layers import Dense, Conv2D, Flatten, MaxPooling2D from keras.models import Sequential
?
?
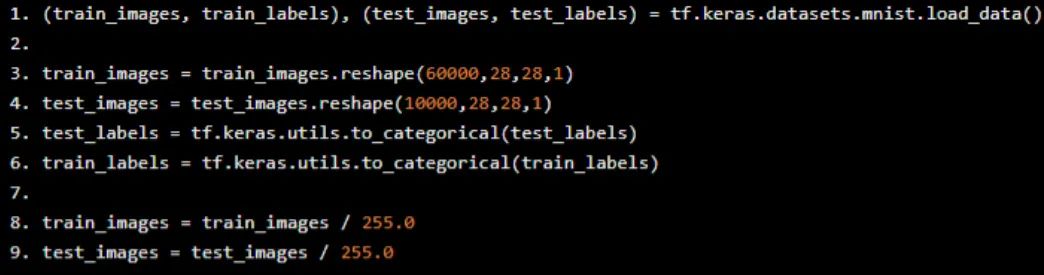
獲取數據
下一步是獲取數據。我們使用構建到Keras模塊中的機器學習數據集——MNIST數據集。在現實生活中,這需要更多的處理。
我們加載訓練和測試數據。我們reshape數據,使其更適合卷積網絡。基本上,我們將其reshape為具有60000(記錄數)大小為28x28x1的4D數組(每個圖像的大小為28x28)。這使得在Keras中構建Convolutional層變得容易。
如果我們想要一個dense 神經網絡,我們會將數據reshape為60000x784 - 每個訓練圖像的1D記錄。但CNN是不同的。請記住,卷積的概念是2D - 因此沒有必要將其flattening 為1維數組。
我們還將標簽更改為分類的one-hot數組,而不是數字分類。最后,對圖像數據進行歸一化處理,以降低梯度消失的可能性。
(train_images, train_labels), (test_images, test_labels) = tf.keras.datasets.mnist.load_data() train_images = train_images.reshape(60000,28,28,1) test_images = test_images.reshape(10000,28,28,1) test_labels = tf.keras.utils.to_categorical(test_labels) train_labels = tf.keras.utils.to_categorical(train_labels) train_images = train_images / 255.0 test_images = test_images / 255.0
?
?

構建模型
Keras庫為我們提供了準備使用API來構建我們想要的模型。我們首先創建Sequential模型的實例。然后,我們將層添加到模型中。第一層是卷積層,處理28x28的輸入圖像。我們將核大小定義為3并創建32個這樣的核 - 創建32 frames?的輸出 - 大小為26x26(28-3 + 1 = 26)
接下來是2x2的最大池化層。這將尺寸從26x26減小到13x13。我們使用了最大池化,因為我們知道問題的本質是基于邊緣 - 我們知道邊緣在卷積中顯示為高值。
接下來是另一個核大小為3x3的卷積層,并生成24個輸出frames。每frame的大小為22x22。接下來是卷積層。最后,我們將這些數據flatten 并將其輸入到dense 層,該層具有對應于10個所需值的輸出。
model = Sequential() model.add(Conv2D(32, kernel_size=3, activation='relu', input_shape=(28,28,1))) model.add(MaxPooling2D(pool_size=(3, 3))) model.add(Conv2D(24, kernel_size=3, activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Flatten()) model.add(Dense(10, activation='softmax')) model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
訓練模型
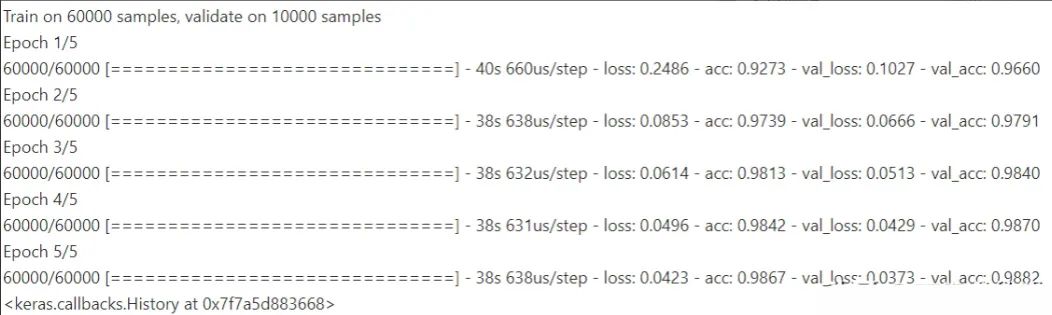
最后,我們用我們擁有的數據訓練機器學習模型。五個epochs足以獲得一個相當準確的模型。
model.fit(train_images, train_labels, validation_data=(test_images, test_labels), epochs=5)
?
最后
?
上面的模型只有9*32 + 9*24 = 504個值需要學習。全連接網絡在第一層本身需要每個神經元784個權重!因此,我們大大節省了處理能力 - 同時降低了過度擬合的風險。請注意,我們使用了我們所知道的,然后訓練模型來發現其余部分。使用全連接或隨機稀疏網絡的黑盒方法永遠不會以這個成本獲得這樣的準確性。
審核編輯:黃飛
?
 電子發燒友App
電子發燒友App






























評論