作者?|?王嘉寧?
整理?|?NewBeeNLP
現如今很多大模型都開始支持超過4096長度的推理,例如GPT-4支持超過30k,ChatGLM2-6B也支持最長為32K的文本。但是由于顯存資源的限制,這些大模型在真正在訓練過程中不一定要訓練這么長的文本,通常在預訓練時只會設計到4k左右。
因此 如何確保在模型推理階段可以支持遠遠超過預訓練時的長度 ,是目前大模型的核心問題之一,我們將這一問題歸為 大模型的外推性 。
大模型的外推性目前主要在這兩個方面考慮,也是提升最有效的兩個角度:
尋找或設計合適的位置編碼;
設計局部注意力機制。
本文從這兩方面進行深度探討大模型的位置編碼和外推性問題。
一、位置編碼基礎介紹
對于一個token ,其表征向量記作 ,對于一個句子 則表示為 。那么可以通過一個映射函數將這個句子中的token表征為 :
其中 和 表示第 和第 個token。
1.1 絕對位置編碼
在Transformer中,采用正余弦函數來表示絕對位置,公式如下:
這種編碼方式又叫做 Sinusoidal編碼 。直覺上看,第個位置的表征向量維度是 ,這個向量的奇數位置元素使用余弦值,偶數位置元素使用正弦值。
可視化圖如下所示:
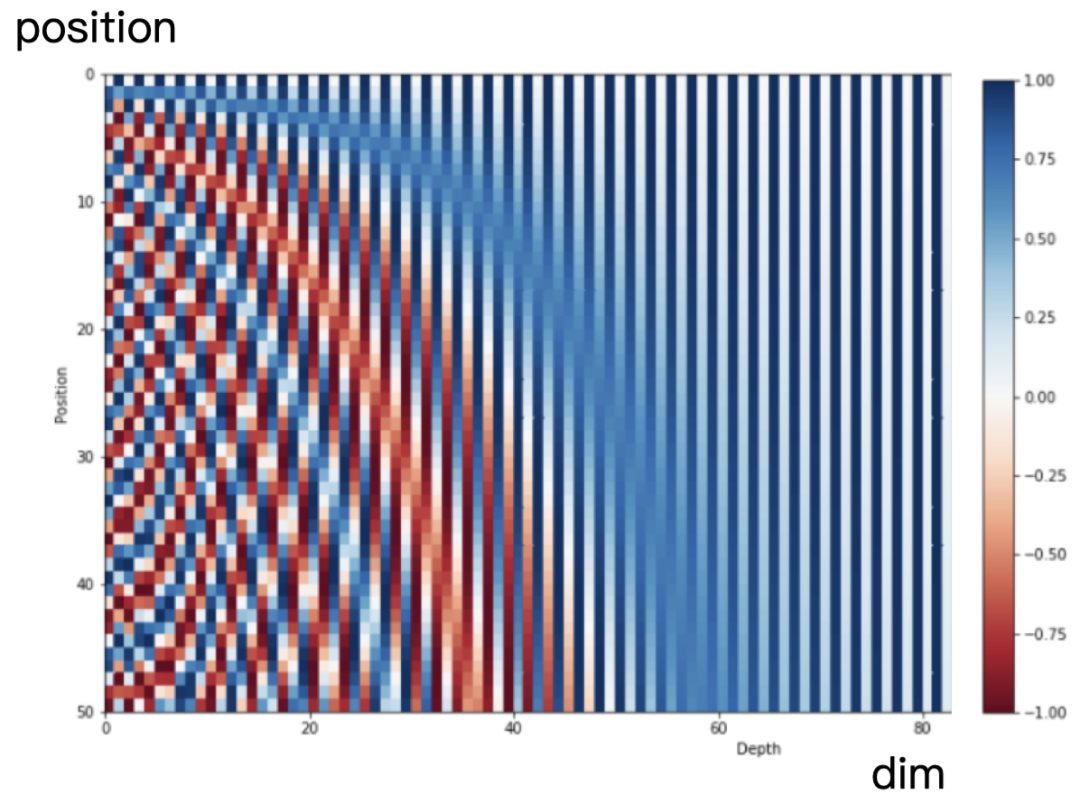
相鄰的位置編碼向量很相似,較遠的位置編碼向量差異很大,說明基于正余弦函數的絕對位置可以表征位置的相關性;
不需要顯式地學習位置,提高效率。
最后 映射函數可以定義如下所示。即輸入表征為token的表征和其對應的絕對位置表征。
該表征通常是直接將位置表征與Word表征直接相加。
1.2 相對位置編碼
(1)顯式的相對位置
對于第 和第 個位置的token,其相對位置可以表示為,即兩個token之間的相對距離,且由最大最小值做約束(相對位置不能超過最大值或小于最小值)。
因此,相比于絕對位置,相對位置只需要有表征向量即可,即在計算兩個token之間的attention值時,只需要在attention計算過程中注入這兩個位置對應的相對位置 對應的相對位置表征向量即可:
這樣一來,只需要有限個位置編碼,就可以表達出任意長度的相對位置(因為進行了截斷),不管是選擇可訓練式的還是三角函數式的,都可以達到處理任意長度文本的需求。
該表征通常是直接將位置表征與Word表征直接相加。
參考論文:《Self-Attention with Relative Position Representations》
(2)Transformer-XL(XLNet)
將第 和第 個位置的QK計算進行了分解。引入了一些可學習的參數:
其中 表示待學習的第 個token的相對位置向量, 表示待學習的第 個token的相對位置向量。通過分解讓相對位置注入在attention的計算過程中。
該表征通常是在Attention計算過程中融入絕對位置。
(3)Transformer-XL的改進
第二和第四項使用相對位置表征 來替換絕對位置表征。同時加入新的可訓練參數 和 。
該表征方法在T5模型中被首次使用,參考論文:《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》
該表征通常是在Attention計算過程中融入相對位置。
(4)可訓練偏置項
Transformer-XL中的位置表征是將QK分解為4項,而后面3個夠項都有跟位置有關的參數,可以直接將后面的3項之和抽象為一個偏置:
進一步改造還可以得到:
以及:
這三種方法均是對Transformer-XL的表征形式進行改進。
二、RoPE旋轉位置編碼
RoPE(Rotary Position Embedding)的出發點就是“ 通過絕對位置編碼的方式實現相對位置編碼 ”,或者可以說是實現 相對位置編碼和絕對位置編碼的結合 。
這樣做既有理論上的優雅之處,也有實踐上的實用之處,比如它可以拓展到線性Attention中就是主要因為這一點。
2.1 復數的引入
假設 和 是對應位置的二維行向量(即每個位置都有兩個向量來表征位置),因此這個二維向量可以用復數來代替(包括實部和虛部),因此他們的內積可以作為其對應的Attention值。
內積的計算可以由兩個復數實現:,其中 表示共軛復數, 表示取復數中的實部。
兩個二維向量的內積,等于把它們當復數看時,一個復數與另一個復數的共軛的乘積的實部。
因此當分別對 和 融入絕對位置時,即得到:
RoPE求解過程推導了如何確定獲得每個位置編碼是 。
可以發現,當乘以絕對位置 和 時,等價于復數運算中乘以 ,即相當于在復數空間中是相對位置 ,這樣就巧妙地通過復數運算的形式將絕對位置轉換為相對位置。
復數乘法的幾何意義是向量的旋轉,假設 表示向量 在位置的位置編碼,則有:
其中
等價于
后面兩項的乘積本質就是向量 (或)的兩個二維行向量。
當向量維度為 時( 為偶數),則可以擴展為:
每兩個為一組二維向量,一共有 個組合,可以直接拼接作為維度的旋轉位置編碼。
二維擴展到多維的解讀:Transformer升級之路:4、二維位置的旋轉式位置編碼 - 科學空間|Scientific SpacesTransformer升級之路:6、旋轉位置編碼的完備性分析 - 科學空間|Scientific Spaces
2.2 RoPE的實現
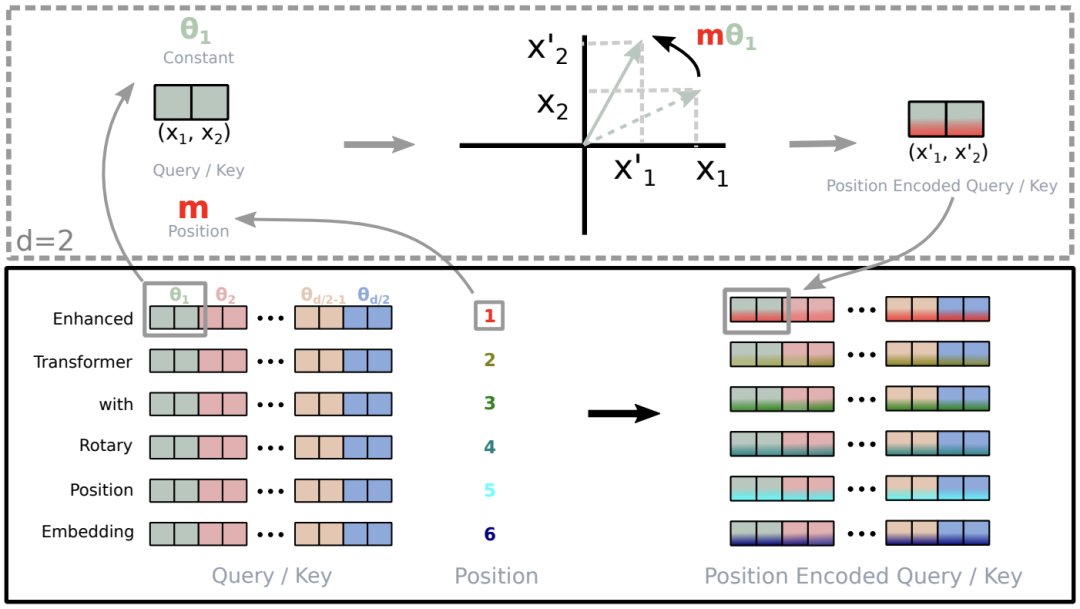
當輸入一個句子“Enhanced Transformer with Rotary Position Embedding”時,首先獲得其Query和Key向量q、 k,其對應的維度均為d,然后對于向量中相鄰兩個元素為一組,可以得到 d/2組(圖中左下部分相同顏色的兩個元素作為一組,對于每一組,一個文本則可以得到兩個行向量);
獲得每個詞的絕對位置編號(該句子由6個詞,位置編號分別為1,2,3,4,5,6),假設取“Enhanced”單詞為例,其第一組元素為θ1,位置為 m=1,那么通過旋轉位置編碼可以的到新的元素值。
所有單詞的d/2個組合都按照這種形式進行“旋轉”,即可得到新的位置編碼(右下角)
RoPE一種線性的實現如下所示:
RoPE的性質
(1)遠程衰減
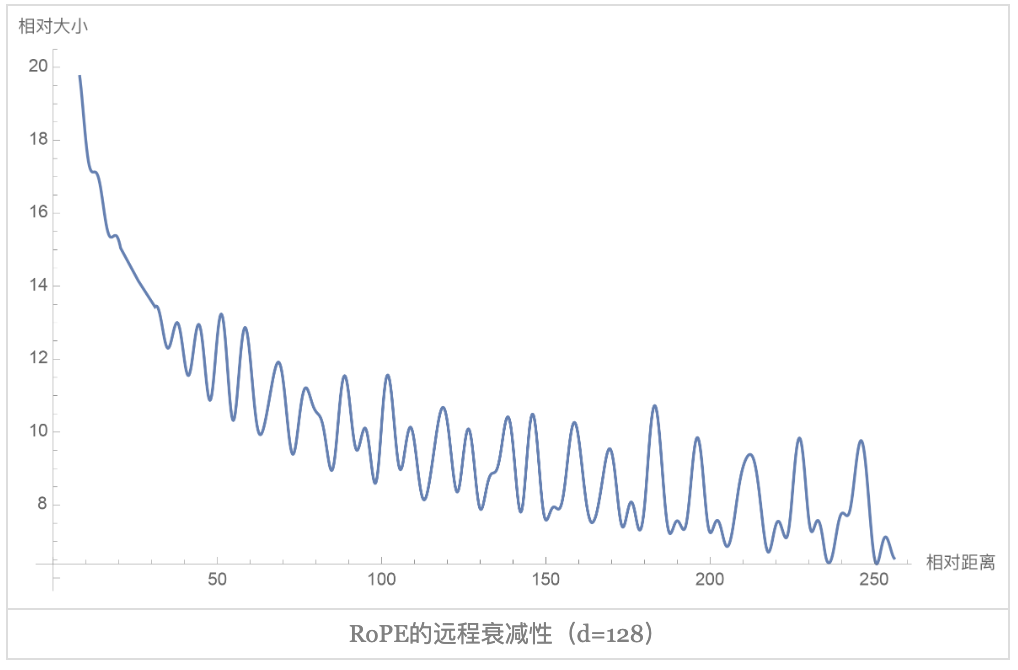
從圖中我們可以可以看到隨著相對距離的變大,內積結果有衰減趨勢的出現。因此,選擇,確實能帶來一定的遠程衰減性。當然,能帶來遠程衰減性的不止這個選擇,幾乎任意的光滑單調函數都可以。如果以為初始化,將視為可訓練參數,然后訓練一段時間后發現并沒有顯著更新,因此干脆就直接固定了。
(2)優勢
用一個旋轉矩陣rotation matrix來對絕對位置進行編碼,于此同時,meanwhile;
在自注意力機制中導入顯式的位置依賴。
自由的序列長度;
隨著相對位置的增大,而逐步延緩退化(=衰減)的inter-token dependency;
用相對位置編碼來“武裝”線性自注意力。
具體來說,RoPE 使用 旋轉矩陣對絕對位置進行編碼 ,同時將 顯式的相對位置依賴性納入自注意公式中 。
【核心的兩個點,一個是“旋轉矩陣”,一個是“顯式的相對位置依賴”】。
三、長文本外推性
外推性 的含義是在長文本表征過程中,如何在訓練階段只需要學習有限的長度,即可以在推理階段能夠延伸長度至若干倍且依然保持不錯的性能和效果。
長度外推性是一個訓練和預測的長度不一致的問題,主要體現在兩個方面:
預測的時候用到了沒訓練過的位置編碼(不論是絕對位置還是相對位置);
預測的時候注意力機制所處理的token數量遠超訓練時的數量。
解決長文本外推性問題的一個簡單有效的方法是Attention Mask,如圖所示:
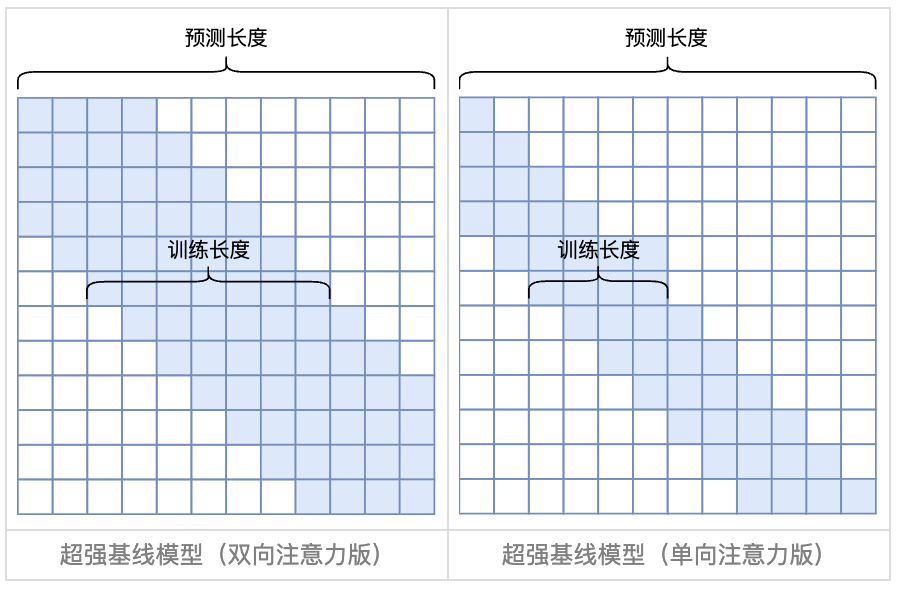
通過類似滑動窗口的結構,約束一個每個token只能對局部區域的token計算Attention值,因此對于相對位置大小不會超過窗口大小,解決了第一個問題;
Attention只會在窗口內計算,避免了對大量的token的Attention進行加權平均導致最終權重過度“平滑”現象。
在實現過程中,本質上是在計算完之后減去一個矩陣,即 ,其中的形狀如下圖所示:
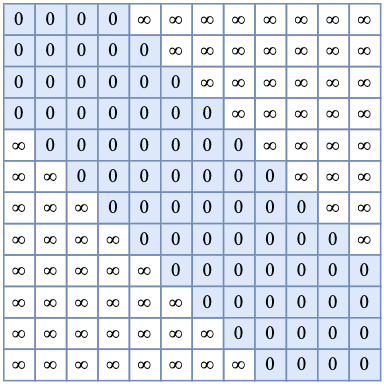
可以看出,藍色區域(即滑動窗口內的局部區域)為0,說明保持原始的Attention歸一化前的值;其他區域則為一個INT內最大的整數,說明Attention值是一個非常小的數(在softmax歸一化后幾乎為0)。
3.1 ALIBI
論文:《Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation》
其與上面的思想一樣,只是改進了上面的 M矩陣為 ,即Attention在歸一化前的計算為:,其中為超參數,Transformer的多頭注意力中的每個頭的值可設置不同。矩陣 的形狀如下所示:
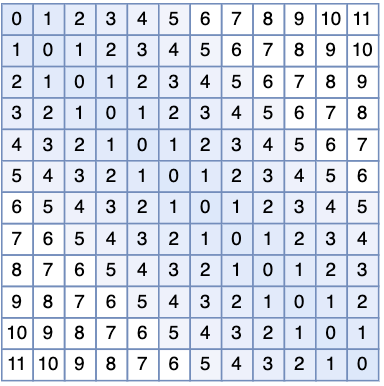
相比于原始的方法,相對距離越長,值就越大,越遠的位置Attention值被歸一化后就約小,相對于“滑動窗口”采用的方法是hard(在窗口內就計算attention,不在窗口內不計算),AIBLI是比較soft的(離得近attention就會比較大,離得遠就比較小)。
3.2 KERPLE
論文:《KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation》
其對ALIBI進行了一些改進,引入了兩個可學習的參數 和 來“動態”學習局部區域。如下圖所示,左側為原始的,通過引入參數來動態減去AIBLI中的 矩陣:
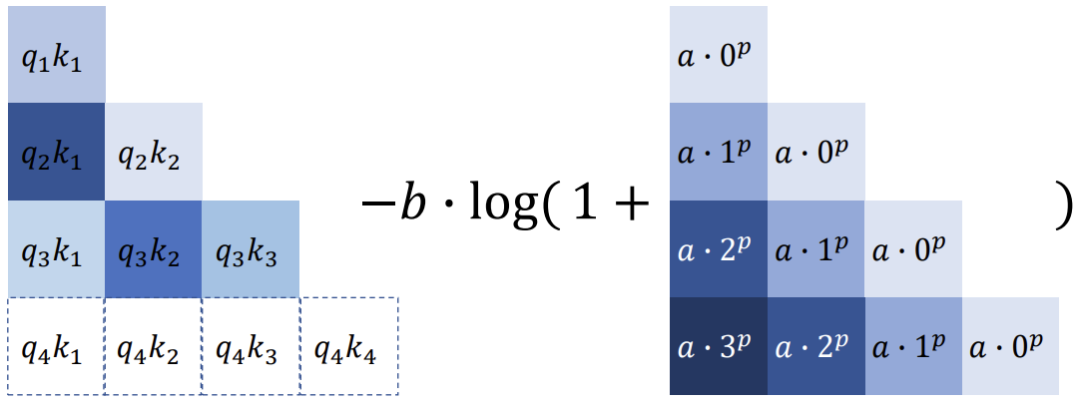
定義了兩種模式,分別是power和logarithmic,分別對應沒有對數和有對數的形式:
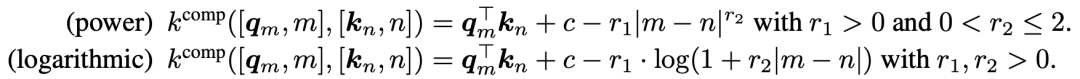
在logarithmic模式中, 控制了整體的量,相當于ALIBI中的 , c是一個常數。蘇神版簡化寫作:
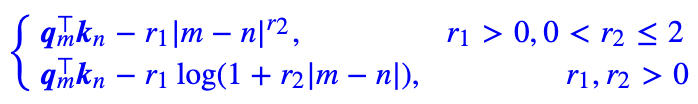
3.3 Sandwich
論文:《Receptive Field Alignment Enables Transformer Length Extrapolation》
Sandwich與KEPRLE是同一個作者提出的,其對KEPRLE進行了少量改進,即對應的公式改寫為:,其中 和 可以使用Sinusoidal編碼表示,即:
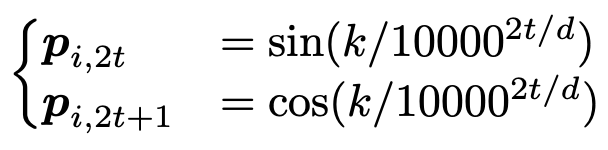
由于Sinusoidal編碼在單調性上等價于 ,都是線性遞增形式,因此Sandwich只是改頭換面了。
3.4 XPOS
論文:《A Length-Extrapolatable Transformer》
參考解讀:Transformer升級之路:7、長度外推性與局部注意力
其在RoPE的基礎上引入了局部注意力。RoPE的本質是:
其中:
在第2大節中已經介紹了RoPE是通過使用復數來實現絕對位置表示相對位置的。XPOS通過引入一個新的標量 ,即有:
由于RoPE相對位置是 ,而不是 ,因此XPOS約束在了單向Transformer,從而避免了負數出現。
XPOS又設計了一個局部感知的注意力機制Blockwise Causal Attention,進一步提升了局部注意力的性能,提升了長文本的外推性。
四、外推性的其他探索
(1)混合注意力Mask
在解決長文本位置表征時,典型的代表有Transformer-XL、BigBird、LongFormer,他們除了局部注意力機制以外,還引入了隨機位置的性質:
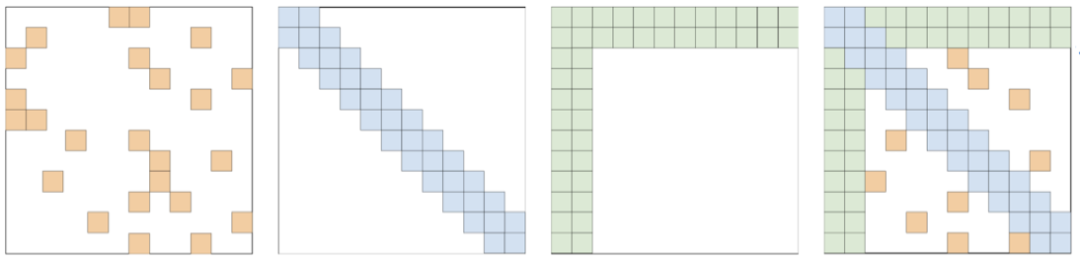
如上圖,第2張圖為局部注意力(滑動窗口),第3章圖為有限的全局感知(例如只限制前兩個token可以看見所有的token)。而第一張圖則是隨機mask,以緩解過度hard的局部注意力。三者注意力混合起來后得到第四張圖,這也是普遍訓練超長文本大模型時采用的方法。
(2)隨機位置表征
論文:《Randomized Positional Encodings Boost Length Generalization of Transformers》
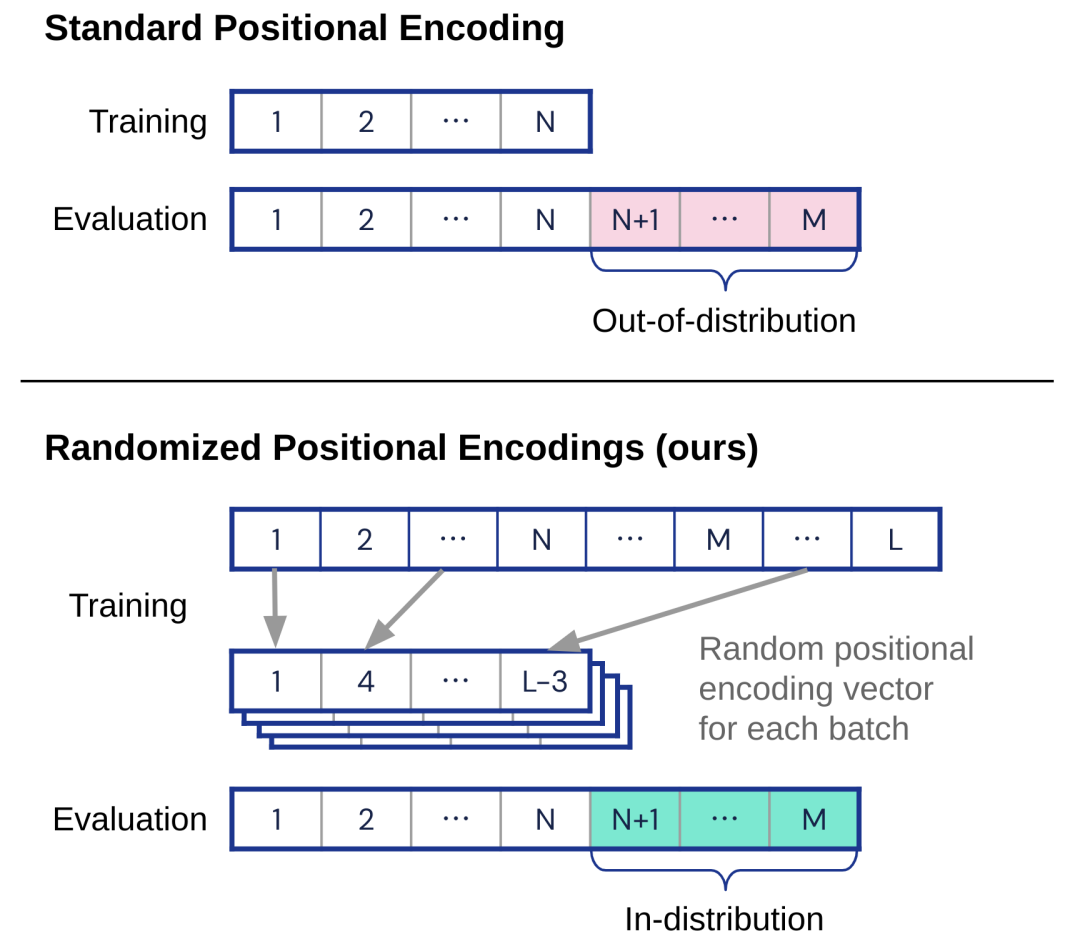
絕對位置表征時,會存在位置上的OOV問題,隨機位置編碼則是通過在訓練過程中采用如下策略:

對應的代碼也很簡單:
def?random_position_ids(N,?L=2048): ????"""從[0,?L)中隨機不重復挑N個整數,并從小到大排列 ????""" ????return?np.sort(np.random.permutation(L)[:N])
蘇神對隨機位置編碼的新探索:

對應的代碼為:
def?random_position_ids(N): ????"""先隨機采樣n,然后從[0,?n]均勻取N個點 ????""" ????n?=?sample_from_xxx() ????return?np.linspace(0,?1,?N)?*?n
(3) Attention Scale
原始的Attention計算公式為:
只需要簡單的改成下面即可:
其中 是訓練時的最大長度, 是預測時的位置,通常來說。直覺來看,就是直接在計算時,根據其相對位置來控制Attention的值。當 和距離很遠時, 的值會很大,會使得整體Attention歸一化后會比較平緩,有助于解決外推性問題。
(4)全局依賴
滑動窗口的方法如果在一層Transformer Layer里看,本質上類似長度為 的N-Gram模型,即如下圖所示:
如果Transformer又 層,那么,從輸入層開始,長度為 的窗口內的信息,可以在經過 層之后傳給一個更廣的區域,區域長度為 ,如下圖所示:
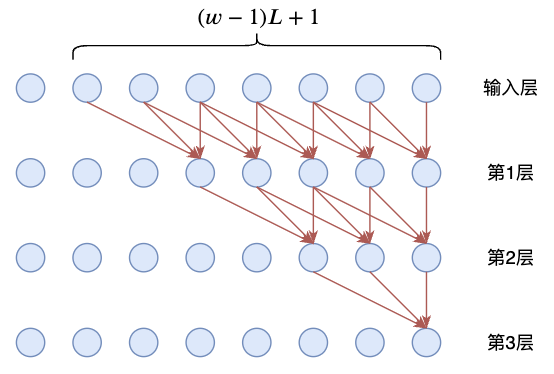
蘇神給出的一種新的想法,就是假設我有層Transformer,則可以在前 層利用這種擴張特性,得到最終 長度的區域后,在最后一層采用上面提到的 logn Attention Scale方法,講前 層擴張的信息快速在最后一層與所有token進行交互。引入蘇神的原文為:

這種局部注意力+Attention Scale的結合也是一種很巧妙的idea。實驗也發現這種策略的外推性很驚艷。
編輯:黃飛
 電子發燒友App
電子發燒友App

























評論