圖靈獎得主 Geoffrey Hinton 等研究者讓前向梯度學習變得實用了。
我們知道,在人工智能領(lǐng)域里,反向傳播是個最基本的概念。
反向傳播(Backpropagation,BP)是一種與最優(yōu)化方法(如梯度下降)結(jié)合使用的,用來訓練人工神經(jīng)網(wǎng)絡(luò)的常見方法。該方法計算對網(wǎng)絡(luò)中所有權(quán)重計算損失函數(shù)的梯度。這個梯度會反饋給最優(yōu)化方法,用來更新權(quán)值以最小化損失函數(shù)。
簡而言之,BP 的核心思路其實就是負反饋,我們試圖用這種方式實現(xiàn)神經(jīng)網(wǎng)絡(luò)系統(tǒng)面對給定目標的自動迭代、校準。隨著算力、數(shù)據(jù)和更多技術(shù)改進的提升,在 AI 領(lǐng)域人們使用反向傳播訓練的多層神經(jīng)網(wǎng)絡(luò)在部分任務上已經(jīng)足以與人類競爭。
很多人把這項技術(shù)的發(fā)現(xiàn)歸功于深度學習先驅(qū)、2019 年圖靈獎得主 Geoffrey Hinton,但 Hinton 本人表示,自己的貢獻在于明確提出了反向傳播可以學習有趣的內(nèi)部表征,并讓這一想法推廣開來:「我通過讓神經(jīng)網(wǎng)絡(luò)學習詞向量表征,使之基于之前詞的向量表征預測序列中的下一個詞實現(xiàn)了這一點。」
其例證在于 Nature 1986 年發(fā)表的論文《Learning representations by back-propagating errors》上。

無論如何,反向傳播技術(shù)推動了現(xiàn)代深度學習的發(fā)展。但曾被冠以「反向傳播之父」的 Geoffrey Hinton,近年來卻經(jīng)常表示自己在構(gòu)思下一代神經(jīng)網(wǎng)絡(luò),他對于反向傳播「非常懷疑」,并提出「應該拋棄它并重新開始」。
可以說自 2017 年起,Hinton 就已開始尋找新的方向。機器之心先前曾介紹 Hinton 在前向 - 前向網(wǎng)絡(luò)方面的思考(近萬人圍觀 Hinton 最新演講:前向 - 前向神經(jīng)網(wǎng)絡(luò)訓練算法,論文已公開)。
最近,我們又看到了重要的進展。近日,由 Mengye Ren、Simon Kornblith、Renjie Liao、Geoffrey Hinton 完成的論文被工智能頂會 ICLR 2023 接收。
前向梯度學習通常用于計算含有噪聲的方向梯度,是一種符合生物學機制、可替代反向傳播的深度神經(jīng)網(wǎng)絡(luò)學習方法。然而,當要學習的參數(shù)量很大時,標準的前向梯度算法會出現(xiàn)較大的方差。
基于此,圖靈獎得主 Geoffrey Hinton 等研究者提出了一系列新架構(gòu)和算法改進,使得前向梯度學習對標準深度學習基準測試任務具有實用性。

論文鏈接:https://arxiv.org/abs/2210.03310
GitHub 鏈接:https://github.com/google-research/google-research/tree/master/local_forward_gradient
該研究表明,通過將擾動(perturbation)應用于激活而不是權(quán)重,可以顯著減少前向梯度估計器的方差。研究團隊通過引入大量局部貪心損失函數(shù)(每個損失函數(shù)只涉及少量可學習參數(shù))和更適合局部學習的新架構(gòu) LocalMixer(受 MLPMixer 啟發(fā)),進一步提高了前向梯度的可擴展性。該研究提出的方法在 MNIST 和 CIFAR-10 上與反向傳播性能相當,并且明顯優(yōu)于之前 ImageNet 上的無反向傳播算法。
當前,大多數(shù)深度神經(jīng)網(wǎng)絡(luò)都使用反向傳播算法(Werbos, 1974; LeCun, 1985; Rumelhart et al., 1986)進行訓練,該算法通過從損失函數(shù)向每一層反向傳播誤差信號來有效地計算權(quán)重參數(shù)的梯度。盡管人工神經(jīng)網(wǎng)絡(luò)最初受到生物神經(jīng)元的啟發(fā),但反向傳播一直被認為不符合生物學機理,因為大腦不會形成對稱的反向連接或執(zhí)行同步計算。從工程的角度講,反向傳播與大規(guī)模模型的并行性不兼容,并且限制了潛在的硬件設(shè)計。這些問題表明我們需要一種截然不同的深度網(wǎng)絡(luò)學習算法。
Hinton 等研究者重新審視了權(quán)重擾動的替代方法 —— 活動擾動(activity perturbation,Le Cun et al., 1988; Widrow & Lehr, 1990; Fiete & Seung, 2006),探索了該方法對視覺任務訓練的普遍適用性。
該研究表明:活動擾動能比權(quán)重擾動產(chǎn)生方差更低的梯度估計,并且能夠為該研究提出的算法提供基于連續(xù)時間速率(continuous-time rate-based)的解釋。
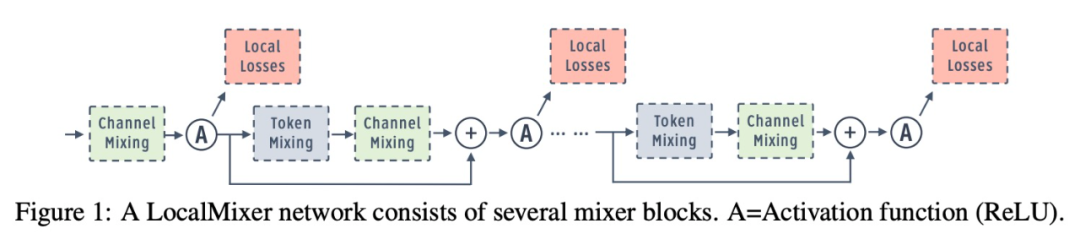
研究團隊通過設(shè)計具有大量局部貪心損失函數(shù)的架構(gòu),解決了前向梯度學習的可擴展性問題,其中將網(wǎng)絡(luò)隔離為局部模塊,從而減少了每個損失函數(shù)的可學習參數(shù)量。與僅沿深度維度添加局部損失的先前工作不同,該研究發(fā)現(xiàn) patch-wise 和 channel-group-wise 損失函數(shù)也非常關(guān)鍵。最后,受 MLPMixer (Tolstikhin et al., 2021) 的啟發(fā),該研究設(shè)計了一個名為 LocalMixer 的網(wǎng)絡(luò)。LocalMixer 具有線性 token 混合層和分組通道(channel),以更好地與局部學習兼容。
該研究在監(jiān)督和自監(jiān)督圖像分類問題上評估了其局部貪婪前向梯度算法。在 MNIST 和 CIFAR-10 上,該研究提出的學習算法性與反向傳播性能相當,而在 ImageNet 上,其性能明顯優(yōu)于其他使用不對稱前向和后向權(quán)重的方案。雖然該研究提出的算法在更大規(guī)模的問題上還達不到反向傳播算法的性能,但局部損失函數(shù)設(shè)計可能是生物學上合理的學習算法,也將成為下一代模型并行計算的關(guān)鍵因素。
該研究分析了前向梯度估計器的期望和方差的特性,并將分析重點放在了權(quán)重矩陣的梯度上,具體的理論分析結(jié)果如下表 1 所示,批大小為 N 時,獨立擾動(independent perturbation)可以將方差減少為 1/N,而共享擾動(shared perturbation)具有由平方梯度范數(shù)支配的常數(shù)方差項。然而,當執(zhí)行獨立的權(quán)重擾動時,矩陣乘法不能進行批處理,因為每個樣本的激活向量都要與不同的權(quán)重矩陣相乘。相比之下,獨立的活動擾動算法允許批量矩陣乘法。

與權(quán)重擾動相比,活動擾動的方差更小,因為擾動元素的數(shù)量是輸出單元的數(shù)量,而不是整個權(quán)重矩陣的大小。活動擾動的唯一缺點是存儲中間激活需要一定量的內(nèi)存。
此外,該研究發(fā)現(xiàn)在具有 ReLU 激活的網(wǎng)絡(luò)中,可以利用 ReLU 稀疏性來進一步減少方差,因為未激活的單元梯度為零,因此不應該擾動這些單元。
用局部損失函數(shù)進行擴展
由于擾動學習可能會遭受「維數(shù)災難」:方差隨著擾動維數(shù)的增加而增加,并且深度網(wǎng)絡(luò)中通常有數(shù)百萬個參數(shù)同時發(fā)生變化。限制可學習維度數(shù)量的一種方法是將網(wǎng)絡(luò)劃分為子模塊,每個子模塊都有一個單獨的損失函數(shù)。因此,該研究通過增加局部損失函數(shù)的數(shù)量來抑制方差,具體包括:
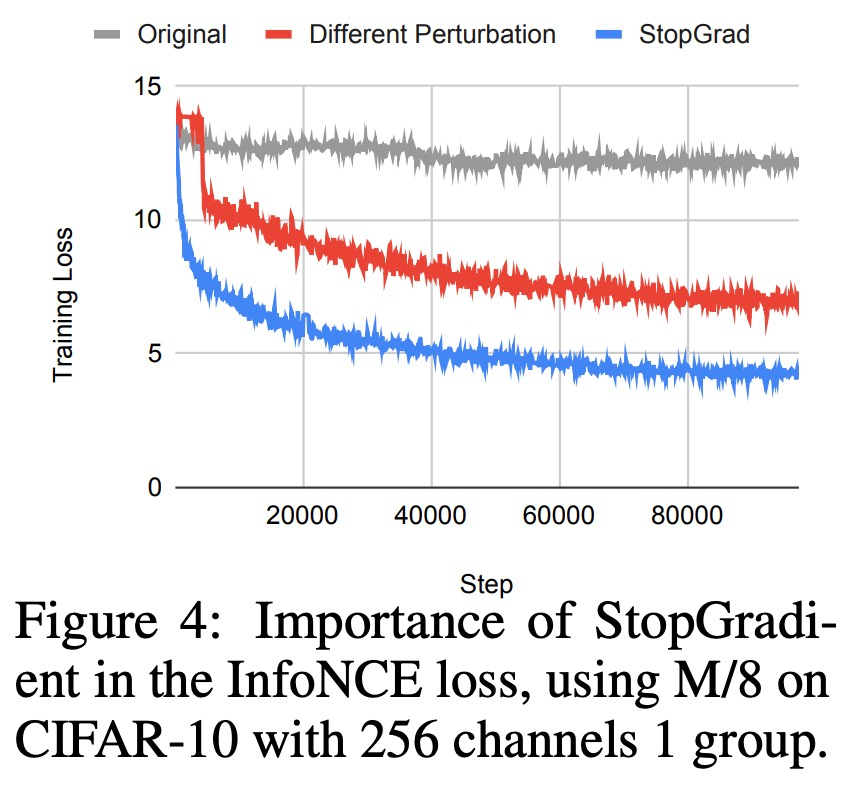
1)Blockwise 損失。首先,該研究將網(wǎng)絡(luò)深度劃分為多個模塊。每個模塊由幾個層組成,在每個模塊的末端計算一個損失函數(shù),該損失函數(shù)用于更新該模塊中的參數(shù)。這種方法相當于在模塊之間添加了一個「停止梯度(stop gradient)」算子,Belilovsky et al. (2019) 和 L?we et al. (2019) 曾探索過這種局部貪心損失函數(shù)。
2)patchwise 損失。圖像等感官輸入信號具有空間維度。該研究沿著這些空間維度,逐塊應用單獨的損失。在 Vision Transformer 架構(gòu)中(Vaswani et al., 2017; Dosovitskiy et al., 2021),每個空間標記代表圖像中的一個 patch。在現(xiàn)代深度網(wǎng)絡(luò)中,每個空間位置的參數(shù)通常是共享的,以提高數(shù)據(jù)效率并降低內(nèi)存帶寬利用率。雖然簡單的權(quán)重共享在生物學上是不合理的,但該研究仍然在這項工作中考慮共享權(quán)重。通過在 patch 之間添加知識蒸餾 (Hinton et al., 2015) 損失來模擬權(quán)重共享的效果是可能的。
3) Groupwise 損失。最后,該研究轉(zhuǎn)向通道(channel)維度。為了創(chuàng)建多個損失,該研究將通道分成多個組,每個組都附加到一個損失函數(shù)(Patel et al., 2022)。為了防止組之間相互通信,通道僅連接同一組內(nèi)的其他通道。
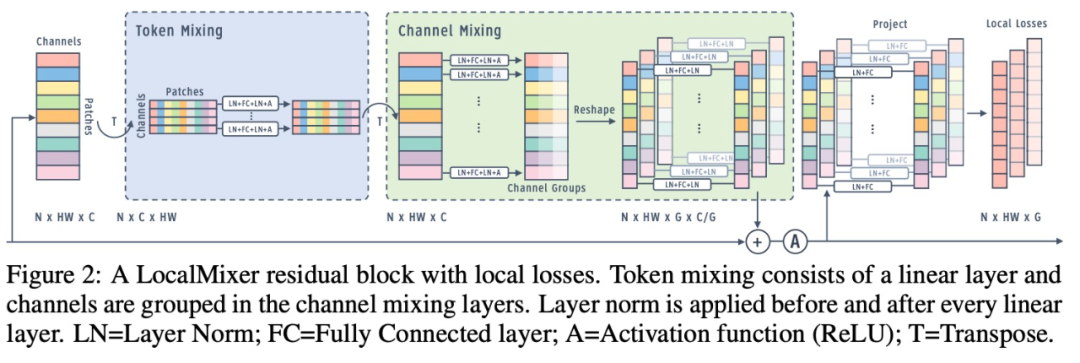
具有局部損失的 LocalMixer 殘差塊。
特征聚合器
簡單地將損失分別應用于空間和通道維度,會帶來次優(yōu)性能,因為每個維度僅包含局部信息。對于分類等標準任務的損失,模型需要輸入的全局視圖來做出決策。標準架構(gòu)通過在最終分類層之前執(zhí)行全局平均池化層,來獲得此全局視圖。因此,該研究探索了在局部損失函數(shù)之前聚合來自其他組和空間塊的信息的策略。
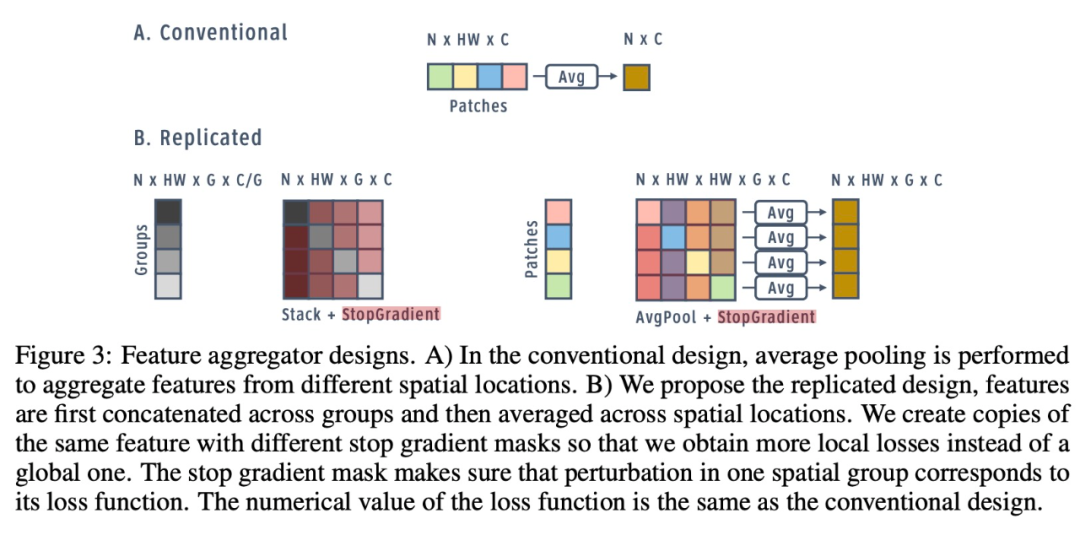
特征聚合器設(shè)計。
實現(xiàn)
網(wǎng)絡(luò)架構(gòu):該研究提出了更適合局部學習的 LocalMixer 架構(gòu)。它的靈感來自 MLPMixer (Tolstikhin et al., 2021),它由全連接網(wǎng)絡(luò)和殘差塊組成。該研究利用全連接網(wǎng)絡(luò),使每個空間塊在不干擾其他 patch 的情況下執(zhí)行計算,這更符合局部學習目標。圖 1 顯示了高級架構(gòu),圖 2 顯示了一個殘差塊的詳細圖。
歸一化。在跨不同張量維度的神經(jīng)網(wǎng)絡(luò)中執(zhí)行歸一化的方法有很多種(Krizhevsky et al., 2012; Ioffe & Szegedy, 2015; Ba et al., 2016; Ren et al., 2017; Wu & He, 2018)。該研究選擇了層歸一化的局部變體,它在每個局部空間特征塊內(nèi)進行歸一化(Ren et al., 2017)。對于分組的線性層,每組單獨進行歸一化(Wu & He, 2018)。
該研究通過實驗發(fā)現(xiàn)這種局部歸一化在對比學習中表現(xiàn)更好,并且與監(jiān)督學習中的層歸一化大致相同。局部歸一化在生物學上也更合理,因為它不執(zhí)行全局通信。
通常,歸一化層放置在線性層之后。在 MLPMixer(Tolstikhin et al., 2021)中,層歸一化被放置在每個殘差塊的開頭。該研究發(fā)現(xiàn)最好在每個線性層之前和之后放置歸一化,如圖 2 所示。實驗結(jié)果表明,這種設(shè)計選擇對反向傳播沒有太大影響,但它允許前向梯度學習更快地學習并實現(xiàn)更低的訓練錯誤。
有效實施復制損失。由于特征聚合和復制損失的設(shè)計,組(groups)的簡單實現(xiàn)在內(nèi)存消耗和計算方面可能非常低效。然而,每個空間組實際上計算相同的聚合特征和損失函數(shù)。這意味著在執(zhí)行反向傳播和正向梯度時,可以跨損失函數(shù)共享大部分計算。該研究實現(xiàn)了自定義 JAX JVP/VJP 函數(shù)(Bradbury et al., 2018)并觀察到顯著的內(nèi)存節(jié)省和復制損失的計算速度提升,否則這在現(xiàn)代硬件上運行是不可行的,結(jié)果如下圖所示。
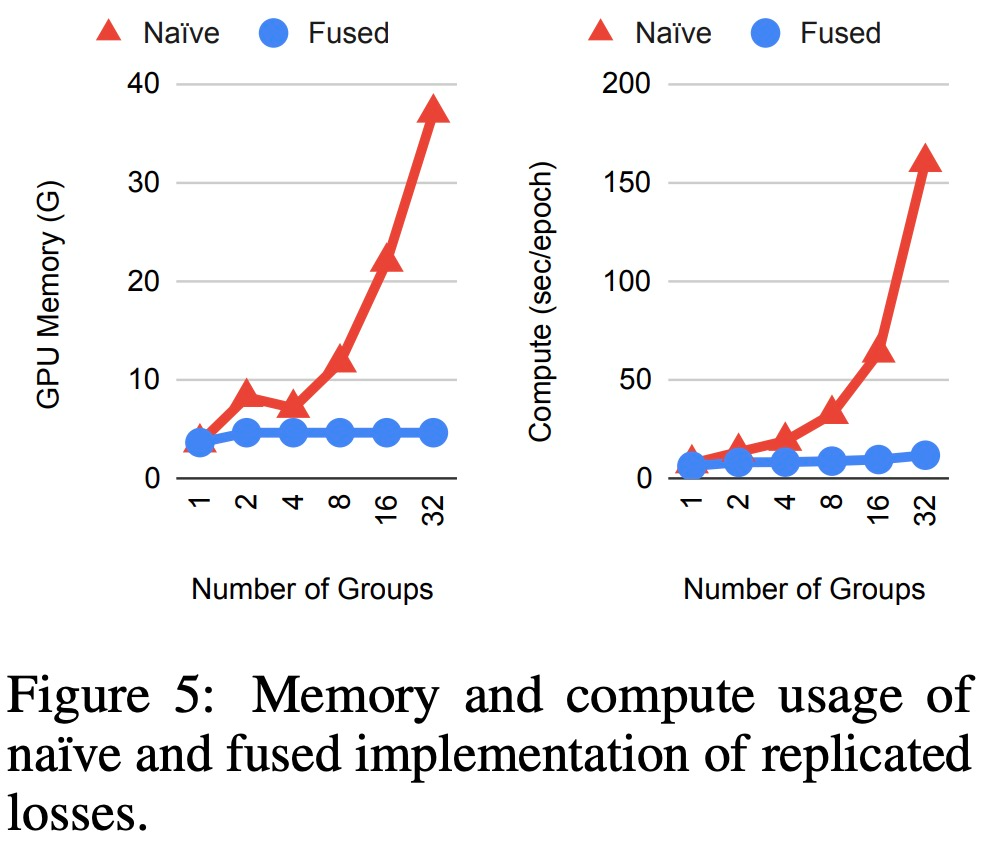
復制損失的簡單和融合實現(xiàn)時,內(nèi)存和計算使用情況。
實驗
該研究將提出的算法與包括反向傳播、反饋對齊和其他前向梯度全局變體在內(nèi)的替代方案進行比較。反向傳播是生物學上難以置信的神諭,因為它計算的是真實梯度,而該方法計算的是噪聲梯度。反饋對齊通過使用一組隨機向后權(quán)重來計算近似梯度。
各項實驗的結(jié)果如下:
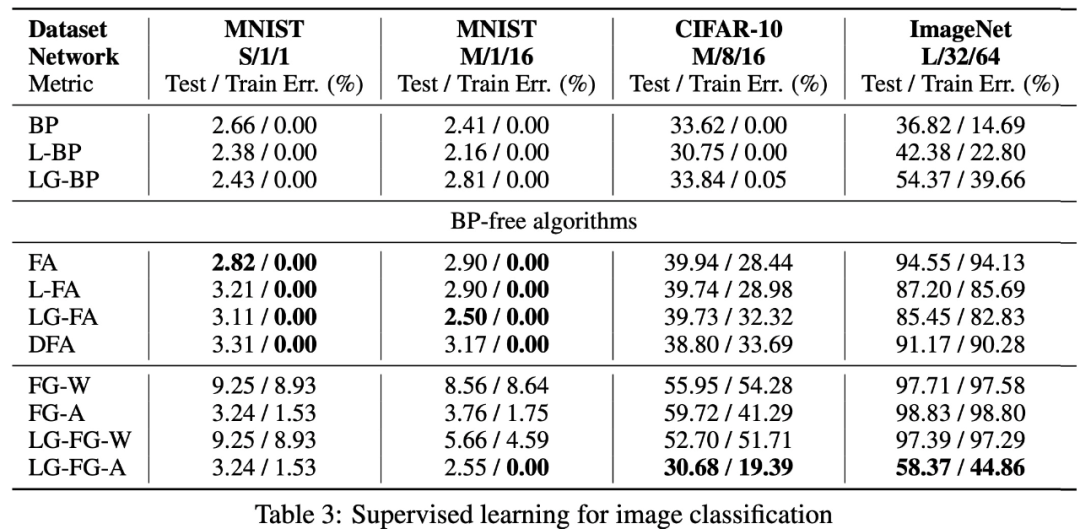
圖像分類自監(jiān)督學習。
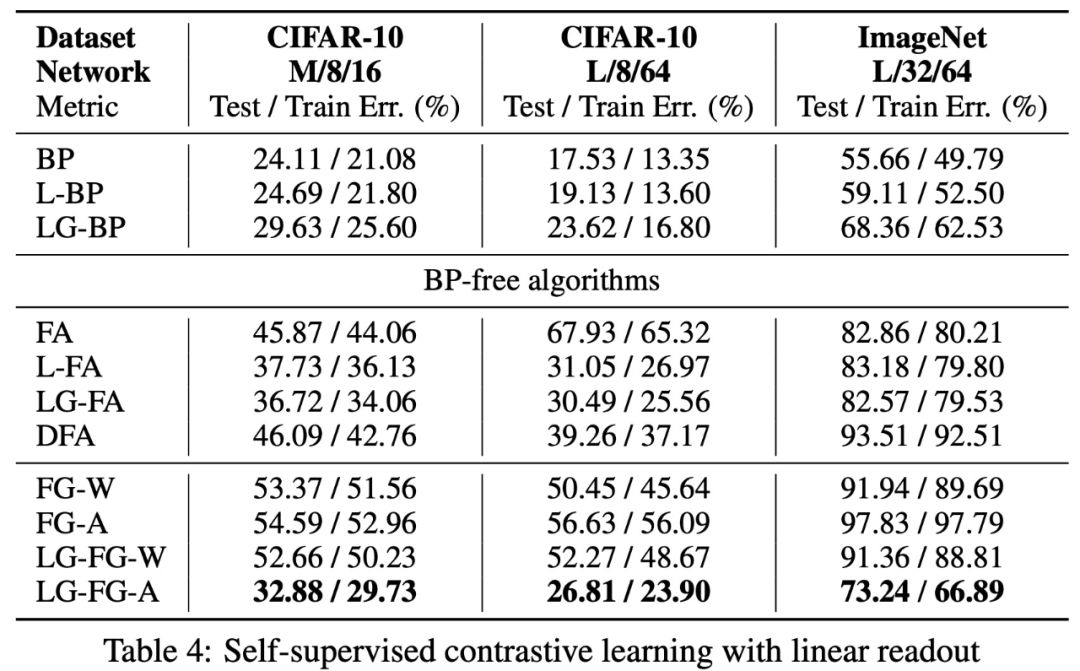
有線性 readout 的自監(jiān)督對比學習。
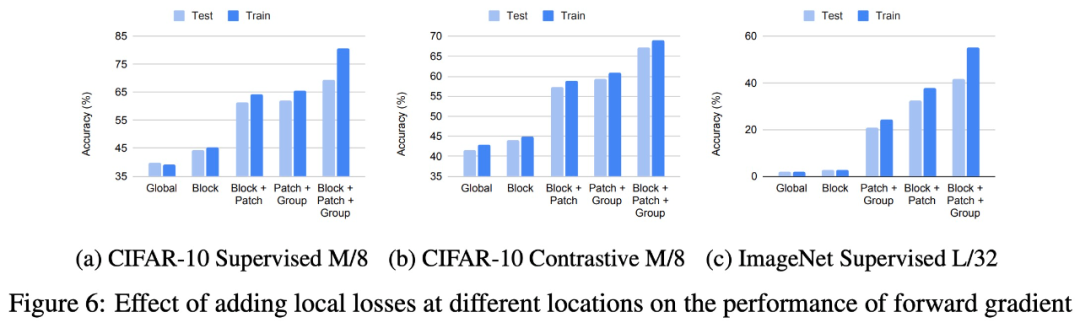
在不同位置添加局部損失對前向梯度性能的影響。
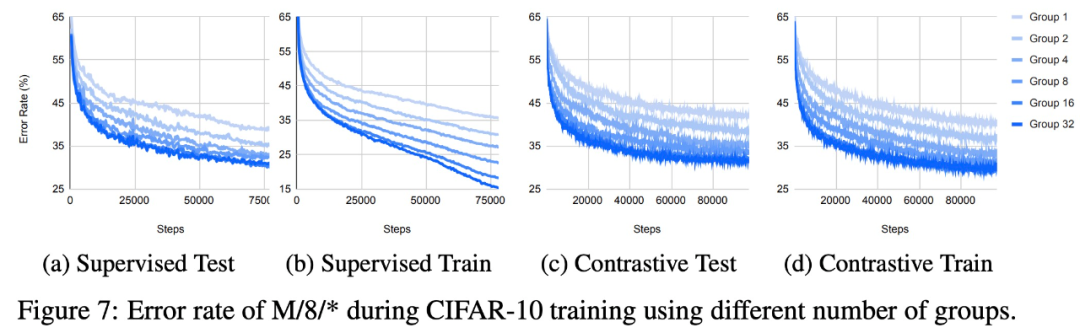
使用不同數(shù)量組時,在 CIFAR-10 上訓練時 M/8/* 的錯誤率。
總結(jié)
人們通常認為基于擾動的學習無法擴展到大型深度網(wǎng)絡(luò)。該研究表明,這在某種程度上是正確的,因為梯度估計方差隨著擾動隱藏維度的數(shù)量而增長,并且對共享權(quán)重擾動而言甚至更遭。
但樂觀的是,該研究表明大量的局部貪心損失可以幫助更好地推進梯度學習規(guī)模,探索了 blockwise、patchwise 以及 groupwise 以及這三者組合的局部損失,在一個較大的網(wǎng)絡(luò)中總共有四分之一的損失,表現(xiàn)最好。局部活動擾動前向梯度在更大的網(wǎng)絡(luò)上比以前的無反向傳播算法表現(xiàn)更好。局部損失的想法為不同的損失設(shè)計開辟了機會,并闡明了如何在大腦和替代計算設(shè)備中尋找生物學上合理的學習算法。
編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App


















評論