專家、醫生和科學家表示，為了限制冠狀病毒感染，人們在社交接觸中應保持至少 1 米的人際社交距離。但是，獨自呆在家里，被感染的風險為零。本文不打算談論有關冠狀病毒的醫學或科學新聞。它將提出一種替代算法，用于在明確定義的區域內進行人員分布，以使他們盡可能遠離。顯然，所提出的方法不是解決問題的最佳解決方案之一；它基于蒙特卡洛系統。該系統提供了一種最簡單的人員分配方式。

目標
該程序的最終目標是將一定數量的人放置在特定的空間中，使他們之間的距離足夠遠，以避免病毒傳播的風險。可用空間由一個網格或 N × M 方陣表示。人由同一網格上的標記表示。為了實現這一目標，有許多方法和許多數學和 IT 程序。無論如何，它是一個旨在最大化人與人之間距離的系統。該問題可以通過使用線性規劃系統、非線性規劃系統、遞歸算法或使用蒙特卡羅研究來解決。顯然，后者不能確保出色的結果，但對于大多數應用程序來說，它是更復雜和要求更高的程序的有效替代方案。

蒙特卡洛方法
蒙特卡洛方法是一種基于隨機抽樣獲得數值結果的計算方法。它用于通過模擬獲得估計。它基于一種算法，該算法生成一系列彼此不相關的隨機數，這些隨機數遵循這種現象的可能分布。

網格
為了表示空間上的人，我們可以使用由許多單元格組成的 2D 網格 (N × M)。我們可以將網格或矩陣想象成一個棋盤，上面放置了一些人或物體（圖 1）。網格按行和列組織，因此任何編程語言都可以輕松管理它。組織、填充、滾動和查詢矩陣相對容易。為了獲得這些結果，我們可以使用兩個嵌套的迭代循環和一些“if”條件。網格（方陣）代表人們可以在上面的有用空間。每個單位對應1米；因此，每邊10個方格組成的網格相當于100平方米的面積。該算法考慮了一個人和另一個人之間的傾斜距離。在橫向位置的情況下，將使用勾股定理計算距離。

圖 1：網格類似于棋盤，棋子必須放在盡可能遠的位置。

我們可以使用什么編程語言？
這是計算機程序員最關鍵的問題之一。有數百種編程語言，每種都有其優點和缺點。我們算法面臨的問題與研究有關。這是一個涉及數十億次迭代的蠻力程序。很明顯，為了我們的目的，必須使用一種速度極快的編程語言。可以使用更簡單、更圖形化的語言更好地以圖形格式表示最終信息，但我們決定考慮速度和性能方面，以涵蓋執行期間的最高計算次數。此外，為了提供通用代碼，我們更喜歡使用適用于任何環境和任何操作系統的 C 語言。

算法
該過程的算法非常簡單（圖 2）。令人驚訝的不是真正的方法，而是代碼執行的大量工作。實際上，在無限循環中，地圖不斷被破壞和重建以尋找最佳解決方案。C 語言的速度有助于實現更實用、更強大的搜索。代碼執行以下階段：變量和函數的準備以及主函數的執行。在其中，循環執行以下任務：重置網格，在網格上隨機放置人口，以及確定（打印）最佳距離。所有這些工作都以非常高的速度進行。

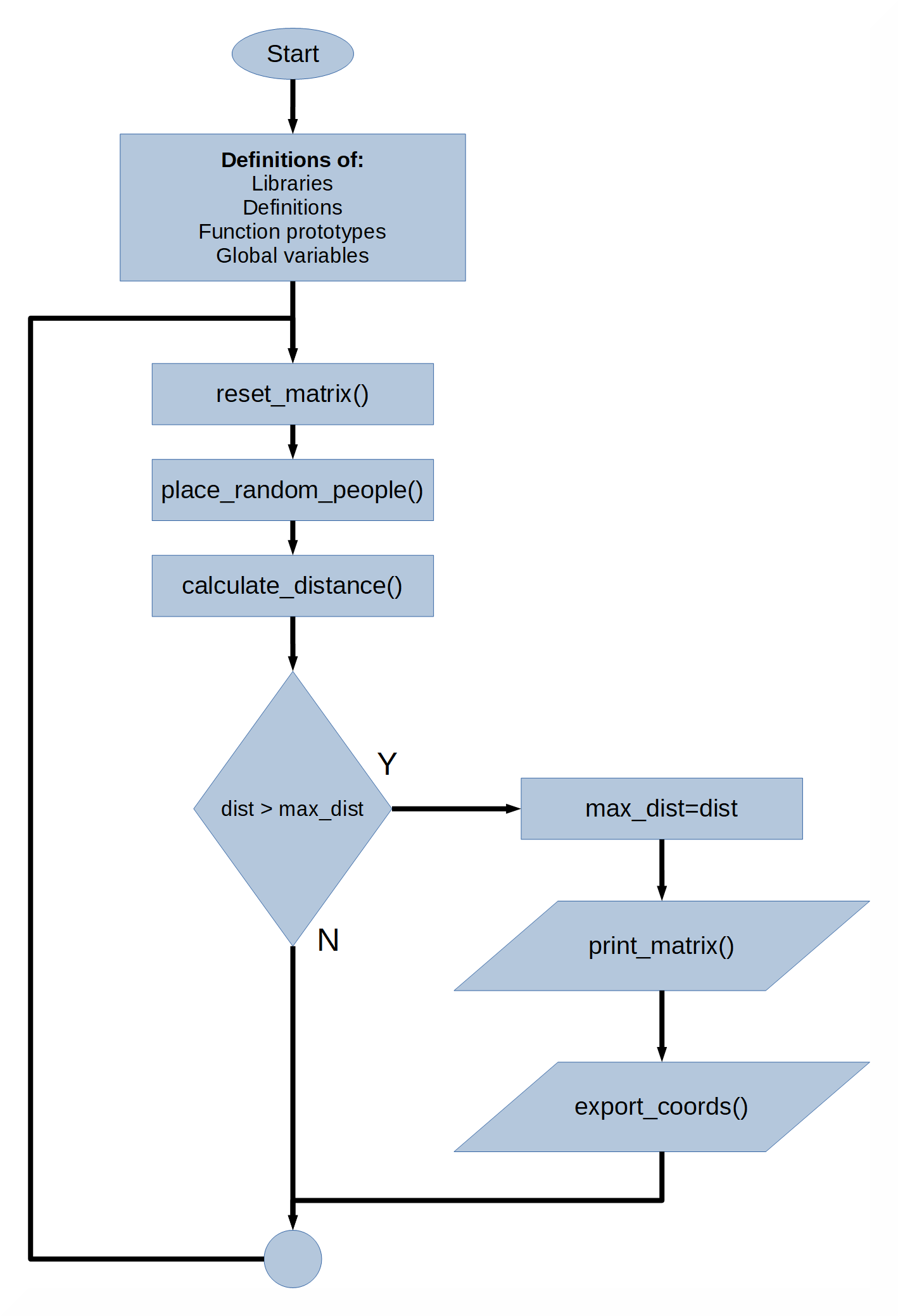
圖 2：程序流程圖

軟件
您將找到本文所附的程序源代碼 (.C)。它分為幾個邏輯部分。它從包含文件開始，其中加載了軟件中使用的函數的原型，例如在數學庫中。然后我們可以找到列數、行數、人數等全局值的定義。這些值在整個程序中是全局可見的。用戶可以自由修改這三個值（圖 3），但重要的是要記住，如果值太高，搜索時間會受到影響。

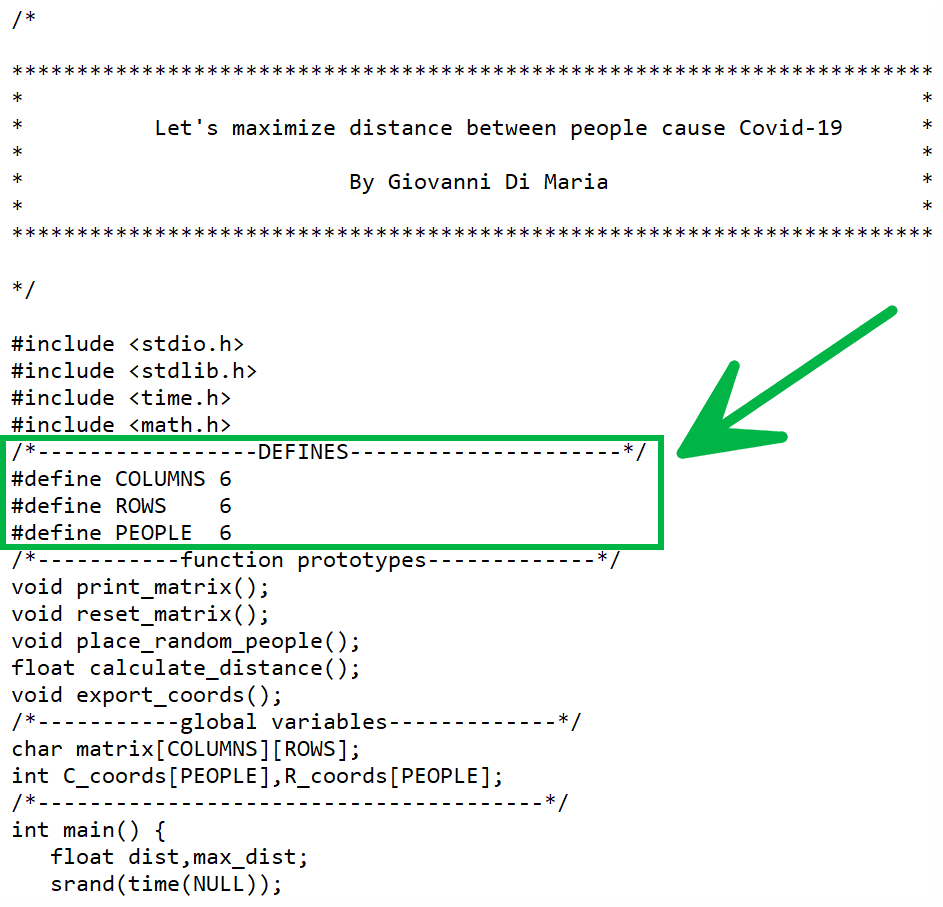
圖 3：您可以修改三個定義來改變研究領域。

程序的下一部分包含函數的原型。然后我們可以看到全局變量的定義。最后，“main()”函數開始。它包含一個非常短的無限循環，其中重復以下功能：

電網重置；

人口的隨機分布；

計算最佳距離；

確定最佳結果的可視化；

將結果導出到 Octave。

這些任務被循環和無限期地執行，因為它們包含在“while”循環中。源代碼中使用了以下 UDF 函數：

第一個函數是“print_matrix()”。它在屏幕上顯示矩陣。

下一個 UDF 函數是“reset_matrix()”。它使用雙嵌套循環將存儲“-”字符的網格歸零。

下一個函數是“place_random_people()”。它將人置于矩陣內。條件控制確保良好的定位并在單元格已被人占用時丟棄隨機數，重復提取。

下一個 UDF 浮點函數是“calculate_distance()”。它計算兩點之間的距離。它計算并返回人與人之間的最小距離。注意，如果點是傾斜排列的，軟件使用勾股定理來計算相對距離。

下一個函數“export_coords()”將數據導出到 Octave 數學環境，以優雅地顯示結果。

添加特定功能后，軟件總是會生成不同的隨機序列。事實上，在清單的開頭插入以下語句就足夠了：

srand (時間 (NULL));

通過消除這條指令，生成的數字的順序總是相同的，這對調試程序很有用。目前，該程序會找到人與人之間的最小距離，因此會最大化這個數字。要在代碼中實現的其他標準可以如下：

最小距離的最大化

平均距離最大化

不同區域的距離最大化

編譯
編譯源代碼很容易。您無需修改代碼即可將源代碼與其他編譯器一起使用。如下圖，根據使用的編譯器，可以找到一些編譯的例子。一些解決方案為速度優化提供支持：

海合會

gcc distance.c -Wall -O3

TCC

tcc 距離.c

橙色 C/C++ 編譯器

occ 距離.c

實驗
我們已準備好嘗試該程序。第一個要進行的測試涉及小范圍內的幾個人。要設置的值是：

/*——————定義——————*/

#define 列 6

#define 行 6

#定義人 6

使用命令“distance.exe”啟動程序執行后，我們將在監視器上看到第一個結果，顯示網格上人員的最佳配置（圖 4）。如果計算機找到更好的結果，這些結果將顯示在屏幕上并作為新的解決方案呈現。這些解決方案尋找人與人之間的最大距離。

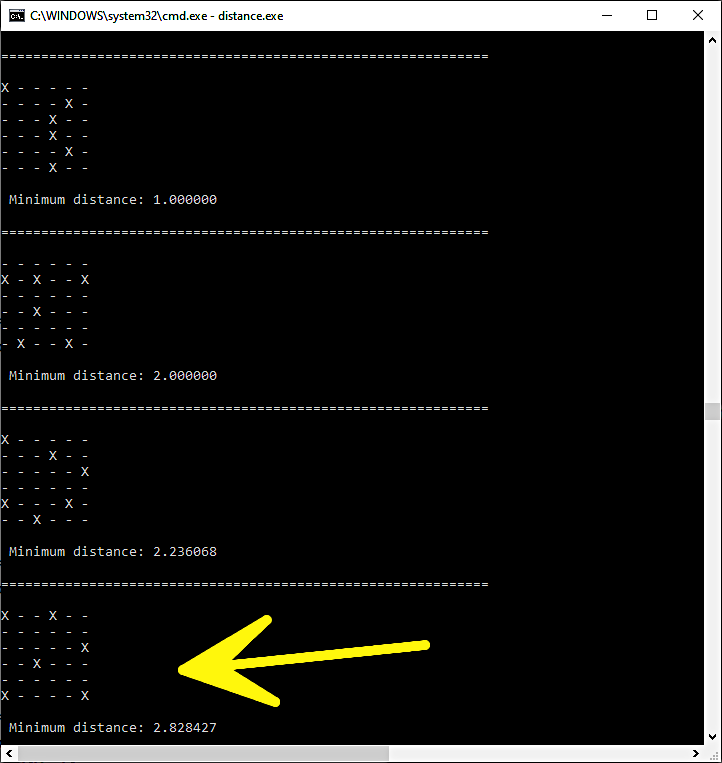
圖 4：6 人的 6 × 6 網格的解決方案

更強大的實驗可以在更大的區域內使用更多的人進行。下一個實驗應具有以下值：

/*——————定義——————*/

#define 列 20

#define 行 10

#定義人 16

在這種情況下，處理步驟更重。解決方案的顯示速度要慢得多，而且不是最好的。圖 5顯示了一種可能的解決方案，但不是最佳解決方案。

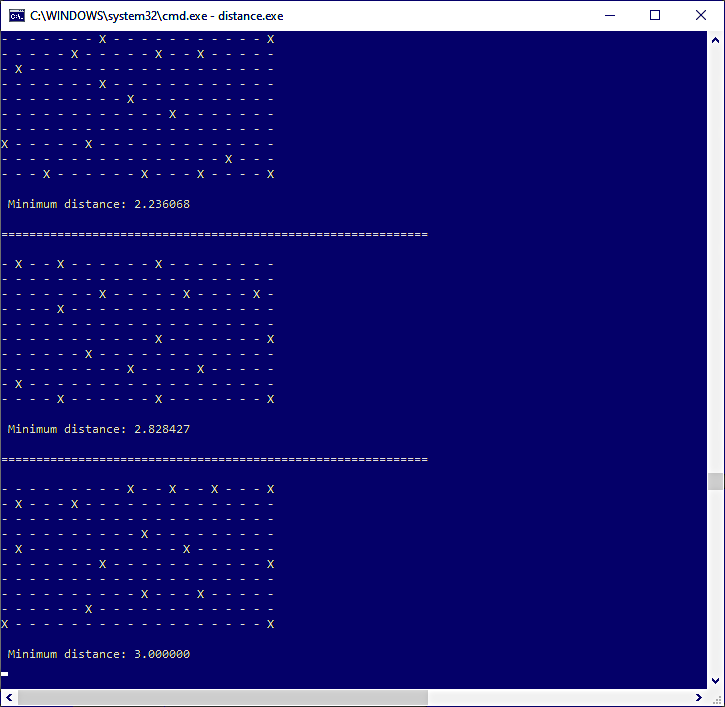
圖 5：16 人的 20 × 10 網格的解決方案

變化
兩個人之間的距離可以用不同的方式和許多標準來衡量（圖 6）。一種方法是將距離計算為理論矩形三角形的斜邊，如果人們傾斜排列的話。這種計算是最真實的，因為它通常以這種方式發生。

d = sqrt([cat1 × cat1] + [cat2 × cat2]);

另一種方法將距離視為兩個人之間的平方數。在這種情況下，人的位置是直角還是斜角都沒有區別。

d = abs(cat1) + abs(cat2);

程序員可以選擇計算距離的首選方法。

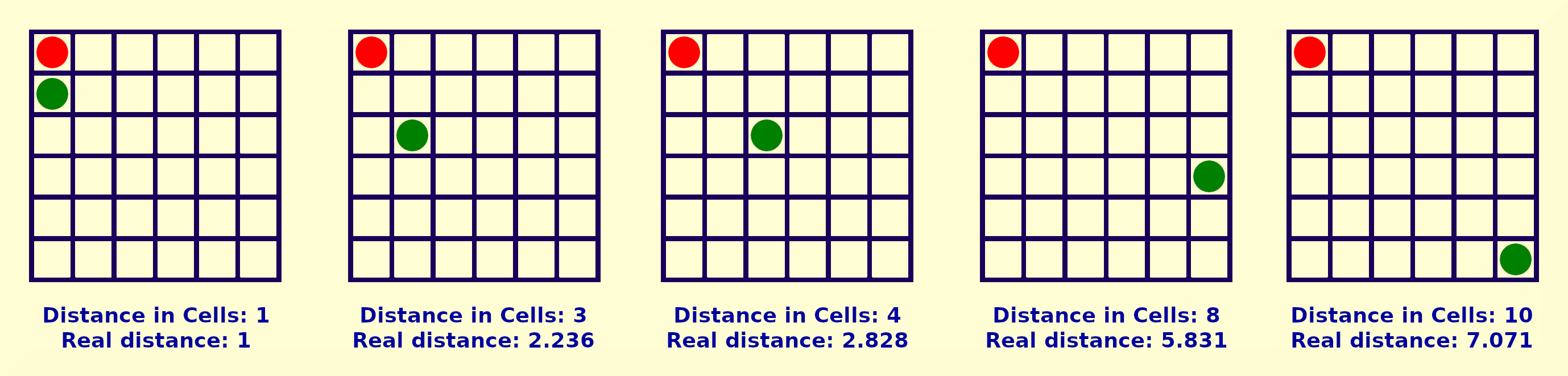
圖 6：測量兩點之間距離的不同標準

圖形結果
C語言程序直接在視頻上顯示人的位置地圖。這種可視化是在終端上進行的；因此，圖形方面不是非常令人愉快。然而，該程序提供了一個數據導出功能，允許將信息和點的坐標導出到文本文件，并允許作為腳本直接導入 Octave 數學環境。這樣，從圖形的角度來看，地圖與人的可視化更加令人愉快和有吸引力。正是當程序找到一個新的解決方案時，除了在監視器上顯示結果之外，它還將它們作為 Octave 的腳本保存到一個文本文件 (distance.m) 中，其中包含繪制圖形地圖的有用信息（圖 7）。這樣，顯示的地圖將與文本地圖相同，但具有更加美觀和優雅的圖形外觀。

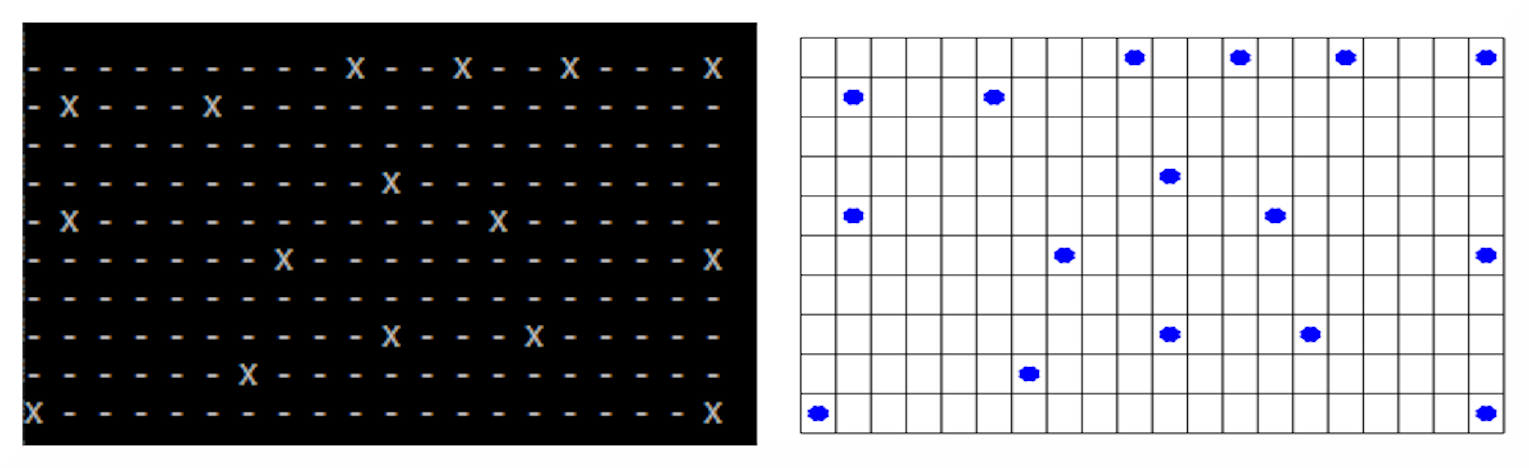
圖 7：文字地圖和圖形地圖是等價的。

下面，我們可以看到一個 Octave 腳本的示例：

堅持，稍等;

情節（19、9、'b*'、'線寬'、11）；

情節（15、9、'b*'、'線寬'、11）；

情節（12、9、'b*'、'線寬'、11）；

情節（ 9 ， 9 ， 'b*' ， '線寬' ， 11）；

線（[-0.5,19.500000]，[-0.500000，-0.500000]，'顏色'，'k'）；

線（[-0.5,19.500000]，[0.500000,0.500000]，'顏色'，'k'）；

線（[-0.5,19.500000]，[1.500000,1.500000]，'顏色'，'k'）；

線（[-0.5,19.500000]，[2.500000,2.500000]，'顏色'，'k'）；

線（[18.500000,18.500000]，[-0.5,9.500000]，'顏色'，'k'）；

線（[19.500000,19.500000]，[-0.5,9.500000]，'顏色'，'k'）；

暫緩；

非常大的數字！

人在網格上的定位相當于組合計算的“簡單組合”的計算。簡單組合的數量如圖 8所示。以下是一些顯著結果的例子：

6行×6列×6人：1,947,792種組合

20行×10列×16人：169,152,626,591,028,520,278,300種組合

50行×20列×40人：555,974,423,571,664,033,815,804,589,243,553,849,851,258,056,649,719,919,687,842,027,223,208,475種組合

我們可以立即理解，對于這些非常高的數字，蠻力方法是無法解決的。

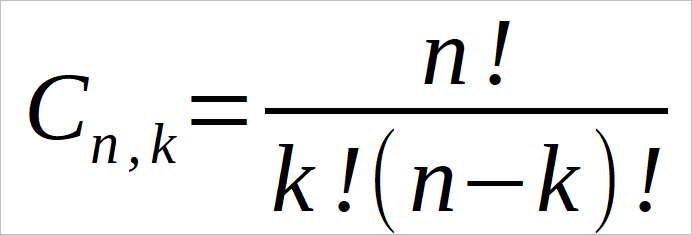
圖 8：簡單組合的公式

結論
本文介紹的研究方法不是最好的，也無法找到最好的結果。獲得的組合可用于對本文主題中提出的問題進行一般估計。蒙特卡洛方法有很多限制，例如它的相對緩慢。否則不可能，因為程序可以生成的數據和信息數量非常多（數十億個組合），沒有計算機或人類能夠計算出這樣的數字。對于相對較少的信息，達到最終解決方案很簡單。但是如果對象的數量或網格的尺寸增加，計算時間將成倍增長。增加搜索參數很不方便。該程序采用的方法也被定義為“蠻力”。計算上，這是一項非常繁重的工作，不能確定最終結果，并且可能會多次重復相同的解決方案。但是這種方法對于所有那些運行參數和因變量非常多的研究應用來說確實很有用。有時，尋找可能的解決方案可能會持續一整夜，尤其是在網格非常大且人數眾多的情況下。搜索時間還取決于計算機的速度和使用的編譯器類型。本文中進行的實驗可以為程序員創建更復雜和更復雜的程序提供新的思路。它代表了未來功能發展的起點。該程序的一個有趣的實現也可以包含人工智能。為這個非常復雜的目的確定最終解決方案可能很有用。本文所附的操作代碼是用 C 語言編寫的，可以很容易地翻譯成任何其他編程語言。程序注釋足夠，任何程序員也可以找到其他點來修改和改進它。除了提供教學實用程序之外，本文中采用的過程在代碼編寫和使用方面都非常有趣。該系統是完全自主的，因為程序提供的結果是不可預測的，因為數據和信息是隨機處理的。任何程序員也可以找到其他點來修改和改進它。除了提供教學實用程序之外，本文中采用的過程在代碼編寫和使用方面都非常有趣。該系統是完全自主的，因為程序提供的結果是不可預測的，因為數據和信息是隨機處理的。任何程序員也可以找到其他點來修改和改進它。除了提供教學實用程序之外，本文中采用的過程在代碼編寫和使用方面都非常有趣。該系統是完全自主的，因為程序提供的結果是不可預測的，因為數據和信息是隨機處理的。

審核編輯 黃昊宇