卡爾曼濾波(Kalman filtering)一種利用線性系統(tǒng)狀態(tài)方程,通過系統(tǒng)輸入輸出觀測數(shù)據(jù),對系統(tǒng)狀態(tài)進(jìn)行最優(yōu)估計的算法。由于觀測數(shù)據(jù)中包括系統(tǒng)中的噪聲和干擾的影響,所以最優(yōu)估計也可看作是濾波過程。
斯坦利·施密特(Stanley Schmidt)首次實(shí)現(xiàn)了卡爾曼濾波器。卡爾曼在NASA埃姆斯研究中心訪問時,發(fā)現(xiàn)他的方法對于解決阿波羅計劃的軌道預(yù)測很有用,后來阿波羅飛船的導(dǎo)航電腦使用了這種濾波器。 關(guān)于這種濾波器的論文由Swerling (1958), Kalman (1960)與 Kalman and Bucy (1961)發(fā)表。
數(shù)據(jù)濾波是去除噪聲還原真實(shí)數(shù)據(jù)的一種數(shù)據(jù)處理技術(shù), Kalman濾波在測量方差已知的情況下能夠從一系列存在測量噪聲的數(shù)據(jù)中,估計動態(tài)系統(tǒng)的狀態(tài)。 由于, 它便于計算機(jī)編程實(shí)現(xiàn), 并能夠?qū)ΜF(xiàn)場采集的數(shù)據(jù)進(jìn)行實(shí)時的更新和處理, Kalman濾波是目前應(yīng)用最為廣泛的濾波方法, 在通信, 導(dǎo)航, 制導(dǎo)與控制等多領(lǐng)域得到了較好的應(yīng)用。
性質(zhì)
①卡爾曼濾波是一個算法,它適用于線性、離散和有限維系統(tǒng)。每一個有外部變量的自回歸移動平均系統(tǒng)(ARMAX)或可用有理傳遞函數(shù)表示的系統(tǒng)都可以轉(zhuǎn)換成用狀態(tài)空間表示的系統(tǒng),從而能用卡爾曼濾波進(jìn)行計算。
②任何一組觀測數(shù)據(jù)都無助于消除x(t)的確定性。增益K(t)也同樣地與觀測數(shù)據(jù)無關(guān)。
③當(dāng)觀測數(shù)據(jù)和狀態(tài)聯(lián)合服從高斯分布時用卡爾曼遞歸公式計算得到的是高斯隨機(jī)變量的條件均值和條件方差,從而卡爾曼濾波公式給出了計算狀態(tài)的條件概率密度的更新過程線性最小方差估計,也就是最小方差估計。
卡爾曼濾波理解及代碼分析
鑒于網(wǎng)上的代碼以及分析的各種錯誤,所以寫一個正確的詳細(xì)的分析。
過程方程以及量測方程
X(K)=AX(K-1)+BU(K-1)+W(K-1)
Z(K)=HX(K)+V(K)
說明,下面帶T的表示轉(zhuǎn)置。
卡爾曼濾波的黃金五條公式
X(k|k-1)=AX(k-1|k-1)+BU(k)………。先驗(yàn)估計
P(k|k-1)=A P(k-1| k-1) AT+Q………。誤差協(xié)方差
Kg(k)= P(k|k-1) HT / (H P(k|k-1) HT + R)………。計算卡爾曼增益
X(k|k)= X(k|k-1) + Kg(k)(Z(k) - H X(k|k-1))………。修正估計
P(k|k)=( I-Kg(k) H) P(k|k-1)………。更新誤差協(xié)方差
下面的程序主要針對MPU6050的姿態(tài)角的濾波。
float Q_angle=0.001; //陀螺儀噪聲的協(xié)方差
float Q_gyro=0.003; //陀螺儀漂移噪聲的協(xié)方差
float R_angle=0.5; // 加速度計的協(xié)方差
float dt=0.005;
char C_0 = 1;
float Q_bias=0, Angle_err=0; //Q_bias為陀螺儀漂移
float PCt_0=0, PCt_1=0, E=0;
float K_0=0, K_1=0, t_0=0, t_1=0;
float Pdot[4] ={0,0,0,0};
float PP[2][2] = { { 1, 0 },{ 0, 1 } };12345678910
首先建立的是過程方程,這里的狀態(tài)變量是angle以及Q_bias,角度以及陀螺儀的漂移。
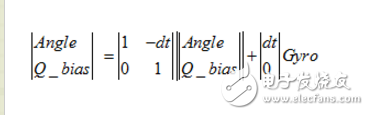
那么已經(jīng)建立了這里的預(yù)測方程,沒有加上噪聲。
void Kalman_Filter(float Gyro,float Accel)
{ //Gyro陀螺儀的測量值,Accel加速度計的角度計算值
Angle+=(Gyro - Q_bias) * dt;
//角度測量模型方程
//就漂移來說認(rèn)為每次都是相同的Q_bias=Q_bias;
//由此得到矩陣1234567
上面的代碼就對應(yīng)著預(yù)測方程。對應(yīng)著卡爾曼濾波的五個公式的第一條:X(k|k-1)=AX(k-1|k-1)+BU(k)
這里再分析第二條公式,P(k|k-1)=A P(k-1| k-1) AT+Q。可以在之前看出,A=[1,-dt;0,1]。而Q的定義如下:
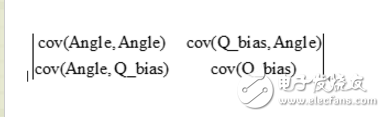
因?yàn)榻嵌仍肼暫屯勇輧x的角速度的漂移噪聲相互獨(dú)立,所以為一個對角矩陣。然后,Q_angle,Q_gyro再程序開頭已經(jīng)給出。所以設(shè)P=[a,b;c,d]
的出一個更新的式子,
[acbd]=[10?dt1][acbd][1?dt01]+[Qangle00Qgyro]
最后的到的更新的方法
[acbd]=[a?c?dt?b?dt+d?dt?dtc?d?dtb?d?dtd]+[Qangle00Qgyro]
所以看代碼,可以看出寫的極為的不合理,但是都是這樣寫的,先看一看。
Pdot[0]=Q_angle - PP[0][1] - PP[1][0];
Pdot[1] = -PP[1][1];
Pdot[2] = -PP[1][1];
Pdot[3] = Q_gyro;
PP[0][0] += Pdot[0] * dt;
PP[0][1] += Pdot[1] * dt;
PP[1][0] += Pdot[2] * dt;
PP[1][1] += Pdot[3] * dt;123456789
對照上面的公式,還是可以看出來,PP就是[a,b;c,d]的,但是注意,Pdot只是矩陣運(yùn)算的中間值,但是不知為什么要叫成Pdot,誤人子弟。而且最大的錯誤在于這樣寫,Q乘以了一個dt,但是最后并不會怎么影響,因?yàn)镼也是初始給的一個值而已,但是這樣寫還是有問題的,還是按照推導(dǎo)來寫比較好。
再是第三個公式來計算卡爾曼增益,Kg(k)= P(k|k-1) HT / (H P(k|k-1) HT + R),所以這里要做的就是再建立一個量測方程,這里測量的值是加速度計算出來的角度值,所以
Accelangle=[10][angleQbias]+R
所以H=[1 0],卡爾曼增益就是一個二維向量[k0,k1]T。
直接帶入計算第三個公式。
PCt_0 = C_0 * PP[0][0];//矩陣乘法的中間變量
PCt_1 = C_0 * PP[1][0];//C_0=1
//分母
E = R_angle + C_0 * PCt_0;
//增益值
K_0 = PCt_0 / E;
K_1 = PCt_1 / E; 1234567
基本還算比較清楚,但是命名的話真的不忍心吐槽。
再看第四個公式,X(k|k)= X(k|k-1) + Kg(k)(Z(k) - H X(k|k-1))。
Angle_err = Accel - Angle; //Accel是加速度計的值,算出來的角度的測量值。
Angle += K_0 * Angle_err; //對狀態(tài)的卡爾曼估計。
Q_bias += K_1 * Angle_err;
Gyro_x = Gyro - Q_bias; //計算得角速度值,這里由于每次對Q_bias更新,就更準(zhǔn)確,比初始矯正后不管肯定要好很多。123456
第五個公式對PP進(jìn)行更新,P(k|k)=( I-Kg(k) H) P(k|k-1);
t_0 = PCt_0; //矩陣計算中間變量
t_1 = C_0 * PP[0][1];
PP[0][0] -= K_0 * t_0;
PP[0][1] -= K_0 * t_1;
PP[1][0] -= K_1 * t_0;
PP[1][1] -= K_1 * t_1;
}12345678
已經(jīng)不忍心吐槽他的命名了。到這里基本分析完畢,至于卡爾曼濾波的證明推導(dǎo),可以參考其他,這里只是分析代碼,但是網(wǎng)上基本都是這樣寫的,有分析的,但是要么就是直接甩代碼,要么就是分析的很多錯誤,太亂,決定寫一個完整的正確的分析mpu6050卡爾曼濾波的程序。
 電子發(fā)燒友App
電子發(fā)燒友App





















評論