本期講分?jǐn)?shù)槽繞組的對(duì)稱條件和并聯(lián)支路數(shù)。
1 分?jǐn)?shù)槽繞組的對(duì)稱條件
對(duì)于整數(shù)槽繞組,由于每極每相槽數(shù)為整數(shù),每極每相的槽數(shù)相等,總是能夠構(gòu)成對(duì)稱的多相繞組,不存在繞組不對(duì)稱的問題。但對(duì)于分?jǐn)?shù)槽繞組,由于每個(gè)相帶的槽數(shù)不相等,如果極槽配合不當(dāng),可能無法構(gòu)成對(duì)稱的多相繞組,極槽配合必須要滿足一定的條件才能構(gòu)成對(duì)稱的多相繞組。
關(guān)于分?jǐn)?shù)槽繞組的對(duì)稱條件,有許多表達(dá)形式,不同文獻(xiàn)上講的對(duì)稱條件也不同,但都是從不同角度推導(dǎo)出來的結(jié)果,表達(dá)方式不同而已,其本質(zhì)是等效的,滿足一種形式的對(duì)稱條件,其它也必然滿足。接下來我們就介紹幾種不同形式的分?jǐn)?shù)槽繞組對(duì)稱條件。
構(gòu)成對(duì)稱多相繞組的條件有兩個(gè):第一個(gè)對(duì)稱條件就是每相繞組的線圈個(gè)數(shù)必須相等;第二個(gè)對(duì)稱條件是各相繞組在定子圓周上的分布必須均勻,即相鄰兩相繞組的軸線夾角相等,每相繞組產(chǎn)生的電勢(shì)和磁勢(shì)要對(duì)稱。兩個(gè)條件必須同時(shí)滿足才能構(gòu)成對(duì)稱多相繞組。下面我們分別講解這兩個(gè)對(duì)稱條件。
1.1 第一個(gè)對(duì)稱條件
如上所述,構(gòu)成對(duì)稱多相繞組的第一個(gè)條件是每相繞組的線圈個(gè)數(shù)必須相等,這個(gè)條件應(yīng)該很好理解,如果每相繞組的線圈不相等,那么就談不上對(duì)稱。設(shè)定子槽數(shù)為Z1,相數(shù)為m,極對(duì)數(shù)為p,每極每相槽數(shù)為q,則對(duì)于單層繞組來說,定子Z1個(gè)槽就一共有Z1/2個(gè)線圈,要想每相繞組線圈個(gè)數(shù)相等,這Z1/2個(gè)線圈就必須能夠被相數(shù)m整除,即對(duì)于單層繞組,第一個(gè)對(duì)稱條件為:
Z1/(2m)=pq=整數(shù)?(1)
對(duì)于雙層繞組,Z1個(gè)槽一共就有Z1個(gè)線圈,要想每相繞組線圈個(gè)數(shù)相等,這Z1個(gè)線圈就必須能夠被相數(shù)m整除,即對(duì)于雙層繞組,第一個(gè)對(duì)稱條件為:
Z1/m=2pq=整數(shù)?(2)
由⑴、⑵式可見,整數(shù)槽繞組總是可以滿足第一對(duì)稱條件的,因?yàn)檎麛?shù)槽繞組的p和q都是整數(shù),二者相乘當(dāng)然還是整數(shù)。
對(duì)于分?jǐn)?shù)槽繞組,由于q=N/d為一個(gè)不可約的分?jǐn)?shù),對(duì)單層分?jǐn)?shù)槽繞組,第一個(gè)對(duì)稱條件:Z1/(2m)=pq=p?(N/d)=整數(shù),由于N與d不能整除,要想滿足該條件,必須p與d能夠整除,即對(duì)于分?jǐn)?shù)槽單層繞組,第一個(gè)對(duì)稱條件可演化為:
p/d=整數(shù)???? ???????????????????????????????(3)
同理對(duì)于雙層分?jǐn)?shù)槽繞組的第一個(gè)對(duì)稱條件可演化為:
2p/d=整數(shù)???? ???????????????????????????????(4)
比較⑶、⑷式可見,雙層繞組比單層繞組更容易滿足第一個(gè)對(duì)稱條件,在設(shè)計(jì)時(shí)雙層繞組具有更多的極槽配合選擇余地。
1.2 第二個(gè)對(duì)稱條件
第二個(gè)對(duì)稱條件是每相繞組的布置要對(duì)稱,各相繞組產(chǎn)生的電勢(shì)和磁勢(shì)分布要對(duì)稱。這個(gè)條件進(jìn)一步推論一下就是各相電勢(shì)之間的相位差均勻,或每相繞組的相帶寬度要相等。可以從不同的角度入手來推導(dǎo)出第二個(gè)對(duì)稱條件。
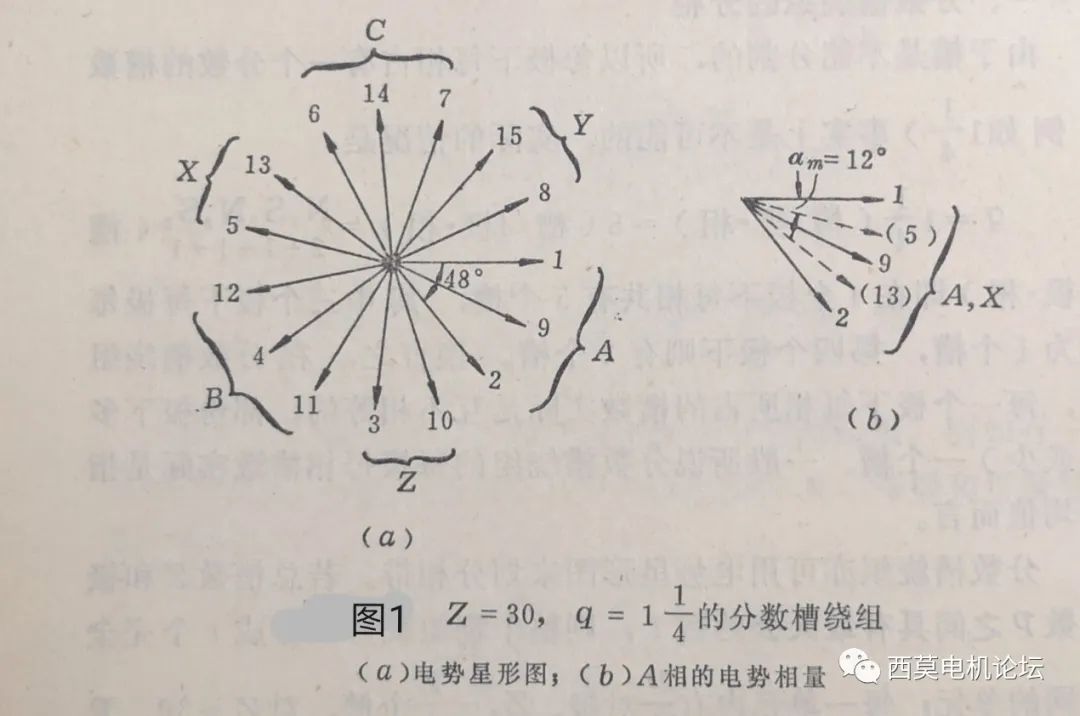
1.2.1 從槽電勢(shì)星型圖推導(dǎo)第二個(gè)對(duì)稱條件
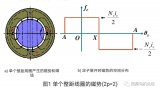
槽電勢(shì)星型圖反映了各槽電勢(shì)或者說各線圈電勢(shì)的相位關(guān)系,每個(gè)單元電機(jī)對(duì)應(yīng)一個(gè)槽電勢(shì)星型圖,各單元電機(jī)的槽電勢(shì)星型圖是重疊,我們把一個(gè)單元電機(jī)對(duì)應(yīng)的槽電勢(shì)星型圖稱為基本星型圖,由于各單元電機(jī)的槽電勢(shì)星型圖是重疊的,因此只要研究一個(gè)單元的槽電勢(shì)星型圖,其它單元電機(jī)即可簡(jiǎn)單復(fù)制。一個(gè)基本星型圖里包含許多個(gè)槽電勢(shì)相量,要想使多相繞組對(duì)稱,必須要把基本星型圖上的相量個(gè)數(shù)能夠平均分配給每一相,也就是說,基本星型圖中的相量個(gè)數(shù)必須能夠被相數(shù)整除。基于此即可推出構(gòu)成對(duì)稱多相繞組的第二個(gè)條件為:
Z′=Z0/m=(Z1/t)/m=Z1/(m?t)=整數(shù)?(5)
式中:Z′為每個(gè)單元電機(jī)每相分得的槽數(shù),或者說一個(gè)基本星型圖內(nèi)每相包括的相量個(gè)數(shù);Z0為單元電機(jī)的槽數(shù),或者叫基本星型圖中的相量總個(gè)數(shù);m為相數(shù);Z1為定子總槽數(shù);t為單元電機(jī)個(gè)數(shù),即Z1與極對(duì)數(shù)p的最大公約數(shù)。
顯然對(duì)于整數(shù)槽繞組,由于t=p,⑸式永遠(yuǎn)是滿足的,因此整數(shù)槽繞組總是能夠構(gòu)成對(duì)稱多相繞組。
對(duì)于分?jǐn)?shù)槽繞組,需要根據(jù)給出的電機(jī)總槽數(shù)Z1,極對(duì)數(shù)p,相數(shù)m,分兩步判斷是否能夠構(gòu)成對(duì)稱繞組:第一步,首先求出總槽數(shù)Z1與極對(duì)數(shù)p的最大公約數(shù)t;第二步,根據(jù)⑸式計(jì)算Z1/(m?t)看是否能夠整除,如果能夠整除就可以構(gòu)成對(duì)稱多相繞組,否則不能構(gòu)成對(duì)稱多相繞組。
1.2.2 從相帶寬度推導(dǎo)第二個(gè)對(duì)稱條件
一個(gè)基本星型圖中的相量個(gè)數(shù)為Z0=Z1/t,則相鄰兩個(gè)相量之間的相位差(即相距角):
α′=360o/Z0=360?t/Z1? (6)
對(duì)于m相對(duì)稱繞組,每相的相帶寬度為:
αφ=360o/m ??????????????????????????????(7)
要想構(gòu)成m相對(duì)稱繞組,則一個(gè)相帶內(nèi)必須包括整數(shù)個(gè)槽電勢(shì)相量,即相帶寬度αφ必須要能被相距角α′整除,即:
αφ/α′=(360o/m)/(360?t/Z1)=Z1/(m?t)=整數(shù)?(8)
式⑻即為從相帶劃分的角度推導(dǎo)出的對(duì)稱條件,比較⑻式和⑸式可見,兩式是一樣的。只不過是從不同的角度入手,推導(dǎo)出了同樣的結(jié)果。
1.2.3 用每極每相槽數(shù)q來判斷對(duì)稱條件
以上從兩個(gè)不同角度入手,推導(dǎo)出了同樣的構(gòu)成多相繞組的對(duì)稱條件,即:
Z1/(m?t)=整數(shù)?(9)
用這個(gè)對(duì)稱條件來判斷一個(gè)分?jǐn)?shù)槽的極槽配合能否構(gòu)成多相對(duì)稱繞組固然是可以的,但判斷時(shí)需要分兩步,先求出Z1與p的最大公約數(shù)t,再用⑼式判斷是否能夠構(gòu)成對(duì)稱繞組,這樣不僅比較麻煩,而且也不易記憶。實(shí)踐中常用另外一種簡(jiǎn)單的判別方法,即用每極每相槽數(shù)q的分母d來判斷是否能夠構(gòu)成多相對(duì)稱繞組。這里先把結(jié)果告訴大家,這個(gè)判別方法就是:看每極每相槽數(shù)q的分母d是否能被相數(shù)m整除,如果能夠整除就不能構(gòu)成多相對(duì)稱繞組;如果不能整除就能夠構(gòu)成多相對(duì)稱繞組。即構(gòu)成多相對(duì)稱分?jǐn)?shù)槽繞組的條件為:
d/m≠整數(shù)???? ??????????????????????????????(10)
對(duì)于三相繞組,就是d不能被3整除。其實(shí)(10)式也是從(9)式推導(dǎo)而來的,二者是等效的。接下來就用兩種方法來證明這個(gè)對(duì)稱條件。
【證法Ⅰ】設(shè)每極每相槽數(shù):
q=b+c/d=(bd+c)/d
則:
Z′=Z1/(m?t)=2p?m?q/(m?t)=(2p/t)?q=(2p/t)?(bd+c)/d=整數(shù)?(11)
由于(bd+c)/d是除不盡的分?jǐn)?shù),要想滿足(11)式,只有2p/t能夠被d整除。又由于t是Z1與p的最大公約數(shù),所以Z1=m?t?Z′與p=(p/t)?t之間除了最大公約數(shù)t之外,p/t與m之間不能再有不是1的公約數(shù),另外由于多相電機(jī)m>2,所以2p/t也不能被m整除。綜上,要想滿足(11)式,必須2(p/t)能被d整除,而2(p/t)不能被m整除,所以d也不能被m整除。
【證法Ⅱ】設(shè)每極每相槽數(shù):
q=b+c/d=(bd+c)/d=N/d (12)
則:
Z1=2mpq=2mpN/d (13)
p=d?(p/d) ??????????????????(14)
由第一個(gè)對(duì)稱條件⑶式可知,p/d=整數(shù),根據(jù)(13)、(14)式,這個(gè)整數(shù)p/d顯然是Z1與p的一個(gè)公約數(shù),又由于N和d不可約,Z1和p的其它公約數(shù)只能包含于2m和d中,換句話說,Z1和p的其它公約數(shù)必定也是2m和d的公約數(shù),設(shè)這些其它公約數(shù)為k,則Z1和p的最大公約數(shù)(單元電機(jī)個(gè)數(shù))即為:
t=k?(p/d) ????????????????????????????(15)
將(13)、(15)式代入⑼式中,得第二個(gè)對(duì)稱條件為:
Z1/(mt)=(2mpN/d)/(mkp/d)=2N/k=整數(shù)?(16)
由于d的約數(shù)k不能是N的約數(shù),因此k只能是1或2。也就是說在2m和d中只可能有1和2兩個(gè)公約數(shù),無論是1還是2,對(duì)多相電機(jī)(m>2),d和m都不會(huì)有大于2的公約數(shù),即第二個(gè)對(duì)稱條件為:
d/m≠整數(shù)???? ????????????????????????????(17)
對(duì)于三相電機(jī):
d/3≠整數(shù)?????????????????????????????????(18)
以上用兩種方法證明了構(gòu)成對(duì)稱多相繞組的條件。再次將兩個(gè)對(duì)稱條件重復(fù)如下:
對(duì)單層分?jǐn)?shù)槽繞組:
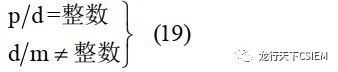
? 對(duì)于雙層分?jǐn)?shù)槽繞組:
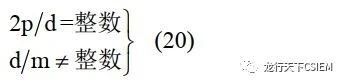
? 由以上兩式可見,對(duì)于三相(m=3)分?jǐn)?shù)槽電機(jī),如果極對(duì)數(shù)為3的倍數(shù)次方(p=3、9、27…),則絕對(duì)不能滿足式(19)的條件,因此這種極對(duì)數(shù)的分?jǐn)?shù)槽電機(jī)是絕對(duì)不能構(gòu)成單層三相分?jǐn)?shù)槽繞組的。
2 分?jǐn)?shù)槽繞組的并聯(lián)支路數(shù)
能夠構(gòu)成并聯(lián)支路的條件是支路中包含的線圈電勢(shì)疊加后的大小和相位都相同才能被并聯(lián)起來。對(duì)于分?jǐn)?shù)槽繞組分兩種情況,第一種情況:如果一個(gè)單元電機(jī)中每相槽數(shù)是奇數(shù),則不能等分成兩個(gè)相等的正負(fù)相帶,這種情況下只能構(gòu)成雙層繞組,且一個(gè)單元電機(jī)只能構(gòu)成一條并聯(lián)支路,t個(gè)單元電機(jī)最多可以構(gòu)成t條并聯(lián)支路。第二種情況:如果一個(gè)單元電機(jī)中每相槽數(shù)是偶數(shù),則可以等分成兩個(gè)相等的正負(fù)相帶,這種情況下對(duì)于雙層繞組,一個(gè)單元電機(jī)中可以構(gòu)成兩條并聯(lián)支路,t個(gè)單元電機(jī)最多可以構(gòu)成2t條并聯(lián)支路;這種情況也可以構(gòu)成單層繞組,一個(gè)單元只能構(gòu)成一條并聯(lián)支路,t個(gè)單元電機(jī)最多可以構(gòu)成t條并聯(lián)支路(后面會(huì)提到有特例)。接下來我們就分這兩種情況,分別介紹分?jǐn)?shù)槽繞組的并聯(lián)支路數(shù)。
2.1 當(dāng)Z′為奇數(shù)時(shí)的最大并聯(lián)支路數(shù)
分?jǐn)?shù)槽繞組一個(gè)單元電機(jī)中每相的槽數(shù)為Z′=Z1/t?m。
則每極每相槽數(shù):
q=Z1/(2pm)=Z′?t?m/(2pm)=Z′/(2p/t)=Z′/(2p′)=N/d (21)
其中:Z′=Z0/m;Z0=Z1/t為每個(gè)單元電機(jī)的槽數(shù);p′=p/t為每個(gè)單元電機(jī)的極對(duì)數(shù)。由于t為Z1與p的最大公約數(shù),故Z0和p′不可約,因此Z′與p′也不可約,又由于Z′為奇數(shù),故Z′與2也不可約,因此Z′與2p′必不可約,即Z′/2p′為最簡(jiǎn)分?jǐn)?shù),那必然是N=Z′;d=2p′=2p/t。由此可見,單元電機(jī)個(gè)數(shù)為:
t=2p/d ???????????????????????????????(22)
Z′為奇數(shù),即一個(gè)單元電機(jī)中每相槽數(shù)為奇數(shù),不能等分成兩個(gè)相等的正負(fù)相帶,因此這種情況只能構(gòu)成雙層繞組,且一個(gè)單元電機(jī)只能一條并聯(lián)支路,t個(gè)單元電機(jī)最多可以構(gòu)成t條并聯(lián)支路。即這種情況的最大并聯(lián)支路數(shù)為:
amax=t=2p/d ????????????????????????????(23)
由于用Z′的奇偶作為判別條件需要復(fù)雜的計(jì)算,不太簡(jiǎn)便和直觀,分?jǐn)?shù)槽繞組通常都是先算出每極每相槽數(shù)q,這樣其分母d自然就知道奇偶,因此實(shí)踐中常用d的奇偶作為判別條件。由式(21)可見,當(dāng)一個(gè)單元電機(jī)中每相的槽數(shù)Z′=N為奇數(shù)時(shí),d=2p/t必為偶數(shù),因此上述Z′為奇數(shù)的前提條件可以轉(zhuǎn)化為d為偶數(shù)。
小結(jié)一下:當(dāng)d為偶數(shù)時(shí),只能構(gòu)成雙層分?jǐn)?shù)槽繞組,其最大并聯(lián)支路數(shù)為2p/d。
2.2 當(dāng)Z′為偶數(shù)時(shí)的最大并聯(lián)支路數(shù)
如果Z′為偶數(shù),則每極每相槽數(shù):
q=Z1/(2pm)=Z′?t?m/(2pm)=(Z′/2)/(p/t)=(Z′/2)/p′=N/d (24)
同理,由于Z′與p′不可約,Z′/2與p′必不可約,即(Z′/2)/p′為最簡(jiǎn)分?jǐn)?shù),那必然是N=Z′/2;d=p′=p/t,則單元電機(jī)個(gè)數(shù)為:
t=p/d ??????????????????????????????????(25)
另外由于Z′與p′不可約,Z′為偶數(shù)時(shí),p′必為奇數(shù),因此也可以把Z′為偶數(shù)的前提條件轉(zhuǎn)化為d為奇數(shù)。即d為奇數(shù)時(shí),可以把每相等分成兩個(gè)相等的正負(fù)相帶,此時(shí)即可以構(gòu)成雙層繞組,也可以構(gòu)成單層繞組。
如果是雙層繞組,一個(gè)單元電機(jī)可以構(gòu)成兩條并聯(lián)支路,t個(gè)單元電機(jī)最多可以構(gòu)成2t條并聯(lián)支路,即這種情況對(duì)雙層繞組最大并聯(lián)支路數(shù)為:
amax=2t=2p/d ????????????????????????????(26)
如果是單層繞組,一個(gè)單元只能構(gòu)成一條并聯(lián)支路,t個(gè)單元電機(jī)最多可以構(gòu)成t條并聯(lián)支路,即這種情況對(duì)單層繞組最大并聯(lián)支路數(shù)為:
amax=t=p/d ?????????????????????????????(27)
另外,這種情況還存在一種特例,就是如果Z′能夠被4整除,也就是N為偶數(shù)時(shí),則一個(gè)單元電機(jī)內(nèi)仍然可以將每個(gè)正相帶和負(fù)相帶的槽數(shù)再平分成兩份,兩份槽內(nèi)導(dǎo)體在端部分別向兩邊跨接構(gòu)成單層繞組的兩條并聯(lián)支路,t個(gè)單元電機(jī),就能夠構(gòu)成最大并聯(lián)支路數(shù)為2t的單層繞組,即此時(shí)最大并聯(lián)支路數(shù)為:
amax=2t=2p/d ????????????????????????????(28)
這種特例情況類似q為偶數(shù)的整數(shù)槽繞組,采用鏈?zhǔn)浇臃〞r(shí)仍然可以構(gòu)成最大并聯(lián)支路數(shù)為2p的單層繞組,有關(guān)詳細(xì)論述參見《電機(jī)繞組(2)》中的示例二和示例三,這里不再贅述。
小結(jié)一下:當(dāng)d為奇數(shù)時(shí),即可以構(gòu)成雙層分?jǐn)?shù)槽繞組,也可以構(gòu)成單層分?jǐn)?shù)槽繞組。構(gòu)成雙層繞組時(shí),其最大并聯(lián)支路數(shù)為2p/d;構(gòu)成單層繞組時(shí),如果N為奇數(shù)則最大并聯(lián)支路數(shù)為p/d;如果N為偶數(shù),則最大并聯(lián)支路數(shù)為2p/d。
2.3 分?jǐn)?shù)槽繞組最大并聯(lián)支路數(shù)總結(jié)
綜上所述,由式(23)、(26)、(27)、(28)可以得出以下結(jié)論:
【結(jié)論Ⅰ】無論d為偶數(shù)還是奇數(shù),都可以構(gòu)成雙層繞組,雙層分?jǐn)?shù)槽繞組的最大并聯(lián)支路數(shù)都是2p/d。
【結(jié)論Ⅱ】只有d為奇數(shù)時(shí),才可以構(gòu)成單層繞組。構(gòu)成單層繞組時(shí),如果N為偶數(shù),則最大并聯(lián)支路數(shù)仍為2p/d;如果N為奇數(shù)則最大并聯(lián)支路數(shù)為p/d。
2.4 分?jǐn)?shù)槽繞組的實(shí)際并聯(lián)支路數(shù)
以上論述的是分?jǐn)?shù)槽繞組可能構(gòu)成的最大并聯(lián)支路數(shù),實(shí)際電機(jī)中的并聯(lián)支路數(shù)a可以少于上述最大并聯(lián)支路數(shù)amax,但必須是最大并聯(lián)支路數(shù)的約數(shù),即:
amax/a=整數(shù)??? ?????????????????????????????(29)
上述介紹了分?jǐn)?shù)槽繞組的對(duì)稱條件和并聯(lián)支路數(shù),以上分析可見,雖然就這么幾個(gè)數(shù)字倒騰過來倒騰過去,用的都是些小學(xué)數(shù)學(xué)知識(shí),但消化起來還是很燒腦子的,想深入消化理解的同學(xué)們一定要靜下心來,多看幾遍慢慢理解,不想燒腦子的同學(xué)們看不懂也沒關(guān)系,你就記住文中的那些結(jié)論和結(jié)論性的判別式即可快速判斷極槽配合能否構(gòu)成對(duì)稱分?jǐn)?shù)槽繞組,能夠構(gòu)成幾路并聯(lián)。
編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App


























評(píng)論