貝葉斯定理提供了一種由P(c),P(x)和P(x | c)計算概率P(c | x)的方法。 看下面的等式:

?
其中:
P(c | x)是在x條件下c發生的概率。
P(c)是c發生的概率。
P(x | c)在c條件下x發生的概率。
P(x)是x發生的概率。
示例:
讓我們用一個例子來理解它。 下面我有一個天氣和相應的目標變量“玩游戲”的訓練數據集。 現在,我們需要根據天氣條件對玩家是否玩游戲進行分類。 我們按照以下步驟執行。
步驟1:將數據集轉換為頻率表
步驟2:通過發現像“Overcast”概率= 0.29和播放概率為0.64的概率來創建似然表。

?
步驟3:現在,使用樸素貝葉斯方程來計算每個類的概率。 其中概率最高的情況就是是預測的結果。
問題:
如果天氣晴朗,玩家會玩游戲,這個說法是正確的嗎?
我們可以使用上述方法解決,所以P(Yes | Sunny) = P( Sunny | Yes) * P(Yes) / P (Sunny)
這里,P(Sunny | Yes)= 3/9 = 0.33,P(Sunny)= 5/14 = 0.36,P(Yes)= 9/14 = 0.64
現在,P(Yes | Sunny)= 0.33 * 0.64 / 0.36 = 0.60,該事件發生的概率還是比較高的。
樸素貝葉斯使用類似的方法根據各種屬性預測不同分類的概率,該算法主要用于文本分類和具有多個類的問題。
Python Code
#Import Library
from sklearn.naive_bayes import GaussianNB
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create SVM classification object model = GaussianNB()
# there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)
R Code
library(e1071)
x <- cbind(x_train,y_train)
# Fitting model
fit <-naiveBayes(y_train ~ ., data = x)
summary(fit)
#Predict Output
predicted= predict(fit,x_test)
6. KNN (K-近鄰算法)
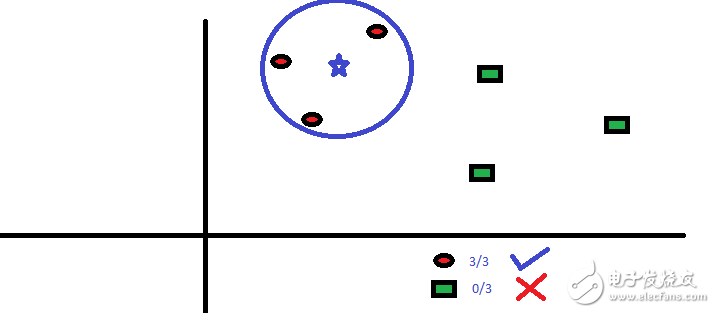
它可以用于分類和回歸問題, 然而,它在行業中被廣泛地應用于分類問題。 K-近鄰算法用于存儲所有訓練樣本集(所有已知的案列),并通過其k個鄰近數據多數投票對新的數據(或者案列)進行分類。通常,選擇k個最近鄰數據中出現次數最多的分類作為新數據的分類。
這些計算機的距離函數可以是歐幾里德,曼哈頓,閔可夫斯基和漢明距離。 前三個函數用于連續函數,第四個函數用于分類變量。 如果K = 1,則簡單地將該情況分配給其最近鄰的類。 有時,選擇K在執行KNN建模時是一個難點。
?
KNN可以輕松映射到我們的現實生活中。 如果你想了解一個人,你沒有任何信息,你可能想知道先去了解他的親密的朋友和他活動的圈子,從而獲得他/她的信息!
選擇KNN之前要考慮的事項:
KNN在計算上是昂貴的
變量應該被歸一化,否則更高的范圍變量可以偏移它
在進行KNN之前,預處理階段的工作更像去除離群值、噪聲值
Python Code
#Import Library
from sklearn.neighbors import KNeighborsClassifier
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create KNeighbors classifier object model
KNeighborsClassifier(n_neighbors=6) # default value for n_neighbors is 5
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)
R Code
library(knn)
x <- cbind(x_train,y_train)
# Fitting model
fit <-knn(y_train ~ ., data = x,k=5)
summary(fit)
#Predict Output
predicted= predict(fit,x_test)
7. K-Means
它是解決聚類問題的一種無監督算法。 其過程遵循一種簡單而簡單的方式,通過一定數量的聚類(假設k個聚類)對給定的數據集進行分類。 集群內的數據點與對等組是同構的和異構的。
嘗試從油墨印跡中找出形狀?(見下圖) k means 與這個活動相似, 你通過墨水漬形狀來判斷有多少群體存在!
?
下面兩點感覺原文解釋的不是很清楚,自己然后查了下國內的解釋方法
K-means如何形成集群
(1) 從 n個數據對象任意選擇 k 個對象作為初始聚類中心;
(2) 根據每個聚類對象的均值(中心對象),計算每個對象與這些中心對象的距離;并根據最小距離重新對相應對象進行劃分;
(3) 重新計算每個(有變化)聚類的均值(中心對象)
(4) 循環(2)到(3)直到每個聚類不再發生變化為止參考
 電子發燒友App
電子發燒友App

























評論