摘要:在以往的論文里,提到過薄膜電阻的阻值隨時間變化而發(fā)生漂移的現象,描述的是在“干熱”條件下發(fā)生的情況。然而,在相對濕度較高的地方或應用里使用電子設備時,對元器件的可靠性來說仍然是一個挑戰(zhàn)。因此,行業(yè)標準AEC-Q200要求在偏置濕度測試85℃ / 85 % RH條件下,也要對無源元件進行測試。通過認證的薄膜電阻采用了適當的穩(wěn)定R層和電絕緣漆,能夠通過 85 / 85測試。
會出現下面這些問題:
(1)通過1000小時的偏置85 / 85測試,對實際當中應用的薄膜電阻意味著什么?
(2) 在一定的負載和環(huán)境條件下,是否有可能通過使用經過一定時間之后的85 /85測試數據或HAST數據,預測在最壞情況下的電阻漂移?
要回答這些問題和其他與測試有關的問題,我們對電阻在40 °C / 93 % RH 和85 °C / 85 % RH的工作情況,以及常用的標準測試情況,進行了長時間的實驗對比。在大約0.5%和10%的最大標定工作功率下,使用我們最靈敏的薄膜電阻層系統(tǒng),將這些試驗的時間延長到4000小時。除此以外,我們還進行了70 °C / 90 % RH, 90 °C / 40 % RH, 以及HAST130條件下的測試,對電阻的溫度、濕度的線性度,以及電壓對漂移的影響進行了研究。
本文將說明這個對比研究的結果,那些數據點使我們能夠回答溫度和電壓的加速因子問題。這些成果將和現有的預測模型做對比。這些研究成果為設計出一個在整個溫度-濕度-時間域內覆蓋所有老化條件、系統(tǒng)特性和元器件健康預測的新模型提供了基礎,
主要內容
· 開發(fā)和定義一個電子元器件的通用(偏置)濕度加速和長期預測模型,并將這個模型用于研究靈敏的薄膜電阻。
· 模型考慮了熱和濕度對降級的影響,這樣就可以在整個溫度-濕度-時間域內做預測。
· 明確的ln√t – 1 / T框圖包含了全部信息,使我們能夠計算文中討論的塑模/漆,以及功能層上所有相關材料的數據(活化能,濕度有關的材料特性,偏置電壓加速效應等)。
· 老化/氧化和腐蝕之間是有區(qū)別的。通過將暴露時間標準化,替代被測參數的漂移,可以消除這些相互矛盾現象之間的不一致性。
· 通常用實際的當前蒸汽壓做為明確的物理速率,替換相對濕度rh。在我們的模型里,rh的作用是估計擴散的實際速率。
· 分別找出電絕緣漆或塑模的擴散特性,做為溫度和濕度影響元器件參數降級的主要因素。
1. 引言
在前一篇論文里已經介紹了在最高到175℃的相對溫度-時間-范圍內的干熱條件下如何預測漂移。主要發(fā)現是由阿倫尼烏斯定律推導出的隨時間變化的現象,以及過程常量Tstab。在時間相關的阿倫尼烏斯等式基礎上提出了預測模型,可以確保器件安全和可靠地工作,預計時間可以達到200000小時或 20年以上。
對于工作在非常重要且十分惡劣環(huán)境條件下的應用,汽車行業(yè)對可靠性提出了更高的目標。除了在很多年前就已成為標準的40 °C / 93 % RH測試,偏置85 °C / 85 % RH測試已經成為標準認證和車用無源元件的強制要求。尤其是無源元件的相互作用和降級機理的細節(jié)還相當模糊。在很多研討會和發(fā)布上,元器件制造商都表示85 / 85測試對他們的專用元器件來說太困難了(例如:AEC-RW 2012: Polymer-C; AEC-RW 2008: Tantalum-C,經過168小時的85 / 85測試)。
器件符合85 / 85對長期使用意味著什么(如17年的產品壽命,在標定電壓下可工作5000到7000小時),汽車行業(yè)對此是一頭霧水。因此對無源元件預測模型的問題和需求隨之而來,尤其是電阻。既然Lawson等式還是預測有源器件的主流方法,有人會問,Lawson預測模型是否也適合電阻的潮濕老化和降級呢。
很多開放式的問題促使我們去重拾我們已經研究過和公開出版的薄膜電阻的預測方法,到目前為止,這些問題還沒有合適的模型,能夠檢驗該怎么把偏置濕度現象考慮進來,或者做得更好一點,能夠整合進來。
2. 偏置濕度: 老化或腐蝕效應
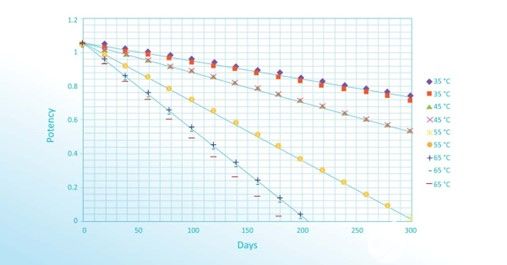
測試表明,由于熱尤其是潮濕條件的不同,過度潮濕測試的結果大相徑庭。在潮濕環(huán)境中暴露1000小時后,試驗結果的差異顯示在圖1中。
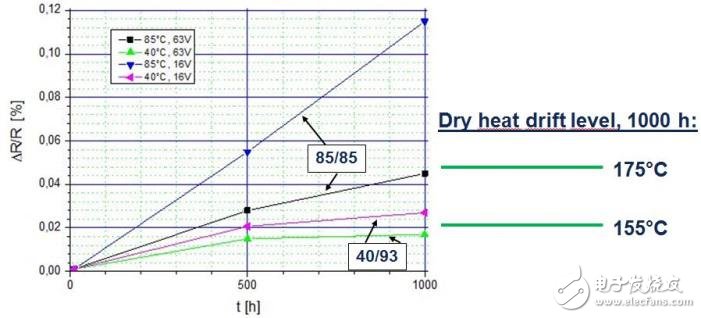
圖 1:試驗結果的差別
這些事實包含了很多開放式問題:
· 為什么測試溫度僅僅增加45K,偏置濕度的影響會這么大?
· 為什么薄膜電阻對偏置濕度的反應比干熱更敏感?
· 為什么更高的電壓會導致更低的漂移?
· 在偏置濕度測試中,降級的加速機制是什么?
· 是否有合適的方法,能夠估計和預測經過偏置濕度應力后的阻值漂移?
最初的85/85測試被設計成可以加速濕氣滲透進非密封的IC封裝,以便引發(fā)金屬層里的腐蝕失效。在評估測試結果的時候,應當始終搞清楚,測試結果是由(可預測)的老化過程還是由(破壞性)的降級造成的。這樣我們就可以徹底地區(qū)分氧化/鈍化效應和腐蝕機制。圖2顯示了由這兩種原因引起參數漂移的基本區(qū)別。
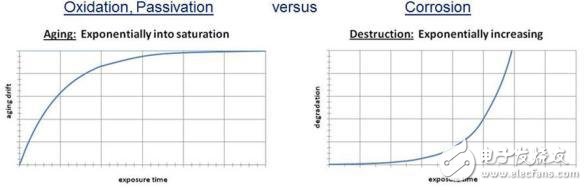
圖2: 氧化/鈍化與腐蝕機制
3. 深入研究的測試程序
我們的測試計劃通盤考慮了下面這些因素:
· 按照AEC-Q200(同一批次,對所有被測變體進行激光微調)的要求,使用認證過的靈敏的薄膜電阻阻值;
· 比較偏置濕度85 / 85 測試結果與40 / 93測試結果;
· 引入70℃ /90% RH和90℃ /40% RH這兩個中間測試狀態(tài);
· 延長測試或暴露時間到 4000小時 (10000小時);
· 使用兩種不同的電絕緣漆;
· 在每個變體上施加兩種電壓/負載(從額定電壓的10%到30%,利用偏置濕度測試,按照標準車用元器件的要求進行認證);
· 比較偏置測試和HAST 130(高加速應力測試:130℃和85%RH偏置濕度測試,相同的批次和電氣狀態(tài))的結果。
很重要的一點是,兩種漆都按照85 / 85(也就是說我們只按照行業(yè)標準對可用的樣品進行了基本的研究)的行業(yè)要求經過了完整的認證和發(fā)布。另一個重點是必須從最靈敏的阻值范圍內選取樣品。圖3顯示了薄膜電子設計的臨界邊緣,可做借鑒。
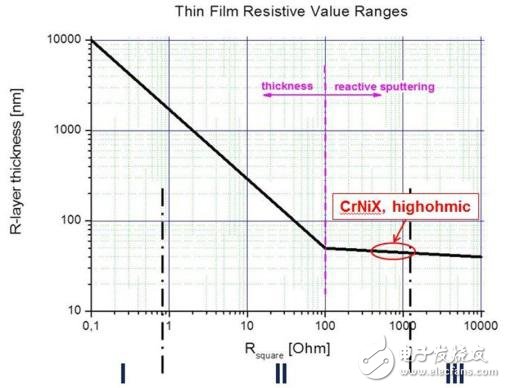
圖3: 不同阻值的電阻層厚度
方形電阻R□的整個阻值范圍使有三種合金(I,II和III)決定的。合金II采用的是CrNiX(X代表第三種元素)。1 Ω~100Ω之間的R□是通過改變2μm到30nm的電阻層厚度來實現的。在氧化和腐蝕同時發(fā)生時,電阻層的改變會引發(fā)不同的效應。較厚的電阻層會出現表面或顆粒邊界效應。相反,我們必須面對在薄電阻層上出現的體積效應,這種效應可以影響整個層的厚度。在氧化的情況下,所有電阻材料都會受到影響。在腐蝕的情況下,這會導致電阻層的徹底破壞。為了做試驗,我們挑選了這類敏感的樣品,保證樣品會出現最壞的情況(電阻類型有MINI-MELF, MMA0204,最大阻值為180 kΩ,R□大約是800 Ω)。
各個測量點是從20個測試樣品的單一結果得到的。為了實現統(tǒng)計覆蓋到全部事件(最壞情況)的98%,每個測試點的參數值的概率分布都進行了估值。
4.測試結果和主要發(fā)現
兩種不同電絕緣漆和兩個不同偏置電壓的測試結果見圖4。我們找到了兩個明顯的降級機理,可以區(qū)分老化(40 / 93, 70 / 90)和破壞性的腐蝕狀態(tài)(85 / 85)。
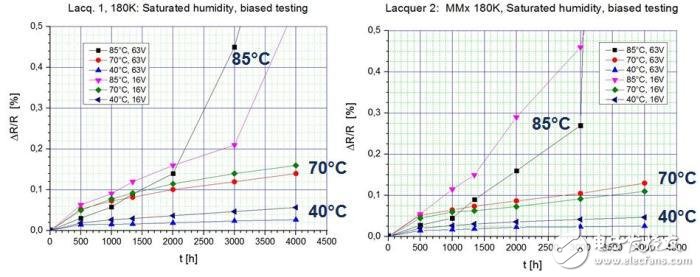
圖4: 在測試環(huán)境中暴露4000小時后的測試結果 (40 / 93, 70 / 90, 85 / 85)
在這個階段,還不能根據85 / 85測試數據做比較或預測。因此,為了使用可比較的數據,我們在0.07%到0.1%再到0.2%的ΔR / R低漂移水平上,提出了對所有阻值漂移進行標準化的方法。通過定義一個既明顯但又幾乎不會造成破壞的可接受且在標準要求內的漂移水平,我們就可以比較全部測試數據,另外還可以加上HAST 130的測試結果。標準化參數漂移的結果(在我們這個例子是ΔR / R)與相應的暴露時間參見圖5。暴露時間的標準化的各個測量點要么是直接推導出來的,或是經過我們不同的濕度測試,從120個獨立的ΔR / R漂移測量結果推算出來的。
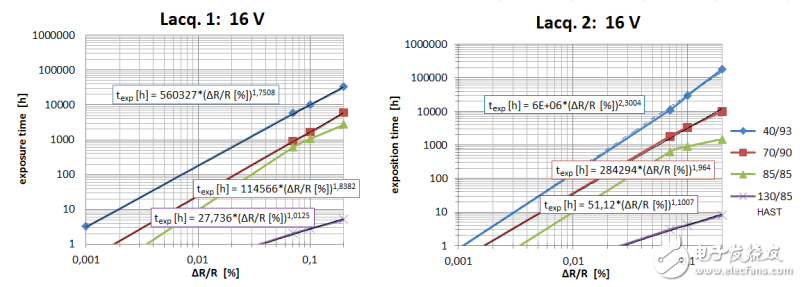
圖5: 在非破壞性的ΔR / R 水平上對測試結果進行標準化
每個參數的漂移從方方面進行了徹底的定義:幅度,系統(tǒng)/材料的關系,在規(guī)范內可接受的值,估計的元器件預期壽命。
對于180 kΩ的薄膜電阻,我們定義并選取ΔR / R of ≤ 0.2 %(我們估計:只有顆粒邊緣的氧化會改變電導率,在材料層上也沒有體積效應)。
經轉換后的第1種漆和第2種漆的測試數據見圖6(在這個階段,預估的RH設定值稍微有點差別,但沒有關聯(lián))。尤其是在較低的溫度下,漆的變化很明顯。曲線可能匹配指數函數,但匹配度不是很好,尤其是第1種漆。
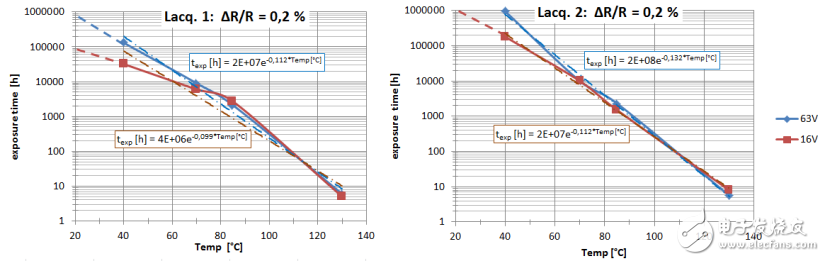
圖 6: 比較兩種漆的測試結果
5.嘗試使用現有模型
在很多論文和應用報告里,Lawson模型還是非常常用的的,尤其是評估有源元器件的潮濕加速動作。因此,為了評估我們的測試結果,我們選用了這個模型。我們使用Lawson建議的數值,比較在不同相對濕度rh (公式 1)下試驗結果的加速因子。
公式 1: 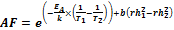
我們選用了第2種漆,因為它的指數趨勢線的線性相關最好。首先,我們把測量數據代到Lawson等式里,選定激活能EA (設為0.9 eV)和因子 b (設為1.0)。在測量溫度范圍內挑取幾個點,忽略相對濕度變化之間的偏置電壓,我們的結果是“不適合”,如圖7所示。
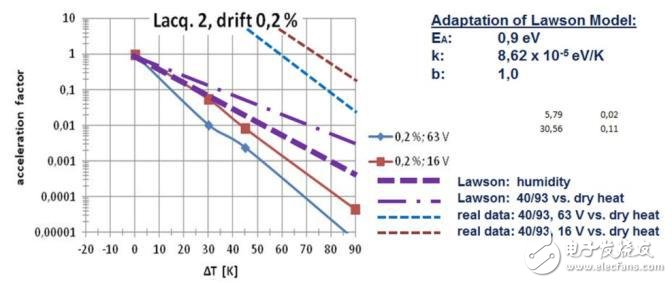
圖 7: 估算加速因子 (Lawson)
檢索現有文獻,Peck是提到的另一個作者。他改變了Lawson建議值,發(fā)現使用相對濕度能夠適應他自己的測試結果。在一篇文章里,Hallberg很好地概括了所有濕度測試和加速模型,包括他自己的。過去30年,他與Peck對濕度加速進行了大量研究。在很多出版物里都提到,他們的研究成果的適應性最好。圖8是Hallberg收集的可用模型。除了溫度意外,他們都使用相對濕度做為主要的測量參數。檢索最近幾年有關濕度加速的出版物,我們發(fā)現,人們還在使用與Hallberg和Peck 描述或收集的模型相同的或可比較的模型。

圖8
我們的目的是在很寬的不斷變化的溫度-時間-濕度范圍內,預測元器件的可靠性。因此,使用上面的模型并不能滿足我們的要求,因為在一定的相對濕度下,實際的含水量極大程度上取決于溫度。測量依賴溫度的實際含水量的指標是對應的蒸汽壓pvapor。這個數據可以從教科書里導出來。
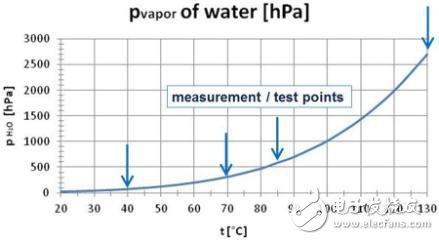
圖 9: 蒸汽壓與溫度
圖9顯示了溫度對pvapor (100 % RH)的依賴關系,包括我們在40℃、70℃、85℃和130℃下做試驗的測試點。在我們的試驗里,實際的蒸汽壓可以用pvapor x rh (例如在130℃: 2700 hPa x 0.85 = 2295 hPa)來直接計算。
5.1. 影響參數
仔細分析所研究的薄膜電阻的設計,推導出下面這些影響參數,如圖10到圖13所示。
電子元件一般是在芯部材料上覆蓋一層敏感的功能金屬層,外面再用密封、漆或塑模保護。我們的薄膜電阻有一個鋁、R層的底座或芯部材料,外面涂一層電絕緣漆,如圖10所示。元件的漆層直接暴露在測試或應用(例如85℃)的環(huán)境溫度下,不存在溫度梯度。水分子被吸收到漆的表面,吸收度取決于溫度。在漆層界面與外部環(huán)境之間存在壓差,壓差大小取決于實際的蒸汽壓。
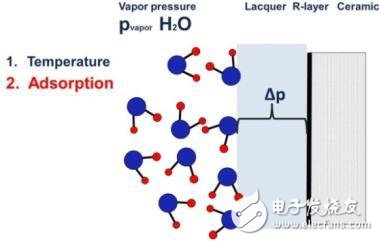
圖10: 水汽濃度,蒸汽壓
壓力平衡導致水或其他低分子物質的擴散到漆體里,如圖11所示。水或其他低分子量物質的匯集會擴大壓力擴散效應的界面面積。有水的時候,高溫和偏置電壓會加速氧化,在金屬層上產生電化學腐蝕,由于在層的表面存在電勢差,在最壞的情況下會在R層上產生電化學腐蝕。水濃度對溫度依賴程度較高,因此在熱和偏置的狀態(tài)下,器件被破壞的風險較高。
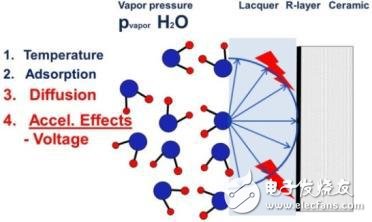
圖11:蒸汽擴散,施加電壓加速
當施加電功率時,會發(fā)生特殊的減速效應。電功率會被轉換成電阻層里的焦耳熱。電阻層的溫度會比環(huán)境溫度高一點,減緩了在漆里面和界面上水匯集處的擴散(見圖12)。
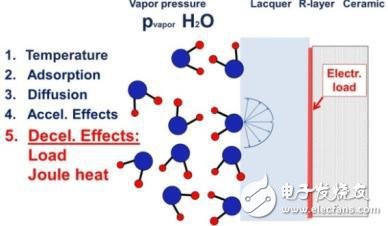
圖12: 焦耳熱減緩擴散
這就解釋了由于相應的負載和焦耳熱分別在漆里面和R層里面影響擴散過程,較高電壓的電阻樣品降級速度較慢的現象。最后,在漆里面失效或缺陷的地方(氣泡,空洞,小孔或由表面引腳的分層引起本地擴散),會強化或引發(fā)毀滅性的的加速,如圖13所示。
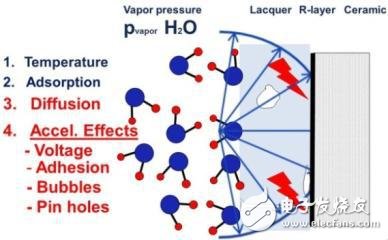
圖 13: 缺陷加速
我們可以得出結論,對于特性降級和預測特性降級,在給定R層或金屬系統(tǒng)時,漆或塑模的參數是決定性因子:
· 由吸附作用造成水汽滲透,進而形成水分子的移動?擴散;
· 漆的可靠性是由低分子物質的擴散速度決定的;
· 為了在漆里保持氣體擴散,需要有凈容積;
· 依賴于溫度和漆的有機鏈段的移動,在擴散的使用和加速過程中會產生新的凈容積;
· 在界面上或漆里面的空洞會提高濃度梯度,減緩擴散。
圖14顯示把測試數據首先臨時轉換成與工況有關的依賴于Lawson的模型:標準化ΔR / R ≤ 0.2 %:暴露時間texp與蒸汽壓pvapor。這個臨時模型使用明確的物理量pvapor而非RH。溫度與相應的蒸汽壓部分相關。可以推導出加速因子,以年來表示。
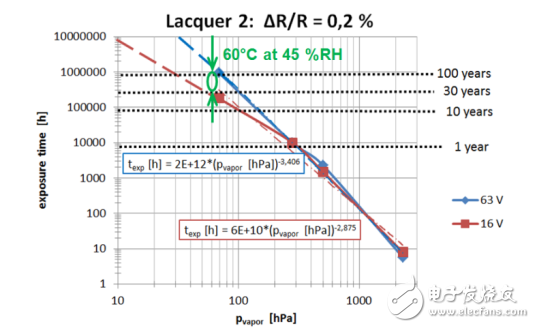
圖 14: 蒸汽壓加速,預測
現在可以回答有關預測的要求了。例如,“在60 °C和45% RH下,保持ΔR / R of ≤ 0.2 %的使用時間有多長?”通過簡單的計算,199 hPa * 0.45 ?90 hPa (數據pvapor 見圖9),就可以直接得出在現場的實際偏置濕度條件下,暴露時間可以達到15到30年,如圖14所示。
這個模型沒有全面考慮水擴散對溫度的依賴,尤其是較高的溫度和低蒸汽壓的情況。另一個物理方法能夠更好地考慮這個影響和實際擴散的依賴以及吸附,這個方法是必需的。
6.通用模型:在溫度-濕度-時間域內標準化參數漂移
6.1. 基礎模型
在我們的前期工作總發(fā)現與時間有關的Arrhenius函數是重大成果,基于這個成果我們開發(fā)出了下面的通用模型。
與時間相關的物理過程有很多,可以用Arrhenius定律來描述。擴散是其中之一。在干熱條件下,用依賴時間的漂移做為漆/塑模擴散特性的關鍵參數已經強調得很多了,在前面的章節(jié)也得出結論。在高濕度環(huán)境條件下的測試,這一點需要更加強調。
Sinnadurai等人已經在厚膜電阻上做了類似的觀察,研究通常的老化動作。他們認為,擴散主要是由一些隨時間的平方根而變化的老化參數引起的,與導熱過程受擴散控制的降級相符。
擴散機制是教科書的內容:
公式2給出了擴散長度Ld,D是擴散系數或擴散率,t是(暴露)時間。
公式 2: 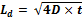
對ΔR / R ≤ 0.2 %漂移的標準化已經把我們導向用相應的暴露時間texp來描述上面的情形。公式3顯示使用公式2以后,Ld成為電絕緣漆層xlacq的厚度。
公式 3: 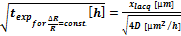 這里ΔR/R小于0.2 %.
這里ΔR/R小于0.2 %.
圖15和16是試驗結果,轉換成依賴于溫度倒數1/T的√texp,以便帶入Arrhenius形式,能夠直接讀出EA / k。
這里,我們把40 / 93 和70 / 90與85 / 85和HAST130的數據分開。這樣就對應前面出現和描述的老化和腐蝕效應。我們根據擴散過程研究出新的建模方法,看起來很有前途。
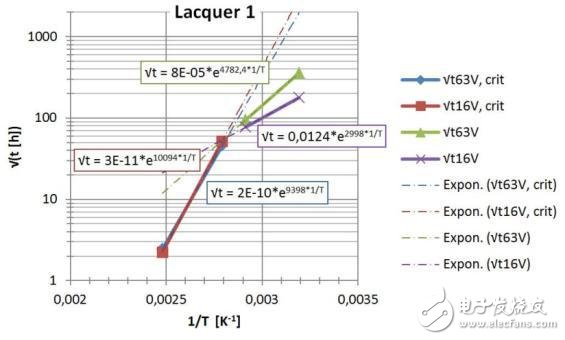
圖 15: 第一種漆: 測試數據轉換成塑模數據
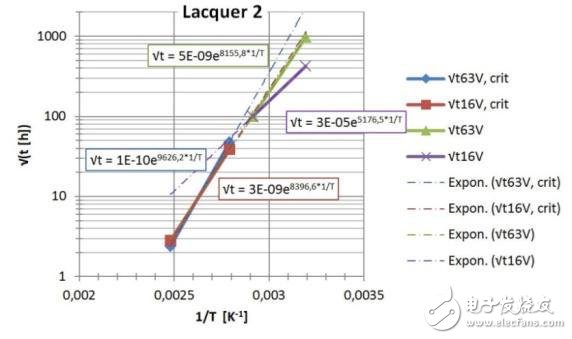
圖 16: 第二種漆: 測試數據轉換成塑模數據
6.2. 開發(fā)模型
擴散可以分成與時間相關和與時間無關的兩種情況,如圖17所示。擴散長度是描述擴散問題的特征參數,隨暴露時間的平方根√texp而增加。
如果擴散的長度短于漆或塑模的厚度,在金屬層表面或在我們案例里漆和R層的界面的水汽濃度會大不相同(見圖17,左圖)。由于在漆的厚度方向水汽濃度的梯度大,在界面處的濃度與時間高度相關。
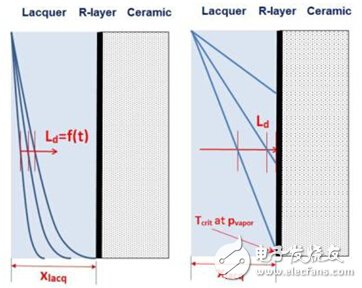
圖17: 擴散: Ld
如果漆或塑模的厚度小于擴散長度(見圖17,右圖),在漆里面濃度分布基本上是線性的。在一定的溫度和蒸汽壓力下,界面上的水汽濃度會變高。溫度會在金屬層上持續(xù)產生腐蝕效應。然而,水汽濃度再提升并不會進一步加快腐蝕進程。我們把界面處的濃度閾值用溫度Tcrit 和Tcrit eff來表征。
Cussler提出了一個描述氣體里在兩個不同壓力(但溫度相同)下自擴散的經驗公式: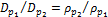 。這里ρ是氣體密度(量綱:kg/m3)。為了讓我們的模型簡單,我們建議使用簡化的估算公式4。
。這里ρ是氣體密度(量綱:kg/m3)。為了讓我們的模型簡單,我們建議使用簡化的估算公式4。
公式 4 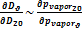
把簡化的公式4和公式5的經驗關系組合起來,我們引入蒸汽壓力,算出影響過程的參數。最后,公式5完整描述了整個模型。
公式 5: 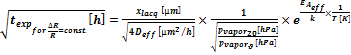
… 或 … 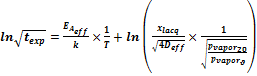
正如圖15和圖16已經顯示的,我們的試驗數據對擴散建模方法吻合得很好。因此,有關的擴散過程可以用一個模型來描述。新模型的基礎從公式5的第二個版本推導出來的ln√t – 1 / T關系圖。
圖18里的圖在臨界溫度的倒數1 / Tcrit斜線分成與時間無關(左)和與時間相關(右)的兩個部分。在幾乎100%飽和的濕度條件下,溫度相關性用兩個線性特征參數來定義,分別在ln√t – 1 / T關系圖里與時間相關和與時間無關的地方。這兩條線表征了在偏置濕度下可能的暴露時間的最壞情況。
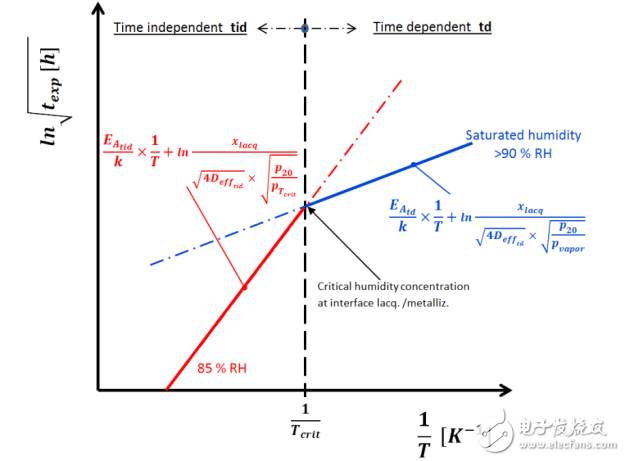
圖 18: 在時間相關和時間無關區(qū)域的濕度降級
當在圖里加入干熱特征時(按照與時間相關的Arrhenius定律方法推導),線性度非常好,如圖19所示,這很好地表明擴散在干熱老化機制里也是一個主要影響參數。當用計算方法標準化對漂移的時間相關性進行補償時,干熱特征只是被驅動的因素,用功能層的活化因子EA來定義。擴散條件是恒定的,與我們在ln√t – 1 / T圖與時間無關區(qū)域里水飽和界面情況下發(fā)現的情形是一致的。
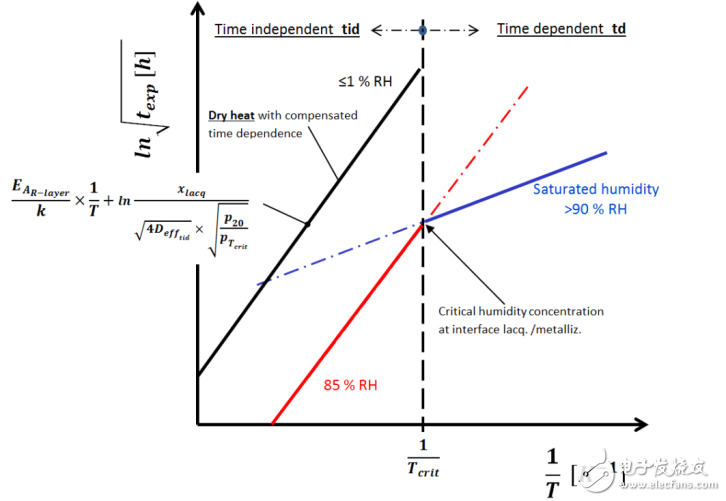
圖 19: 在 ln√t – 1 / T圖里的干熱特性
通過這兩步,就可以導出圖20所示的通用模型。
在與時間無關區(qū)域,當水汽濃度超過臨界值時,功能層(在我們的案例里是電阻膜)的活化能EA將受到溫度和相應的表面電勢差的影響,用Δ(EAbias/k)來表達。斜坡特性曲線可以認為與干熱曲線平行,氧化/腐蝕速度與時間無關,但或者非常依賴于一種極端情況,或是在另一邊水濃度非常低的區(qū)域。
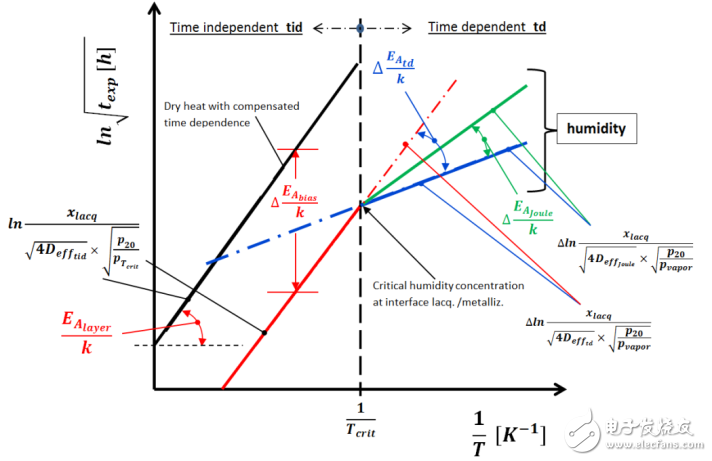
圖20: 元器件溫度/濕度老化特性的通用模型
在有偏置濕度的情況下,由于在漆層界面上水汽濃度與時間有關,溫度在圖內與時間有關區(qū)域的影響是減小的。封裝材料在擴散上的依賴性用ΔEAtd 和lnΔ√(x / 4D 。.)td這兩個影響因子來表達。電負載轉換成焦耳熱可以用減速因子EAjoule來表達,在前面圖12已經解釋過了。
為了評估吸附的影響(見圖10),我們再次利用了教科書的知識。水分子的數量是由一側的絕對濕度決定的(由于達到漆或塑模表面的水蒸氣的速率較高,更高的水濃度會導致更高的吸附率),和另一側的溫度(更高的溫度導致更高的吸附率)。綜合考慮這兩個作用方向相反的因素,意味著在表面的水含量會達到一個平衡狀態(tài),主要是由空氣中的相對濕度rh(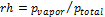 )決定的。
)決定的。
在模型里引入吸附率依賴度,見圖12。在與時間有關的區(qū)域,與吸附有關的特性在rh ≤ 0.93的幾乎飽和濕度這個極端,和rh 幾乎為0的區(qū)域內擺動,取決于實際存在的相對濕度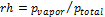 。
。
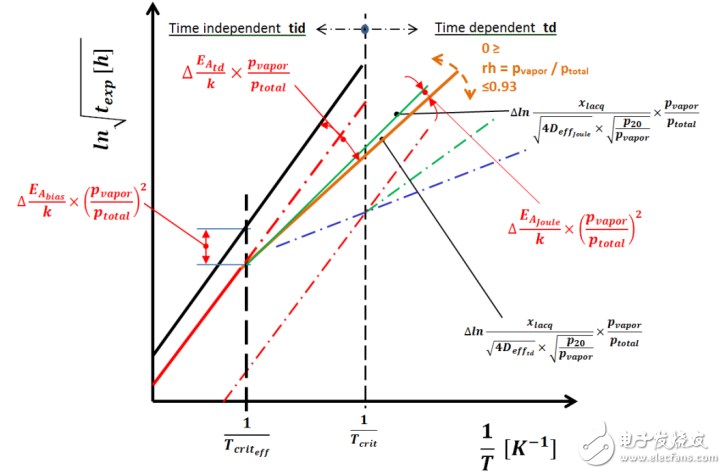
圖 21: 吸附的影響; rh 特性在td 和干熱現之間輪換
整個rh的依賴范圍在飽和濕度和干熱之間,可以用公式6到公式8定義與時間有關的情況,公式9和公式10用于與時間無關的情況。在大括號里的項表示了與濕度有關的方面。
公式 6: 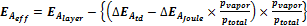
for T < Tcriteff, i.e. for time-dependent processes;
公式 7: 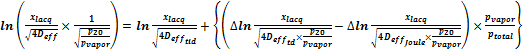
for T < Tcriteff , i.e. for time-dependent processes;
公式 8: 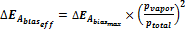 ;
;
(經驗公式,用于T > Tcrit eff條件下與時間無關的過程)。
公式 9: 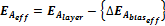
用于 T > Tcriteff, 與時間無關的的過程;
公式10: 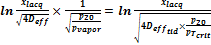 用于 T ≥ Tcriteff, 與時間無關的的過程;
用于 T ≥ Tcriteff, 與時間無關的的過程;
為了防止和檢驗這個線性rh 依賴度是否對我們的模型也有效,對第1種漆和第2種漆進行了另一個偏執(zhí)濕度測試。選擇的條件是90 °C和 40 % RH (pvapor = 280 hPa),恰好與前面在70 °C和90 % RH下測試的蒸汽壓力一樣。測試結果帶入圖22和圖23的ln√t – 1 / T圖(看綜合星號,0.40 rh at 90 °C,1/T = 0.00275 K-1)
我們的結果證實實際的吸附率與實際的相對濕度rh成正比。對于給定的溫度,在干熱和幾乎飽和濕度td (rh 約為 0.90 至0.93)暴露時間Δln√texp的結果差異顯示在與時間相關的區(qū)域,與rh線性相關,見圖22和23。對于給定的rh ,得出的新特性落在td 的特性線和與干熱相關的實際rh 數據之間。計算得出的rh = 0.4棕色破折線恰好穿越90°C, 40 % RH的實際測試點。
在公式8的時間無關區(qū)域,推導出二次方程,從我們的測試結果的經驗數據估計出來。在時間無關區(qū)域檢驗在較低rh的適用性,要在今后的研究中獲得更堅實的測試數據。
在幾乎所有的技術應用里,電子元器件會在溫度超過100 °C的正常大氣壓下工作。因此,出于實際需要,會在達到元器件的上限溫度內,通常在與時間相關區(qū)域內進行所有預測。
公式11和公式12描述了估算擴散Deff 的系數,以及臨界溫度相關涂漆或塑模系統(tǒng)的Tcrit 或 Tcrit eff。
公式 11: 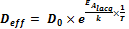
公式 12: 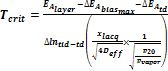 或
或 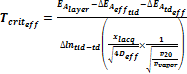
為了簡化計算,這里Deff事實上是表達的是滲透率(S0 x D0),包括與溫度相關的氣體溶解S,是對漆/R層界面上的實際水汽濃度的相對測量。
相關材料數據或功能信息可以直接從ln√t – 1 / T圖讀出來,或可以給給出的公式簡單地算出來。
6.3.實際使用模型和ln√t – 1 / T圖
我們把具體測量數據轉換到圖19和圖20。我們在給定的電阻膜材料上使用了兩種不同的漆,現在可以完全顯示其特性,并且可能在整個規(guī)定溫度-濕度-時間域內做預測。
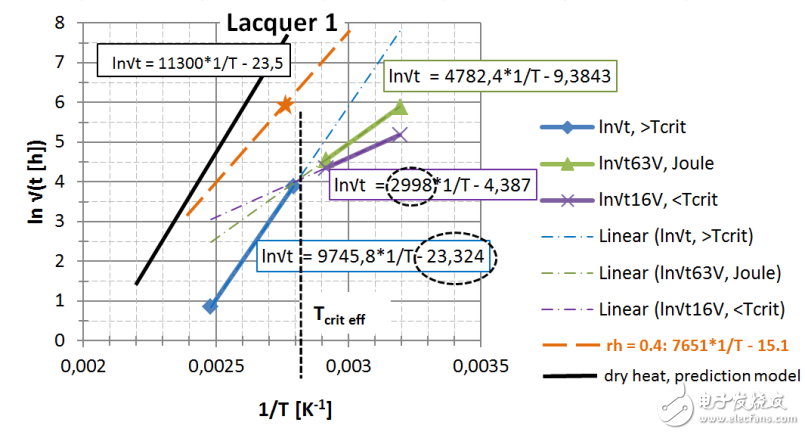
圖 22: 第一種漆, 直接讀出 EA / k 和ln{xlacq /√(4D x …)}, 用虛線框起來
可以獲得以下數據:
A. 塑模 / 漆:
· 擴散系數 D0, Dt crit 和 D20;
· 擴散過程的活化能 EA lacq;
· 電負載的減速效應 (焦耳熱) ΔEAJoule;
· 臨界溫度 Tcrit 是一個特性;
· 有效的臨界溫度 Tcriteff, 與討論的具體情況相關。
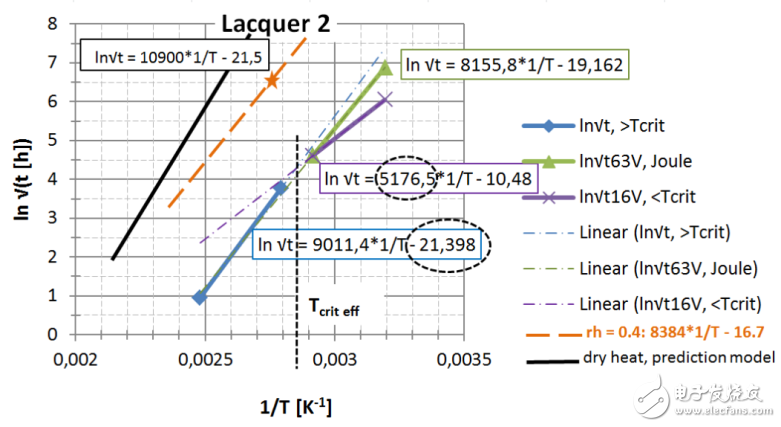
圖 23: 第2種漆,直接讀出 EA / k 和ln{xlacq/√(4D x …)}, 用虛線框起來
B. 功能層 (金屬層):
· 活化能EAlayer;
· 偏置電壓加速效應 ΔEAbias, 在層界面上達到臨界水汽濃度時;
· 非臨界暴露時間texp最大值的預測工具,對于每個給定的溫度、濕度和負載條件。
示例:
現在我們可以用具體數據估計和比較第1種和第2種電絕緣漆。
未來,我們可以預測現場或測試應用的情況,如在130 °C (T = 403.12 K) 和 155 °C (T = 428.12 K)工作溫度、最小負載,以及最壞氣候條件41 °C和 75 % RH下的電氣應用。
結果見下表。
給定R層的活化能是相同的,可以用EAlayer / k直接讀出,如?EAR-layer = 0.96 eV。
計算最大與時間無關的偏置濕度加速,做為差值ΔEAbias = 0.16 eV。
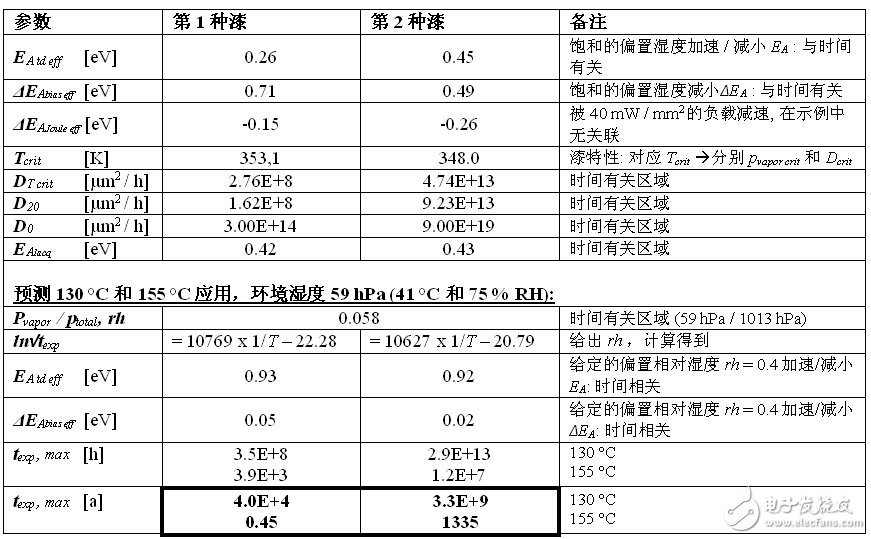
*) 備注:有記錄的最高溫度和濕度是2000年在沙特阿拉伯的Dharhan,溫度是41℃,濕度超過70 %( pvapor = 59 hPa; 41 °C / 100 % RH: 78 hPa)。
結果:
兩個材料在兩個環(huán)境條件下都出現了差異。然而,即便在更糟的自然氣候條件下和130℃的環(huán)境溫度下,預計壽命也分別達到4000年或33E+9年,比現場使用對元器件的實際要求高得多。在155℃環(huán)境溫度下,這些被調查的電絕緣漆之間特性的差異變得十分明顯。
結論
-偏置濕度可以是破壞性的,即便滿足了標準(AEC-Q200)的官方要求。
-獨立的85 / 85或HAST測試只適用于評估耐潮能力的相對比較,對推測所研究的薄膜電阻系統(tǒng)沒有幫助。兩種測試都可能是破壞性的。
-對環(huán)境里達到非破壞性的漂移水平的暴露時間進行標準化,用于新的預測模型。
-分配蒸汽壓力,直接讀取允許的暴露或加速因子上的信息,就可以產生一個簡單實用的預測工具。
-公開的模型(如Lawson)不適用于薄膜電阻,也不使用通用方法和與濕度加速有關的問題。
-相對濕度是一個描述實際吸附率的重要參數,在試驗研究里其影響無疑是可度量的。其他作者根據rh依賴度設計出模型,在一些使用模塑或功能材料的特定情況下已經被采納。因此他們的結果模型一定是不同,并且只有在不變的模塑材料和功能層的激活能情況下才有效。他們沒有考慮到重要的各個擴散情況和系統(tǒng)的氧化特性。
-我們的模型遵從與擴散有關的系統(tǒng)特性,如本文所討論的涂層材料的實際密封特性。
-像85 / 85 或HAST測試的標準要求可以用客觀數據對實際應用需求和器件使用條件進行評估;
-模型和ln√t – 1 / T圖的描述是從對薄膜電阻的試驗研究推導的,將會形成廣泛影響,被轉換用于所有模塑或涂漆的有熱或濕度有關降級效應和健康預測的有源和無源元器件。
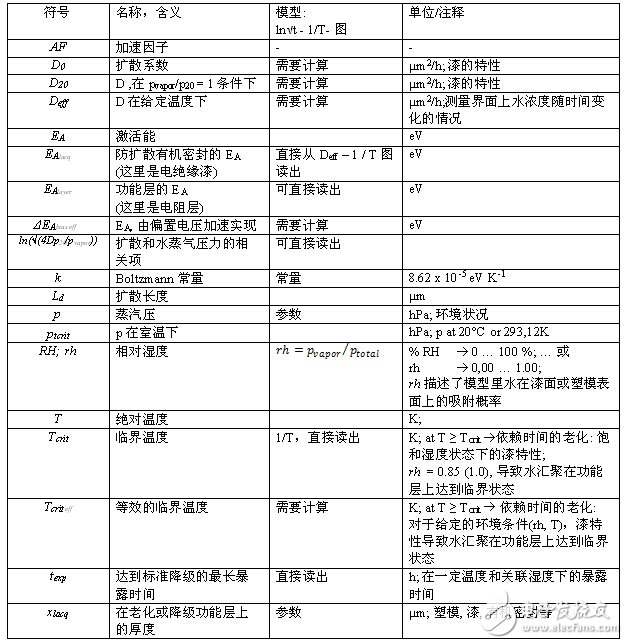
附錄:符號表及其含義/解釋
 電子發(fā)燒友App
電子發(fā)燒友App

























評論