內(nèi)在可編程的硅 MEMS 時(shí)鐘振蕩器架構(gòu)能夠幫助采用 FPGA 的系統(tǒng)設(shè)計(jì)人員解決許多難題。這種微型機(jī)電系統(tǒng)架構(gòu)能夠輕松整合一些其它功能,如:用于消減 EMI 的擴(kuò)頻時(shí)鐘、用于消除抖動(dòng)的數(shù)控振蕩器以及高速應(yīng)用中的失效保護(hù)功能。
2013-08-15 11:12:08 2524
2524 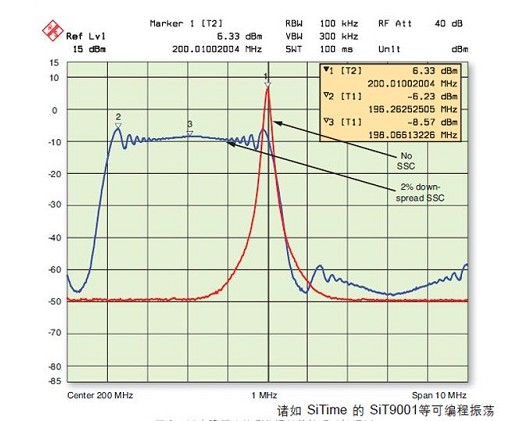
您好,數(shù)據(jù)表顯示PIC的最大速度是40MHz,但是欠振蕩器配置或第二章數(shù)據(jù)表沒(méi)有提供任何關(guān)于使用40MHz振蕩器的信息?我的選擇是什么?謝謝您,
2020-03-31 09:22:43
公式Aβ=1<-180°中的180°相移是由有源元件和無(wú)源元件引入的,像任何精心設(shè)計(jì)的反饋電路那樣,使振蕩器取決于無(wú)源元件的相移,因?yàn)樗_且?guī)缀醪黄啤?yīng)使由有源元件提供的相移最小,因?yàn)樗S濕度而
2015-01-05 10:15:44
想復(fù)現(xiàn)論文中的這個(gè)振蕩器,但是仿真出來(lái)的結(jié)果是這樣的,開(kāi)關(guān)合上或者關(guān)閉后振蕩幅度會(huì)越來(lái)越小,然后就不振蕩了,請(qǐng)問(wèn)問(wèn)題出在哪里?
2022-06-23 23:32:11
你好我正在設(shè)計(jì)我的第一個(gè)斯巴達(dá)6 FPGA板。我對(duì)外部振蕩器/時(shí)鐘有幾點(diǎn)懷疑。我瀏覽了時(shí)鐘資源指南UG382,但它沒(méi)有多大幫助,因?yàn)樗饕枋隽?b class="flag-6" style="color: red">FPGA的內(nèi)部電路,一旦你選擇了振蕩器就會(huì)
2019-06-12 14:21:39
時(shí)序?qū)τ谑澜缟蠋缀跻磺须娮討?yīng)用都至關(guān)重要。振蕩器廣泛用于各種應(yīng)用,用于控制微處理器,MCU,SoC以及其他許多器件或電路的時(shí)序。不同應(yīng)用需要不同類(lèi)型的振蕩器。常常有些問(wèn)題可通過(guò)某種類(lèi)型的振蕩器來(lái)
2018-11-01 15:41:19
,使其成為測(cè)試設(shè)備和衛(wèi)星通信應(yīng)用的理想選擇。寬頻率范圍低相位噪聲低諧波無(wú)線(xiàn)廣播基地臺(tái)移動(dòng)通訊CLV0795E-LF振蕩器CLV0835E-LF振蕩器CLV0975B-LF振蕩器CLV0915A-LF
2021-04-03 16:46:07
`CRO或陶瓷諧振器系列振蕩器以提供出色的相位噪聲性能而聞名。 它們?cè)诜秶鷥?nèi)可用從400 MHz到8 GHz的任何頻率,同時(shí)提供非常低的調(diào)諧靈敏度以?xún)?yōu)化性能。 獨(dú)特的構(gòu)造CRO振蕩器及其實(shí)現(xiàn)低調(diào)
2021-04-03 16:50:57
`DRO系列壓控振蕩器是一種基本的窄帶信號(hào)源,它利用高Q介質(zhì)諧振器實(shí)現(xiàn)了最佳的相位噪聲性能。目前,DRO VCO解決方案適用于在7至14 GHz范圍內(nèi)工作的頻率。該可定制的超低噪聲振蕩器系列可提供
2021-04-03 16:55:11
我用PIC16F68 4-ICD適配器模塊為我的ICD3。是否需要使用外部振蕩器進(jìn)入調(diào)試模式?我的目標(biāo)電路(使用PIC16F684)不使用外部振蕩器(我的軟件只使用內(nèi)部振蕩器和時(shí)鐘芯片中斷)。謝謝!
2020-03-12 12:55:11
。振蕩器是RFID射頻前端的關(guān)鍵模塊,低功耗和小體積是RFID的兩個(gè)重要性能指標(biāo)[3-4]。但目前射頻振蕩器主要采用壓控振蕩器(VCO)[5],由于VCO同時(shí)采用晶體管和二極管兩個(gè)有源器件,很難滿(mǎn)足RFID對(duì)低復(fù)雜度的要求,需要針對(duì)RFID研究新的振蕩器設(shè)計(jì)方法。
2019-08-05 08:21:17
STM32的外部振蕩器失效怎么解決?
2021-11-16 06:15:12
計(jì)低相位噪聲線(xiàn)性調(diào)諧倍頻帶寬應(yīng)用微波收音機(jī)直接廣播V602ME55-LF振蕩器V585ME66-LF振蕩器V602ME15-LF振蕩器V585ME28-LF振蕩器V602ME33-LF振蕩器
2021-04-03 16:26:03
嗨,我想知道其他人是否遇到了同樣的問(wèn)題。在一個(gè)小型測(cè)試系統(tǒng)中,我使用12MHz的晶體,用適當(dāng)?shù)碾娙萜髯鳛橥獠?b class="flag-6" style="color: red">振蕩器,用18F25K50芯片。使用XS振蕩器設(shè)置,振蕩器將無(wú)法啟動(dòng)。我嘗試了中等
2020-04-26 13:59:16
請(qǐng)教有關(guān)振蕩器的知識(shí)?什么是對(duì)稱(chēng)的?什么是非對(duì)稱(chēng)的?什么是多諧的?
2009-04-23 18:49:10
本帖最后由 o_dream 于 2020-9-15 10:16 編輯
今天將要給大家介紹一種RC振蕩器Twin-T振蕩器,它產(chǎn)生正弦波輸出以用于類(lèi)似于Wein-bridge振蕩器的固定頻率
2020-09-15 10:04:18
隨著科學(xué)技術(shù)的發(fā)展,越來(lái)越多的振蕩器和天線(xiàn)集成在一起。小型化設(shè)計(jì)通常要求將多種器件集成到普通、緊湊的結(jié)構(gòu)中。那么大家知道,什么是集成振蕩器式有源天線(xiàn)嗎?
2019-08-06 07:32:21
描述7404振蕩器使用 TTL IC 制成的振蕩器,其中使用 7404,這是一種專(zhuān)門(mén)設(shè)計(jì)用于執(zhí)行逆變器功能的 IC。除了集成的 7404 之外,該振蕩器的電路還使用無(wú)源元件、電容器和電阻器。示意圖PCB
2022-06-23 06:25:09
最近在學(xué)習(xí)振蕩器,但是對(duì)于振蕩器里面各個(gè)參數(shù)是如何準(zhǔn)確計(jì)算出來(lái)很有疑問(wèn),參考IEEE里面的論文,里面的內(nèi)容在圖片上,我想請(qǐng)教各位公式部分是怎么得出來(lái)的,以及振蕩器設(shè)計(jì)的計(jì)算過(guò)程有什么需要注意的嗎
2016-03-17 14:36:36
壓控振蕩器 1、壓控振蕩器的基本原理:通過(guò)改變控制電壓改變變?nèi)荻O管的電容
2009-06-29 14:09:46
所以我最近購(gòu)買(mǎi)了ML405開(kāi)發(fā)板,我現(xiàn)在需要找到一個(gè)與userclk一起使用的振蕩器。該手冊(cè)規(guī)定我需要一個(gè)“接受3.3V的半插座LVTTL振蕩器”。然而,在我搜索Digikey和Mauser時(shí),我
2019-08-14 07:15:17
想請(qǐng)教一下大佬些,我需要一個(gè)變頻1-100hz的垂直振蕩器我需要用到哪些東西呀,剛?cè)腴T(mén)不是很懂。可以把那些電機(jī)的信號(hào)和振蕩器,變頻器的型號(hào)說(shuō)一下嗎。預(yù)算不是很充分在4-500塊
2023-03-24 01:01:51
將電源線(xiàn)插頭插入振蕩器對(duì)應(yīng)的插孔內(nèi),然后將插頭插入電源插座中,此時(shí),電源接通,如需要水平振蕩則打開(kāi)水平振蕩開(kāi)關(guān);如需要垂直振蕩則打開(kāi)垂直振蕩開(kāi)關(guān)。振蕩速度可根據(jù)您的要求調(diào)整速度旋鈕。
2019-10-14 09:11:20
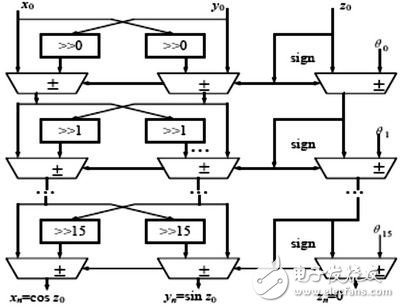
正余弦信號(hào)的實(shí)現(xiàn)過(guò)程,給出了在FPGA 中設(shè)計(jì)數(shù)控振蕩器的頂層電路結(jié)構(gòu),并根據(jù)算法特點(diǎn)在設(shè)計(jì)中引入流水線(xiàn)結(jié)構(gòu)設(shè)計(jì)。在正交數(shù)字混頻器中,采用數(shù)字頻率合成技術(shù),可以將數(shù)字處理延續(xù)到正交調(diào)制之后或正交解調(diào)
2021-07-15 08:00:00
基于FPGA的壓控振蕩器是否能夠?qū)崿F(xiàn),相關(guān)文獻(xiàn)或論文有沒(méi)有,求大神指導(dǎo)
2014-12-02 14:09:21
1 基于 DSP 的數(shù)字振蕩器的設(shè)計(jì)與實(shí)現(xiàn) 基于 DSP 的數(shù)字振蕩器的設(shè)計(jì)與實(shí)現(xiàn) 黃福瑩 陳華 徐金隆 廣西大學(xué)計(jì)算機(jī)與電子信息學(xué)院 南寧 530004 摘要 摘要 本文闡述了一種基于 DSP
2021-08-09 06:51:03
`多諧振蕩器:這個(gè)圖中間不能交叉怎么畫(huà),求圖`
2017-05-04 15:27:34
多諧振蕩器PPT課件又稱(chēng)無(wú)穩(wěn)態(tài)電路。主要產(chǎn)生各種方波或時(shí)鐘信號(hào)。5.3.2 不對(duì)稱(chēng)(CMOS)多諧振蕩器RC環(huán)形多諧振蕩器5.3.4 石英晶體多諧振蕩器5.4.1 微分型單穩(wěn)態(tài)觸發(fā)器5.4.2 集成單穩(wěn)態(tài)觸發(fā)器5.4.4 單穩(wěn)態(tài)觸發(fā)器的應(yīng)用
2009-09-24 09:43:38
描述多諧振蕩器什么是多諧振蕩器?mutivibrator這個(gè)名稱(chēng)指定了一組廣泛應(yīng)用于開(kāi)關(guān)的電路,如移位寄存器或臨時(shí)存儲(chǔ)器,以及定時(shí)振蕩器或時(shí)鐘的方波。這些電路基本上是使用反饋操作的閉環(huán)反饋
2022-08-24 06:05:54
`如何使用逆變器設(shè)計(jì)環(huán)形振蕩器...求大佬幫幫忙`
2021-06-17 12:26:25
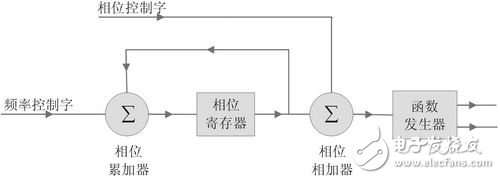
本文介紹如何用FPGA(現(xiàn)場(chǎng)可編程邏輯門(mén)陣列)和SRAM(靜態(tài)隨機(jī)存儲(chǔ)器)實(shí)現(xiàn)高精度數(shù)控振蕩器。
2021-05-08 09:30:28
大家好!有一種方法可以禁用PIC18F67 J50的內(nèi)部振蕩器嗎?我正在使用兩種功率模式,一種是全功率的8MHZ+PLL,另一種是低功率模式下的TMR1振蕩器的32.768KHz。閱讀數(shù)據(jù)表39775c,我發(fā)現(xiàn)我可以禁用PLL,但是找不到禁用8MHz內(nèi)部振蕩器的方法。
2019-10-15 12:28:41
時(shí)鐘系統(tǒng)存在的意義是什么?常見(jiàn)的振蕩器有哪些?
2022-01-20 06:29:51
我正在開(kāi)發(fā)代碼(PIC32 MZ),以便在一系列開(kāi)發(fā)PCB上運(yùn)行。有些有12MHz的振蕩器和24MHz的振蕩器。有人能建議一種代碼檢測(cè)方法嗎?
2019-10-28 13:56:41
我一直在和PIC24FJ128DA210一起工作,我試圖用MCC來(lái)設(shè)置系統(tǒng),當(dāng)我檢查代碼時(shí),我看到有一個(gè)函數(shù)來(lái)初始化振蕩器,我有:我只想驗(yàn)證我是否正確地設(shè)置了振蕩器,我對(duì)振蕩器了解得更多從8位微控制器寄存器,但是,我需要了解如果我需要固定振蕩器設(shè)置。我有一個(gè)內(nèi)部振蕩器(8Mhz)與鎖相環(huán)模塊啟用。
2020-04-09 14:26:36
晶體振蕩器是指從一塊石英晶體上按一定方位角切下薄片(簡(jiǎn)稱(chēng)為晶片),石英晶體諧振器,簡(jiǎn)稱(chēng)為石英晶體或晶體、晶振;而在封裝內(nèi)部添加IC組成振蕩電路的晶體元件稱(chēng)為晶體振蕩器。其產(chǎn)品一般用金屬外殼封裝,也有
2021-08-09 06:46:27
復(fù)位是什么意思?時(shí)鐘可分為哪幾種?時(shí)鐘有什么作用?晶體振蕩器有哪些功能及用途?晶體振蕩器的特性是什么?
2021-07-01 07:38:04
晶體振蕩器也分為無(wú)源晶振和有源晶振兩種類(lèi)型。無(wú)源晶振與有源晶振(諧振)的英文名稱(chēng)不同,無(wú)源晶振為crystal(晶體),而有源晶振則叫做oscillator(振蕩器)。無(wú)源晶振需要借助于時(shí)鐘電路才能
2013-06-09 11:52:27
晶體振蕩器的選用 晶體振蕩器被廣泛應(yīng)用到軍用及民用通信電臺(tái),微波通信設(shè)備,程控電話(huà)交換機(jī),無(wú)線(xiàn)電綜合測(cè)試儀,BP機(jī)、移動(dòng)電話(huà)發(fā)射臺(tái),高檔頻率計(jì)數(shù)器、GPS、衛(wèi)星通信、數(shù)字收音機(jī)、機(jī)頂盒、無(wú)線(xiàn)局域網(wǎng)
2012-10-05 14:22:52
目錄晶體與晶振晶體晶振恒溫晶體振蕩器(OCXO,Oven Controlled Crystal Oscillator)關(guān)鍵參數(shù)溫度補(bǔ)償晶體振蕩器(TCXO)普通晶體振蕩器(SPXO)壓控晶體振蕩器
2021-07-28 06:40:02
怎樣去設(shè)計(jì)一款壓控振蕩器?壓控振蕩器在射頻通信電路中的應(yīng)用是什么?
2021-06-04 07:17:00
外觀測(cè)溫原理用一個(gè)高溫度系數(shù)的振蕩器確定一個(gè)門(mén)周期,內(nèi)部計(jì)數(shù)器在這個(gè)門(mén)周期內(nèi)對(duì)一個(gè)低溫度系數(shù)的振蕩器的脈沖進(jìn)行計(jì)數(shù)來(lái)得到溫度值。計(jì)數(shù)器被預(yù)置到對(duì)應(yīng)于-55攝氏度的一個(gè)值。如果計(jì)數(shù)器在門(mén)周期結(jié)束前到達(dá)
2022-02-11 07:32:45
一種待殊的振蕩器通常稱(chēng)為壓控振蕩器或VCO。VCO就是可以對(duì)應(yīng)輸入電壓變換輸出正弦波頻率的振蕩器。VCO的方框圖如下圖所示。它們?nèi)绾喂ぷ麟S著作用于VCO的電壓變化,VCO的輸出頻率改變。不像個(gè)固定
2017-12-06 14:03:45
大家好,我目前正在研究FPGA的溫度分布測(cè)量,我們的想法是使用分布式環(huán)形振蕩器(RO)和計(jì)數(shù)器來(lái)測(cè)量不同位置的FPGA溫度。問(wèn)題是:當(dāng)我在FPGA上放置一些振蕩器塊并在器件上編程時(shí),它們的輸出(RO
2018-11-09 14:10:53
`關(guān)于這個(gè)電路怎么計(jì)算A,B輸出的信號(hào)大小和周期?求大神解決。這跟集基耦合振蕩器相似 。`
2013-10-10 14:10:33
有源晶振也稱(chēng)之為石英振蕩器,因?yàn)槭⒕纫哂谔沾傻木龋裕械?b class="flag-6" style="color: red">振蕩器材質(zhì)均為石英所成。石英振蕩器根據(jù)晶振在電路中不同的功能又分為溫補(bǔ)振蕩器,壓控振蕩器,普通振蕩器,壓控溫補(bǔ)振蕩器。溫補(bǔ)
2016-06-08 09:46:37
石英晶體振蕩器石英晶體振蕩器晶體振蕩器上圖是經(jīng)過(guò)簡(jiǎn)化的電路圖并表明了石英晶體振蕩器的基本組成元件。石英晶體振蕩器中的放大器由至少一個(gè)驅(qū)動(dòng)設(shè)備,偏壓電阻并且可能包含其他用來(lái)限制帶寬,阻抗匹配和增益控制
2008-11-24 13:37:31
硅振蕩器的優(yōu)點(diǎn)是什么?硅振蕩器有哪些應(yīng)用?硅振蕩器為什么會(huì)取代晶體和陶瓷諧振器?
2021-04-21 06:08:50
圖7所示的緩沖移相振蕩器在2.9kHz處振蕩(理想的頻率為2.76kHz),而且它是在增益為8.33的情況下振蕩(理想的增益為8)。緩沖器避免了各個(gè)RC彼此間的負(fù)載效應(yīng),從而緩沖移相振蕩器可運(yùn)行于更
2015-01-09 11:02:42
有protues仿真西勒振蕩器的嗎?仿真總是不出波
2015-03-31 12:02:17
詳解RC振蕩器通常情況下三點(diǎn)式振蕩器主要用于頻率較高的場(chǎng)合。頻率較低的場(chǎng)合常采用RC 振蕩器。RC 振蕩器的工作原理同三點(diǎn)式振蕩器一樣,都是依靠放大器的正反饋,使電路滿(mǎn)足振蕩的相位條件和振幅條件
2019-06-04 21:18:05
詳解多諧振蕩器多諧振蕩器是一種非正弦波振蕩器,它可以產(chǎn)生連續(xù)的脈沖信號(hào),是應(yīng)用較多的振蕩器。多諧振蕩器可由三極管、門(mén)電路和時(shí)基電路構(gòu)成。下面介紹三極管、門(mén)電路構(gòu)成的多諧振蕩器。1.三極管型多諧振蕩器
2019-06-04 21:16:32
請(qǐng)問(wèn)振蕩器如何生成精確時(shí)鐘源?振蕩的基本原理以及如何在晶體振蕩器中進(jìn)行實(shí)現(xiàn)
2021-04-09 06:25:01
嗨,我有一個(gè)關(guān)于為Spartan 6 FPGA選擇振蕩器的問(wèn)題。我已經(jīng)閱讀了這個(gè)主題:http://forums.xilinx.com/t5/Spartan-Family-FPGA
2019-07-10 09:42:08
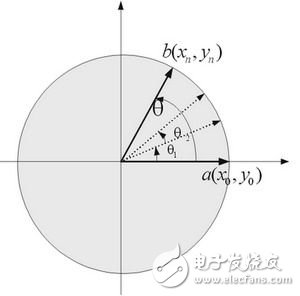
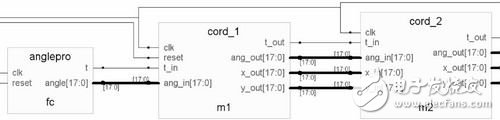
數(shù)控振蕩器的基本實(shí)現(xiàn)原理是什么?如何設(shè)計(jì)一種數(shù)控振蕩器?如何在FPGA器件中利用CORDIC迭代算法產(chǎn)生正余弦信號(hào)?
2021-04-14 07:05:17
請(qǐng)問(wèn)怎么用vhdl語(yǔ)言,基于cordic算法設(shè)計(jì)一個(gè)數(shù)控振蕩器,哪位高手教教我,在下感激不盡!!
2012-04-07 21:28:50
高頻振蕩器電路圖
2019-10-29 09:00:54
RC振蕩器 實(shí)驗(yàn)六
一、實(shí)訓(xùn)任務(wù)1 組裝RC 振蕩器;2 測(cè)量RC 振蕩器。二、實(shí)訓(xùn)目標(biāo)1 學(xué)會(huì)組裝RC 振蕩器電路,理解RC 振蕩器工作原理;2 測(cè)量RC 振蕩器
2010-04-21 15:52:08 54
54
能抑制電源電壓漂移的數(shù)控單穩(wěn)態(tài)多諧振蕩器
2009-03-29 09:23:48 334
334 
數(shù)控單穩(wěn)態(tài)多諧振蕩器
2009-03-29 09:25:03 403
403 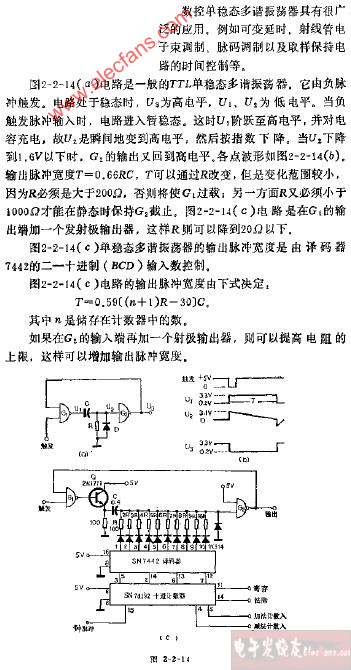
自激振蕩器電路
圖 自激振蕩器電路
圖示出自激振蕩器電路部分。實(shí)驗(yàn)發(fā)現(xiàn)此振蕩器正
2009-07-18 12:09:46 10737
10737 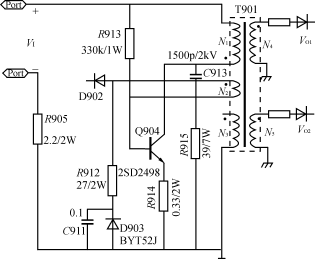
基于FPGA和SRAM的數(shù)控振蕩器的設(shè)計(jì)與實(shí)現(xiàn)
1 引言 數(shù)控振蕩器是數(shù)字通信中調(diào)制解調(diào)單元必不可少的部分,同時(shí)也是各種數(shù)字頻率合成器和數(shù)字信號(hào)發(fā)生器的核心。
2010-01-07 10:35:53 786
786 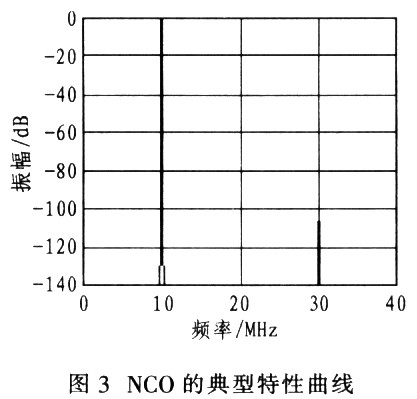
振蕩器,振蕩器是什么意思
振蕩器
振蕩器(英文:oscillator)是一種能量轉(zhuǎn)換裝置——將直流電能轉(zhuǎn)換
2010-03-08 17:41:00 9219
9219 振蕩器,振蕩器的分類(lèi),振蕩器的特性
振蕩器定義振蕩器簡(jiǎn)單地說(shuō)就是一個(gè)頻率源,一般用在鎖相環(huán)中。詳細(xì)說(shuō)就是一個(gè)不需要
2010-03-08 17:46:29 1242
1242 振蕩器,振蕩器的分類(lèi)和原理是什么?
振蕩器定義振蕩器簡(jiǎn)單地說(shuō)就是一個(gè)頻率源,一般用在鎖相環(huán)中。詳細(xì)說(shuō)就是一個(gè)不需要
2010-03-22 14:04:15 18191
18191 正弦波振蕩器,正弦波振蕩器是什么意思
正弦波振蕩器:一種不需外加信號(hào)作用,能夠輸出不同頻率正弦信號(hào)的自激振蕩電路。
自激振蕩的工
2010-03-22 14:09:44 4248
4248 反饋式振蕩器,反饋式振蕩器工作原理分析
反饋式振蕩器的工作原理
1、組成與分類(lèi)
(1) 組成
2010-03-22 14:19:24 2787
2787 壓控振蕩器,壓控振蕩器是什么意思
壓控振蕩器(VCO)
壓控振蕩器(VCO)是指信號(hào)發(fā)生器輸出信號(hào)的頻率由外加信號(hào)電壓控制。VCO的頻
2010-03-22 14:29:57 5142
5142 數(shù)控振蕩器(Numerically Controlled Oscillators,NCOs)是軟件無(wú)線(xiàn)電的重要組成部分和研究?jī)?nèi)容,它廣泛應(yīng)用于DSP中,如通信領(lǐng)域的信號(hào)調(diào)制解調(diào),蜂窩電話(huà)、基站、雷達(dá)系統(tǒng)、數(shù)字電視、GPS
2010-03-24 10:46:58 1999
1999 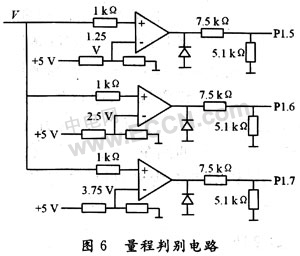
壓控振蕩器(VCO)的定義 控振蕩器工作原理及應(yīng)用
什么叫壓控振蕩器?
指輸出頻率與輸入控制電壓有對(duì)應(yīng)
2010-04-17 08:48:05 5186
5186 
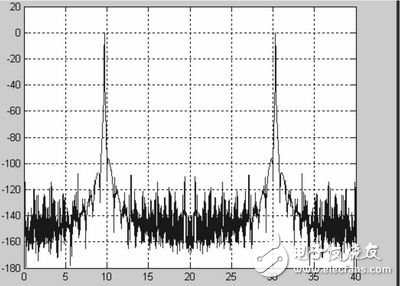
本文通過(guò)分析數(shù)控振蕩器的實(shí)現(xiàn)原理和性能,給出了通過(guò)FPGA來(lái)實(shí)現(xiàn)NCO的具體方法,同時(shí)通過(guò)QUARTUSⅡ中的仿真驗(yàn)證了本設(shè)計(jì)的正確性。
2011-05-09 11:11:07 14048
14048 
開(kāi)拓數(shù)控溫補(bǔ)晶體振蕩器DS4000在GPS中的應(yīng)用
2017-01-24 16:54:24 8
8 本次講座是:PIC10F32X和PIC16F150X系列集成的數(shù)控振蕩器。
2018-06-06 13:46:00 3452
3452 本文主要介紹了新外設(shè)的技巧與訣竅之互補(bǔ)波形發(fā)生器(CWG)和可配置邏輯單元(CLC)及數(shù)控振蕩器(NCO).
2018-06-27 07:25:00 4
4 振蕩器(oscillator)是一種能量轉(zhuǎn)換裝置——將直流電能轉(zhuǎn)換為具有一定頻率的交流電能。其構(gòu)成的電路叫振蕩電路。振蕩器主要可以分成兩種:諧波振蕩器(harmonicoscillator)與弛張振蕩器(relaxationoscillator)。
2019-04-02 16:48:09 30708
30708 正余弦信號(hào)的實(shí)現(xiàn)過(guò)程,給出了在FPGA 中設(shè)計(jì)數(shù)控振蕩器的頂層電路結(jié)構(gòu),并根據(jù)算法特點(diǎn)在設(shè)計(jì)中引入流水線(xiàn)結(jié)構(gòu)設(shè)計(jì)。
2020-08-26 17:21:31 2648
2648 
AD9830:一種正弦查找數(shù)據(jù)表--數(shù)控振蕩器
2021-04-29 16:23:28 8
8 在所有低頻振蕩器配置中,維也納電橋是最容易使用的。它可靠,使用標(biāo)準(zhǔn)元件,提供良好的正弦波,并且相當(dāng)不受設(shè)計(jì)所圍繞的運(yùn)算放大器類(lèi)型的影響。然而,維也納橋可能會(huì)被誤解和過(guò)度簡(jiǎn)化,導(dǎo)致設(shè)計(jì)師感到沮喪。本文介紹了使用維恩橋振蕩器的理論和實(shí)用性,以及如何使電路更穩(wěn)定,更靈活。
2023-01-17 09:09:28 913
913 
電子發(fā)燒友網(wǎng)站提供《基于FPGA的神經(jīng)振蕩器設(shè)計(jì)及優(yōu)化.pdf》資料免費(fèi)下載
2023-11-10 09:39:29 0
0 MEMS振蕩器與傳統(tǒng)振蕩器的比較
2023-12-13 16:14:22 132
132 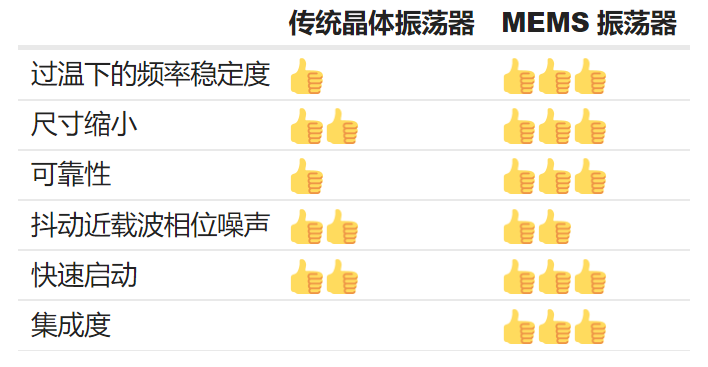
晶體振蕩器與LC振蕩器的區(qū)別? 晶體振蕩器和LC振蕩器是兩種常見(jiàn)的振蕩器結(jié)構(gòu),用于產(chǎn)生穩(wěn)定的振蕩信號(hào)。它們?cè)诮Y(jié)構(gòu)、工作原理、性能等方面存在著一些區(qū)別。本文將從以下幾個(gè)方面對(duì)晶體振蕩器和LC振蕩器進(jìn)行
2023-12-15 14:14:32 619
619 MEMS差分振蕩器與傳統(tǒng)差分振蕩器的比較? MEMS(微機(jī)電系統(tǒng))差分振蕩器是一種基于微納米加工技術(shù)制造的振蕩器,相比于傳統(tǒng)的差分振蕩器,具有獨(dú)特的優(yōu)勢(shì)。傳統(tǒng)差分振蕩器通常采用晶體管或電容等元件
2024-01-26 14:20:52 128
128






 電子發(fā)燒友App
電子發(fā)燒友App



































評(píng)論