摘 要：本文研究了一種運(yùn)用FPGA進(jìn)行數(shù)據(jù)處理的方法，包括：提取輸入數(shù)據(jù)的高log2M個(gè)比特位的數(shù)據(jù)，作為高有效位，根據(jù)預(yù)先設(shè)置的目標(biāo)函數(shù)的計(jì)算表格，查找所述高有效位對(duì)應(yīng)的目標(biāo)函數(shù)值y(n)以及高有效位+1對(duì)應(yīng)的目標(biāo)函數(shù)值y(n+1)；提取輸入數(shù)據(jù)的剩余比特位數(shù)據(jù)，作為低有效位，并將所述低有效位與y(n)和y(n+1)的差值相乘，得到偏移值off(n)，將該偏移值與所述高有效位對(duì)應(yīng)的目標(biāo)函數(shù)值y(n)相加，將計(jì)算結(jié)果作為所述輸入數(shù)據(jù)對(duì)應(yīng)的目標(biāo)函數(shù)值。本方法具有控制簡(jiǎn)單、結(jié)構(gòu)規(guī)則、單運(yùn)算周期、計(jì)算精度較高的特點(diǎn)，適合于FPGA的數(shù)據(jù)處理實(shí)現(xiàn)。

引言
現(xiàn)場(chǎng)可編程門(mén)陣列（FPGA）芯片在許多領(lǐng)域均有廣泛的應(yīng)用，尤其是在無(wú)線通信領(lǐng)域。FPGA具有極強(qiáng)的實(shí)時(shí)性和并行處理能力，這使其對(duì)信號(hào)進(jìn)行實(shí)時(shí)處理成為可能。FPGA內(nèi)部一般都包含邏輯單元（查找表/觸發(fā)器）、存儲(chǔ)單元（BRAM）、乘加單元（MAC）和一些其他的時(shí)鐘、引腳單元等[1-3]。

現(xiàn)代數(shù)字信號(hào)處理的主要發(fā)展趨勢(shì)是：算法結(jié)構(gòu)日趨復(fù)雜，計(jì)算量大，實(shí)時(shí)性要求高，并且包含大量的三角函數(shù)、開(kāi)方、對(duì)數(shù)等復(fù)雜函數(shù)的計(jì)算。但FPGA內(nèi)部的乘加單元并不適合直接進(jìn)行此類函數(shù)的計(jì)算，需要把各種復(fù)雜函數(shù)分解為簡(jiǎn)單的移位、加法和乘法結(jié)構(gòu)，進(jìn)而在FPGA中實(shí)現(xiàn)[4]。

當(dāng)前，在FPGA上實(shí)現(xiàn)三角函數(shù)、開(kāi)方、對(duì)數(shù)等復(fù)雜函數(shù)的計(jì)算，技術(shù)領(lǐng)域最常見(jiàn)的是除法，其次為開(kāi)方和三角函數(shù)，很少涉及對(duì)數(shù)和其他復(fù)雜一些的函數(shù)。而在FPGA具體的實(shí)現(xiàn)上，此類函數(shù)一般采用直接查表法或冪級(jí)數(shù)展開(kāi)法，對(duì)于三角函數(shù)和開(kāi)方的計(jì)算，也會(huì)采用CORDIC的計(jì)算方法，但這三種方法的應(yīng)用都有一定的局限性[4]。

1 現(xiàn)有的FPGA實(shí)現(xiàn)方法
（1）在FPGA上采用直接查表方法，來(lái)實(shí)現(xiàn)函數(shù)的計(jì)算，具有：
優(yōu)點(diǎn)——通用性強(qiáng)、結(jié)構(gòu)簡(jiǎn)單；
缺點(diǎn)——隨著輸入位寬的增加，內(nèi)部存儲(chǔ)量的消耗呈指數(shù)性增長(zhǎng)。
表1給出了不同輸入輸出位寬所需要的存儲(chǔ)單元（BRAM）。

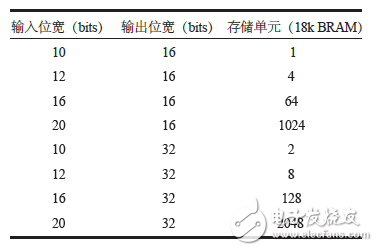
表1 不同輸入輸出位寬所需要的存儲(chǔ)單元

可以看出，輸入輸出位寬較小時(shí)，直接查表法可以滿足實(shí)現(xiàn)要求，但在數(shù)字信號(hào)處理領(lǐng)域，輸入輸出一般都在16bits以上，這時(shí)采用直接查表法就很難滿足實(shí)現(xiàn)需求。

這里以開(kāi)方算法為例進(jìn)行說(shuō)明。采用直接查表法進(jìn)行開(kāi)方計(jì)算有2種方式。

方式一：在完全保證精度的條件下，采用直接查表法。若開(kāi)方為16bits輸入16bits輸出，在完全保證精度的條件下，F(xiàn)PGA就需要存儲(chǔ)216深度的數(shù)據(jù)，需要64塊18k BRAM的存儲(chǔ)空間。而一片中等FPGA一般包含幾十塊到幾百塊的18k BRAM存儲(chǔ)單元，此時(shí)計(jì)算就要用掉大部分的存儲(chǔ)單元，顯然不滿足實(shí)現(xiàn)的資源需求。

方式二：降低精度，減少輸入位寬，采用直接查表法。

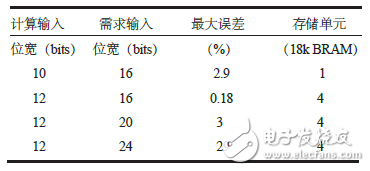
表2 直接查表法開(kāi)方誤差表

可以看出，隨著實(shí)際有效輸入的增加，計(jì)算精度變大，很難滿足計(jì)算的誤差要求。

（2）在FPGA上采用冪級(jí)數(shù)展開(kāi)法計(jì)算函數(shù)。
優(yōu)點(diǎn)——計(jì)算精度可控，多級(jí)展開(kāi)可以達(dá)到較高的計(jì)算精度；
缺點(diǎn)——冪級(jí)數(shù)展開(kāi)法為了達(dá)到較高的精度，需要多級(jí)展開(kāi)，這樣就需要采用較多的資源來(lái)實(shí)現(xiàn)。
以exp為例（0～π/4范圍內(nèi)），采用三角函數(shù)冪級(jí)數(shù)展開(kāi)法：

?

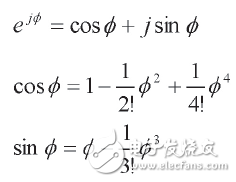
若輸入為16bits，采用冪級(jí)數(shù)展開(kāi)法的計(jì)算框圖如圖1。
從資源方面考慮，三角函數(shù)冪級(jí)數(shù)展開(kāi)法在FPGA中的實(shí)現(xiàn)需要5級(jí)乘法和3級(jí)加法，考慮每級(jí)乘法位寬需要擴(kuò)展，實(shí)際需要FPGA的12個(gè)乘法器
（18bits×18bits）資源。此外從誤差方面考慮，0～π/4范圍內(nèi)，cosΦ的最大誤差為0.046%， sinΦ的最大誤差為0.35%。

?

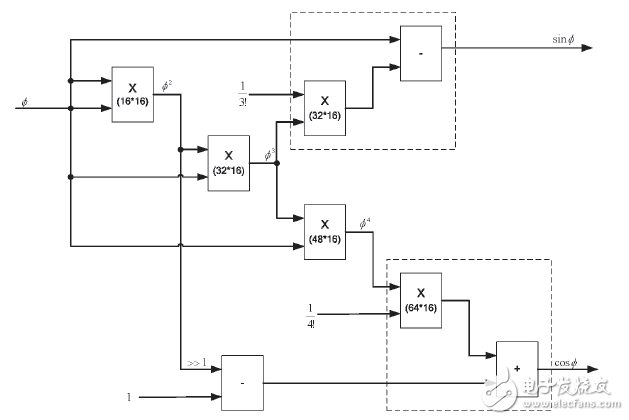
圖 1 冪級(jí)數(shù)展開(kāi)法實(shí)現(xiàn)exp計(jì)算

此外冪級(jí)數(shù)展開(kāi)法的應(yīng)用范圍也比較有限，開(kāi)方、倒數(shù)、對(duì)數(shù)、三角函數(shù)的計(jì)算可以采用冪級(jí)數(shù)展開(kāi)法，但對(duì)于等較復(fù)雜的函數(shù)計(jì)算就不再適合用此方法進(jìn)行計(jì)算。

（3）在FPGA上采用CORDIC法來(lái)實(shí)現(xiàn)函數(shù)的計(jì)算。
優(yōu)點(diǎn)：將復(fù)雜的運(yùn)算分解為簡(jiǎn)單移位、加迭代
運(yùn)算，結(jié)構(gòu)規(guī)則，運(yùn)算周期可以預(yù)測(cè)，比較適合于FPGA實(shí)現(xiàn)；
缺點(diǎn)：一般使用多周期方式，單周期方式資源消耗較高，并且計(jì)算僅限于向量旋轉(zhuǎn)、開(kāi)方等有限的范圍。
采用CORCIC計(jì)算三角函數(shù)，16bits輸入，在多周期條件下需要500個(gè)左右的LUT/FFs，在單周期條件下，需要1000個(gè)左右的LUT/FFs。

2 本文提出的方法
本文在FPGA上采用兩級(jí)方法進(jìn)行函數(shù)計(jì)算：第一級(jí)，直接利用輸入數(shù)據(jù)的高有效位確定計(jì)算結(jié)果的有效范圍；第二級(jí)，直接利用輸入數(shù)據(jù)的低有效位進(jìn)行計(jì)算結(jié)果的誤差調(diào)整。本研究方法充分利用FPGA內(nèi)部的各種邏輯資源、乘加器（或乘法器）資源和BRAM資源：可以根據(jù)FPGA內(nèi)部BRAM資源的大小采用相應(yīng)深度的數(shù)據(jù)表存儲(chǔ)第一級(jí)數(shù)據(jù)的有效范圍；采用FPGA內(nèi)部的乘加器（或乘法器）資源進(jìn)行乘加操作。此方法具有控制簡(jiǎn)單，結(jié)構(gòu)規(guī)則，單運(yùn)算周期，計(jì)算精度較高的特點(diǎn)，適合于FPGA的算法實(shí)現(xiàn)。

此外，采用本研究方法的兩級(jí)計(jì)算的方法，不同函數(shù)的計(jì)算實(shí)現(xiàn)方法一致，只要修改第一級(jí)計(jì)算高有效位數(shù)據(jù)表格中的數(shù)據(jù)，就可以復(fù)用設(shè)計(jì)，有利于資源共享和模塊化實(shí)現(xiàn)。

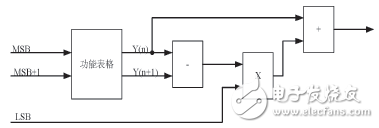
圖2 FPGA兩級(jí)法進(jìn)行函數(shù)的計(jì)算

同現(xiàn)有方案的比較分析：
（1）同直接查表法比較
以開(kāi)方為例進(jìn)行，資源和誤差的列表如表3。可以看出，在資源和誤差方面，本研究方法在FPGA上實(shí)現(xiàn)函數(shù)計(jì)算優(yōu)勢(shì)明顯。此外，F(xiàn)PGA可以通過(guò)增加存儲(chǔ)單元和擴(kuò)展輸出位寬來(lái)進(jìn)一步提高計(jì)算精度。

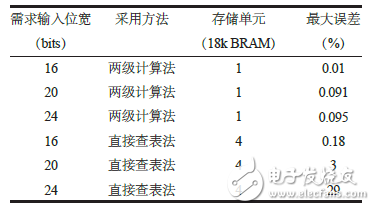
表3 兩級(jí)計(jì)算法開(kāi)方同直接查表法誤差比較表

（2）同冪級(jí)數(shù)展開(kāi)法的比較
首先，本問(wèn)題出的新方法比冪級(jí)數(shù)展開(kāi)法的應(yīng)用范圍更廣泛。其次，在同樣的函數(shù)下，以exp的計(jì)算為例，本文提出的新方法資源更好，誤差更小。在資源方面，F(xiàn)PGA上采用的兩級(jí)計(jì)算方法， 同時(shí)計(jì)算只需要2個(gè)乘法器即可，遠(yuǎn)遠(yuǎn)少于冪級(jí)數(shù)展開(kāi)法的資源消耗；在誤差方面，0～π/4范圍內(nèi)，16bits輸入，cosΦ和sinΦ的最大誤差都小于10-5，因此此方法誤差比冪級(jí)數(shù)展開(kāi)法誤差要小。

（3）同CORDIC方法比較
首先，本文提出的新方法比冪級(jí)數(shù)展開(kāi)法的應(yīng)用范圍更廣泛。其次，在同樣的函數(shù)下，以exp的計(jì)算為例，新方法資源消耗相對(duì)較少，cosΦ和sinΦ同時(shí)計(jì)算只需要300個(gè)左右的LUT/FFs即可。而且，新方法采用的是單運(yùn)算周期模式，運(yùn)算速度更高。