一、CRC簡介
循環冗余校驗(Cyclic Redundancy Check, CRC)是一種根據網絡數據包或電腦文件等數據產生簡短固定位數校驗碼的一種散列函數,主要用來檢測或校驗數據傳輸或者保存后可能出現的錯誤。它是利用除法及余數的原理來作錯誤偵測的。
在數據傳輸過程中,無論傳輸系統的設計再怎么完美,差錯總會存在,這種差錯可能會導致在鏈路上傳輸的一個或者多個幀被破壞(出現比特差錯,0變為1,或者1變為0),從而接受方接收到錯誤的數據。為盡量提高接受方收到數據的正確率,在接收方接收數據之前需要對數據進行差錯檢測,當且僅當檢測的結果為正確時接收方才真正收下數據。檢測的方式有多種,常見的有奇偶校驗、因特網校驗和循環冗余校驗等。
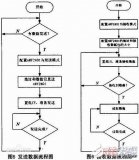
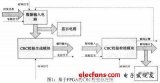
二、CRC硬件計算過程
1.設置CRC寄存器,并給其賦值FFFF(hex)。
2.將數據的第一個8-bit字符與16位CRC寄存器的低8位進行異或,并把結果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB補零,移出并檢查LSB。
4.如果LSB為0,重復第三步;若LSB為1,CRC寄存器與多項式碼相異或。
注意:該步檢查LSB應該是右移前的LSB,即第3步前的LSB。
5.重復第3與第4步直到8次移位全部完成。此時一個8-bit數據處理完畢。
6.重復第2至第5步直到所有數據全部處理完成。7.最終CRC寄存器的內容即為CRC值。
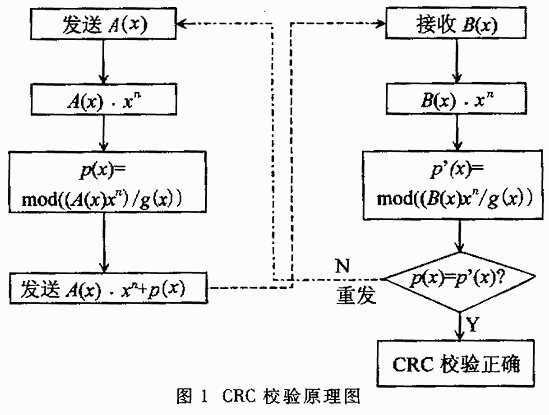
三、循環冗余校驗碼(CRC)的基本原理
在K位信息碼后再拼接R位的校驗碼,整個編碼長度為N位,因此,這種編碼又叫(N,K)碼。對于一個給定的(N,K)碼,可以證明存在一個最高次冪為N-K=R的多項式G(x)。根據G(x)可以生成K位信息的校驗碼,而G(x)叫做這個CRC碼的生成多項式。
校驗碼的具體生成過程為:假設發送信息用信息多項式C(X)表示,將C(x)左移R位,則可表示成C(x)*2R,這樣C(x)的右邊就會空出R位,這就是校驗碼的位置。通過C(x)*2R除以生成多項式G(x)得到的余數就是校驗碼。
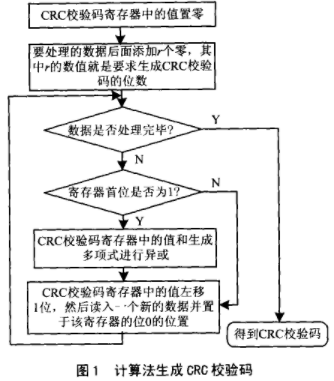
原理思維導圖總結:

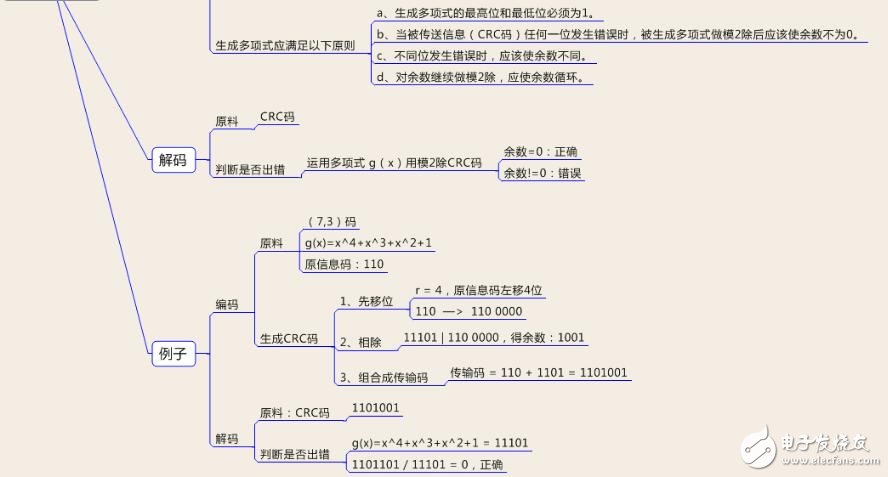
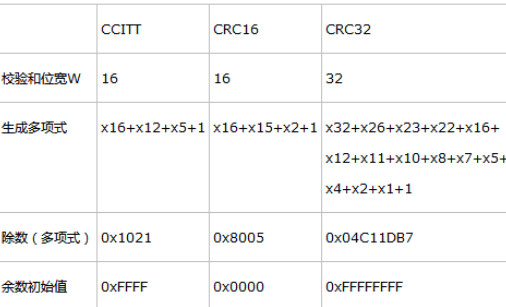
四、通信與網絡中常用的CRC
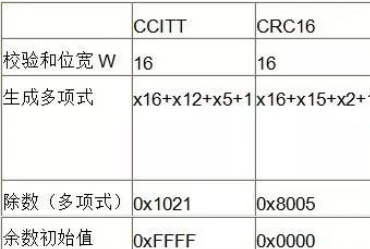
在數據通信與網絡中,通常k相當大,由一千甚至數千數據位構成一幀,而后采用CRC碼產生r位的校驗位。它只能檢測出錯誤,而不能糾正錯誤。一般取r=16,標準的16位生成多項式有CRC-16=x16+x15+x2+1 和 CRC-CCITT=x16+x15+x2+1。
一般情況下,r位生成多項式產生的CRC碼可檢測出所有的雙錯、奇數位錯和突發長度小于等于r的突發錯以及(1-2-(r-1))的突發長度為r+1的突發錯和(1-2-r)的突發長度大于r+1的突發錯。例如,對上述r=16的情況,就能檢測出所有突發長度小于等于16的突發錯以及99.997%的突發長度為17的突發錯和99.998%的突發長度大于17的突發錯。所以CRC碼的檢錯能力還是很強的。這里,突發錯誤是指幾乎是連續發生的一串錯,突發長度就是指從出錯的第一位到出錯的最后一位的長度(但是,中間并不一定每一位都錯)。
【例1】某循環冗余碼(CRC)的生成多項式 G(x)=x3+x2+1,用此生成多項式產生的冗余位,加在信息位后形成 CRC 碼。若發送信息位 1111 和 1100 則它的 CRC 碼分別為_A_和_B_。由于某種原因,使接收端收到了按某種規律可判斷為出錯的 CRC 碼,例如碼字_C_、_D_、和_E_。(1998年試題11)
供選擇的答案:
A:① lllll00 ② 1111101 ③ 1111110 ④ 1111111
B:① 1100100 ② 1100101 ③ 1100110 ④ 1100111
C~E:① 0000000 ② 0001100 ③ 0010111 ⑤ 1000110 ⑥ 1001111 ⑦ 1010001 ⑧ 1011000
解:
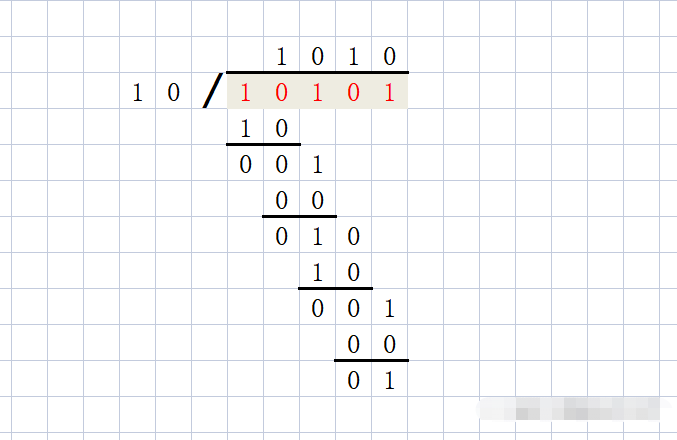
A:G(x)=1101,C(x)=1111 C(x)*23÷G(x)=1111000÷1101=1011余111
得到的CRC碼為1111111
B:G(x)=1101,C(x)=1100 C(x)*23÷G(x)=1100000÷1101=1001余101
得到的CRC碼為1100101
C~E:
分別用G(x)=1101對①~⑧ 作模2除: ① 0000000÷1101 余000 ② 1111101÷1101 余001
③ 0010111÷1101 余000 ④ 0011010÷1101 余000 ⑤ 1000110÷1101 余000
⑥ 1001111÷1101 余100 ⑦ 1010001÷1101 余000 ⑧ 1011000÷1101 余100
所以_C_、_D_和_E_的答案是②、⑥、⑧
【例2】計算機中常用的一種檢錯碼是CRC,即 _A_ 碼。在進行編碼過程中要使用 _B_ 運算。假設使用的生成多項式是 G(X)=X4+X3+X+1, 原始報文為11001010101,則編碼后的報文為 _C_ 。CRC碼 _D_ 的說法是正確的。
在無線電通信中常采用它規定碼字長為7位.并且其中總有且僅有3個“1”。這種碼的編碼效率為_E_。
供選擇的答案:
A:① 水平垂直奇偶校驗 ② 循環求和 ③ 循環冗余 ④正比率
B:① 模2除法 ②定點二進制除法 ③二-十進制除法 ④循環移位法
C:① 1100101010111 ② 110010101010011 ③ 110010101011100 ④ 110010101010101
D:① 可糾正一位差錯 ②可檢測所有偶數位錯
③ 可檢測所有小于校驗位長度的突發錯 ④可檢測所有小于、等于校驗位長度的突發錯
E:① 3/7 ② 4/7 ③ log23/log27 ④ (log235)/7
解:從前面有關CRC的論述中可得出: A:③ 循環冗余 B:① 模2除法
C:G(x)=11011,C(x)=11001010101,C(x)*24÷G(x)=110010101010000÷11011 余0011
得到的CRC碼為② 110010101010011
D:從前面有關通信與網絡中常用的CRC的論述中可得出:④ 可檢測所有小于、等于校驗位長度的突發錯
E:定比碼又叫定重碼,是奇偶校驗的推廣。在定比碼中,奇數或偶數的性質保持不變,然而附加一種限制,每個字中1的總數是固定的。隨用途之不同,定比碼要求的附加校驗位可能多于一個,但較之單一的奇偶校驗將增加更多的檢錯能力。
所謂7中取3定比碼,就是整個碼字長度為7位,其中1的位數固定為3。所有128個7位代碼(0000000~1111111)中只有1的位數固定為3的才是其合法碼字。可以用求組合的公式求出其合法碼字數為:C73=7!/(3!*(7-3)!)=7*6*5/(1*2*3)=35
編碼效率=合法碼字所需位數/碼字總位數=(log235)/7
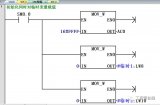
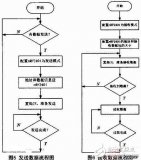
而對于CRC的實現有兩種方式,分別為多項式和查表法。
 電子發燒友App
電子發燒友App








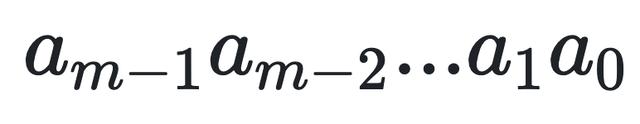




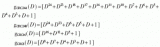
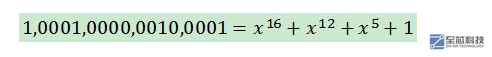


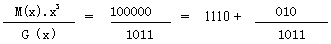











評論