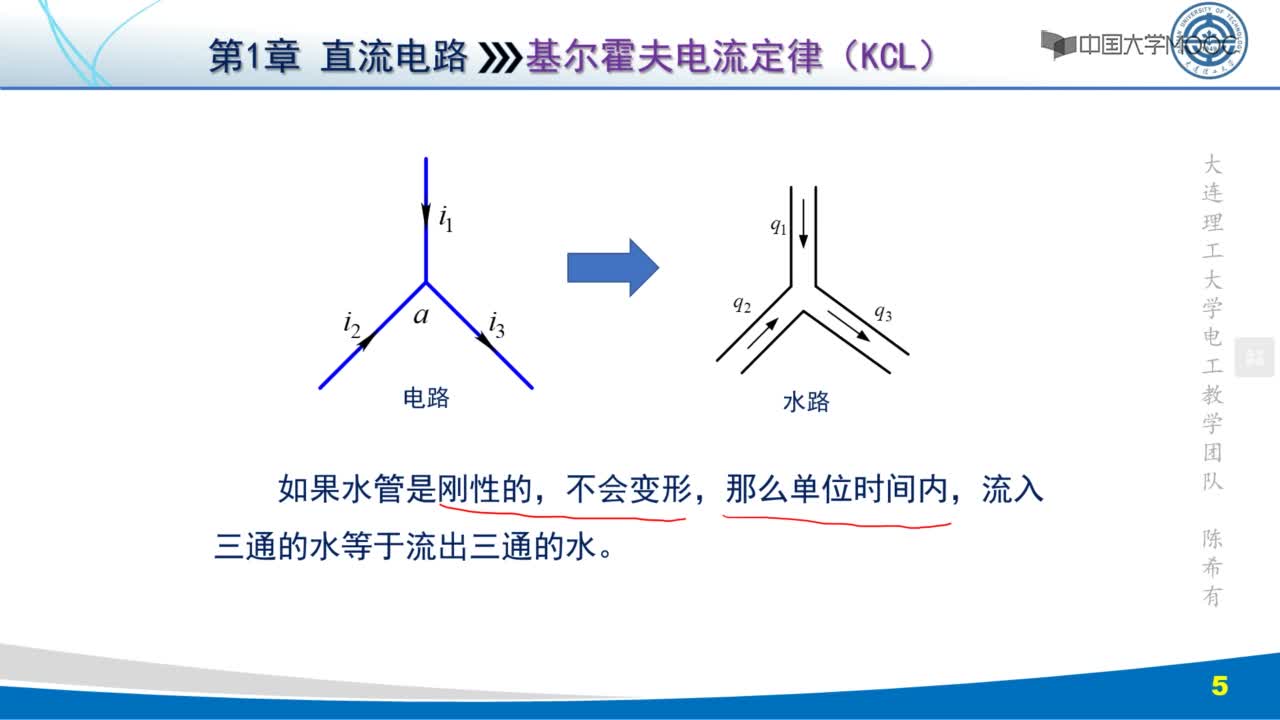
在19世紀(jì)40年代,由于電氣技術(shù)發(fā)展的十分迅速,電路變得愈來愈復(fù)雜。某些電路呈現(xiàn)出網(wǎng)絡(luò)形狀,并且網(wǎng)絡(luò)中還存在一些由3條或3條以上支路形成的交點 (節(jié)點)。這種復(fù)雜電路不是串、并聯(lián)電路的公式所能解決的,剛從德國哥尼斯堡大學(xué)畢業(yè),年僅21歲的基爾霍夫(Gustav Robert Kirchhoff,1824~1887),1845年,在他的第1篇論文中提出了適用于這種網(wǎng)絡(luò)狀電路計算的兩個定律,即著名的基爾霍夫定律。基爾霍夫定律包括基爾霍夫第一定律和基爾霍夫第二定律,其中基爾霍夫第一定律即為基爾霍夫電流定律,簡稱KCL;基爾霍夫第二定律則稱為基爾霍夫電壓定律,簡稱KVL。
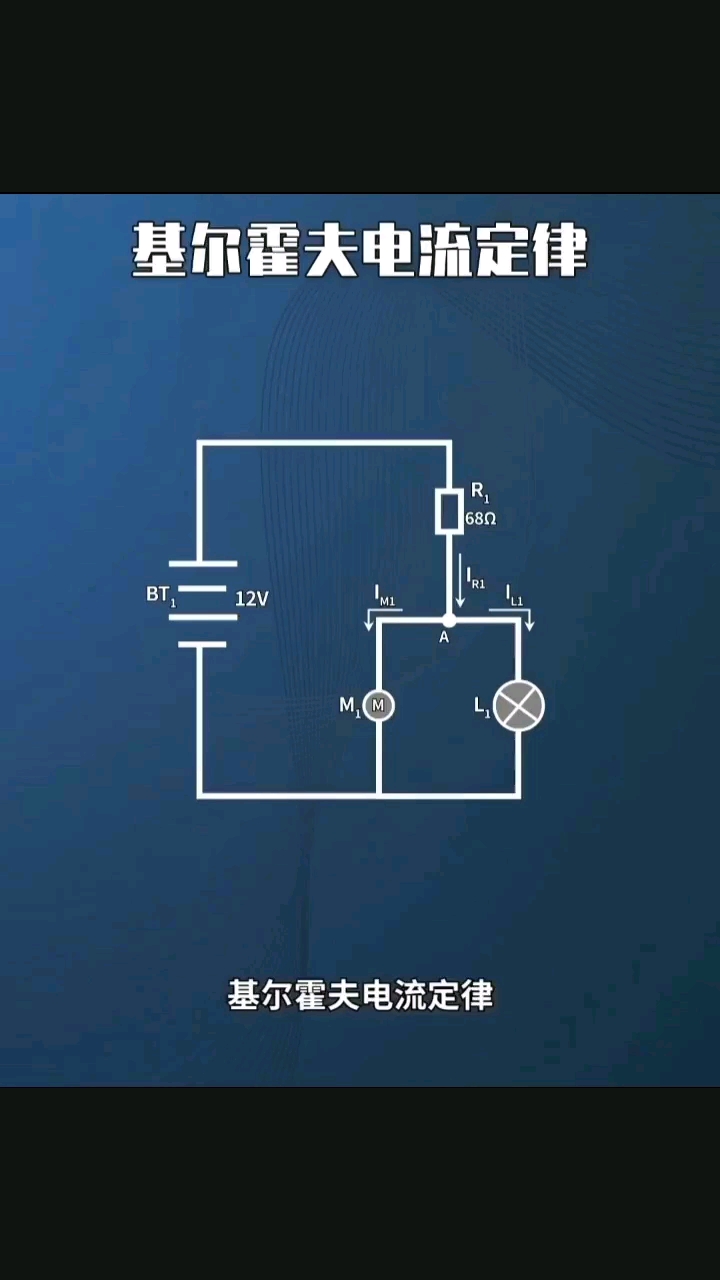
上一篇文章中,我們講到了基爾霍夫第一定律(KCL)即基爾霍夫電流定律,這篇文章,我們將圍繞基爾霍夫第二定律(KVL)即基爾霍夫電壓定律展開探討。
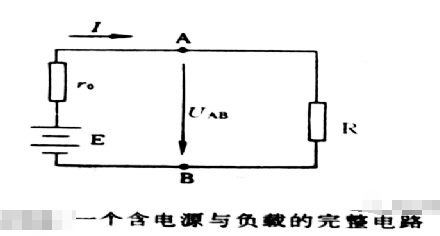
基爾霍夫電壓定律(Kirchhoff laws)是電路中電壓所遵循的基本規(guī)律,是分析和計算較為復(fù)雜電路的基礎(chǔ),內(nèi)容是,在任何一個閉合回路中,各元件上的電壓降的代數(shù)和等于電動勢的代數(shù)和,即從一點出發(fā)繞回路一周回到該點時,各段電壓的代數(shù)和恒等于零,即∑U=0
基爾霍夫電壓定律表明:
沿著閉合回路所有元件兩端的電勢差(電壓)的代數(shù)和等于零。
或者描述為:
沿著閉合回路的所有電動勢的代數(shù)和等于所有電壓降的代數(shù)和。
基爾霍夫電壓定律方程
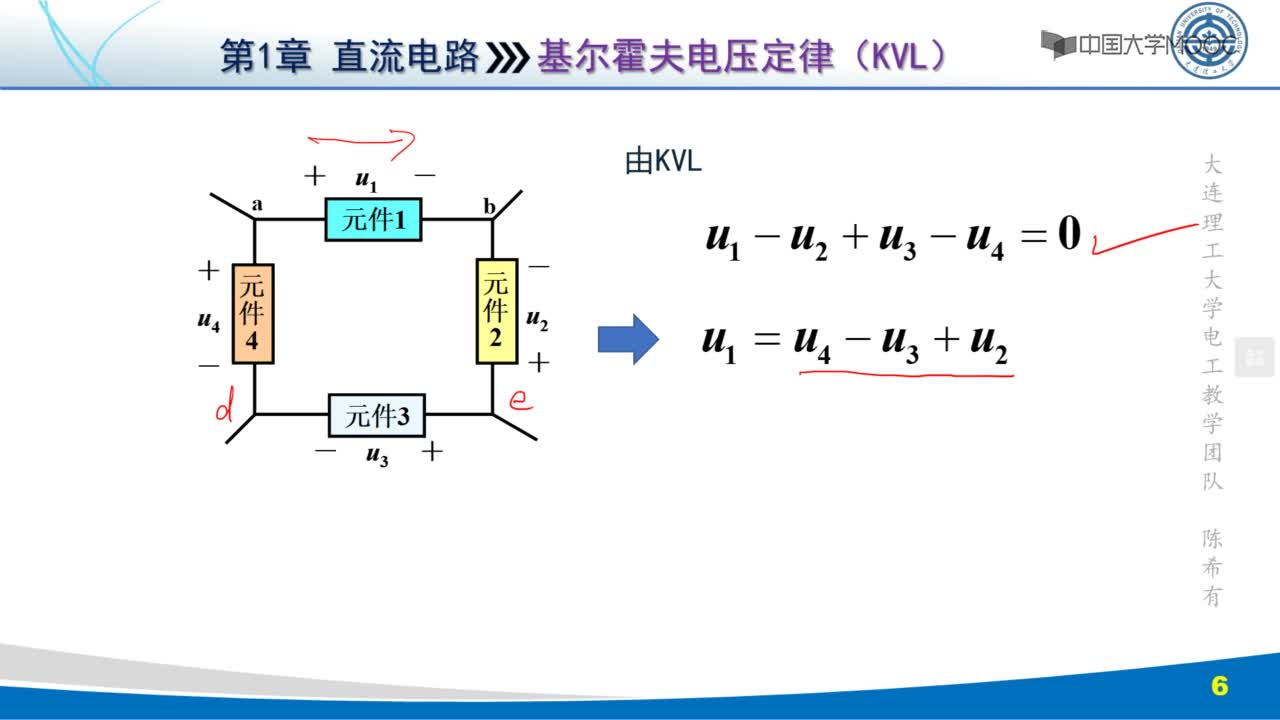
以方程表達(dá),對于電路的任意閉合回路有:
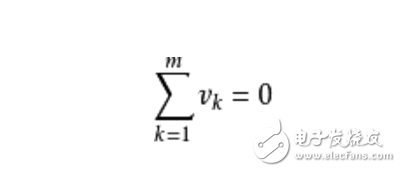
其中,m 是這閉合回路的元件數(shù)目,vk 是元件兩端的電壓,可以是實數(shù)或復(fù)數(shù)。基爾霍夫電壓定律不僅應(yīng)用于閉合回路,也可以把它推廣應(yīng)用于回路的部分電路。
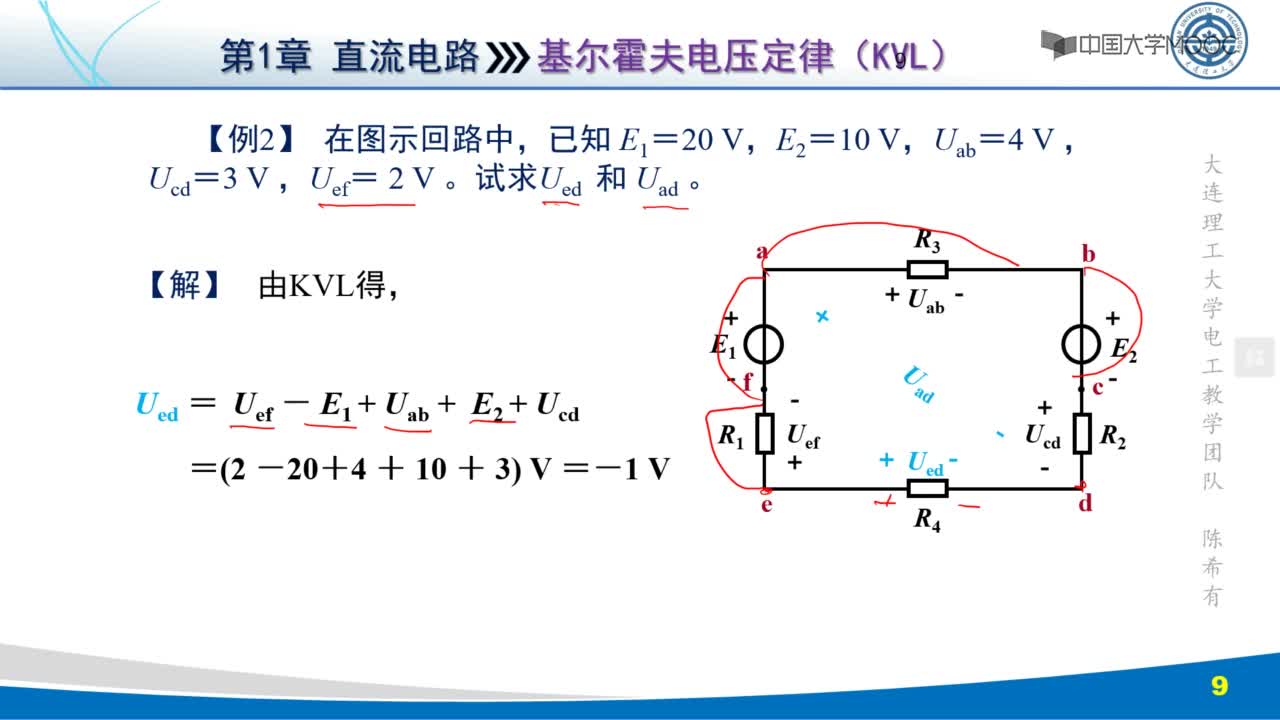
基爾霍夫電壓定律例題
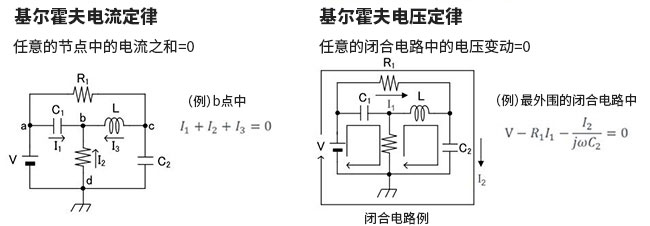
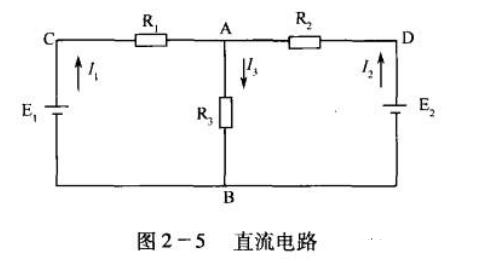
對于任何集總參數(shù)電路的任一回路,在任一時刻,沿該回路全部支路電壓的代數(shù)和等于零,其數(shù)學(xué)表達(dá)式為
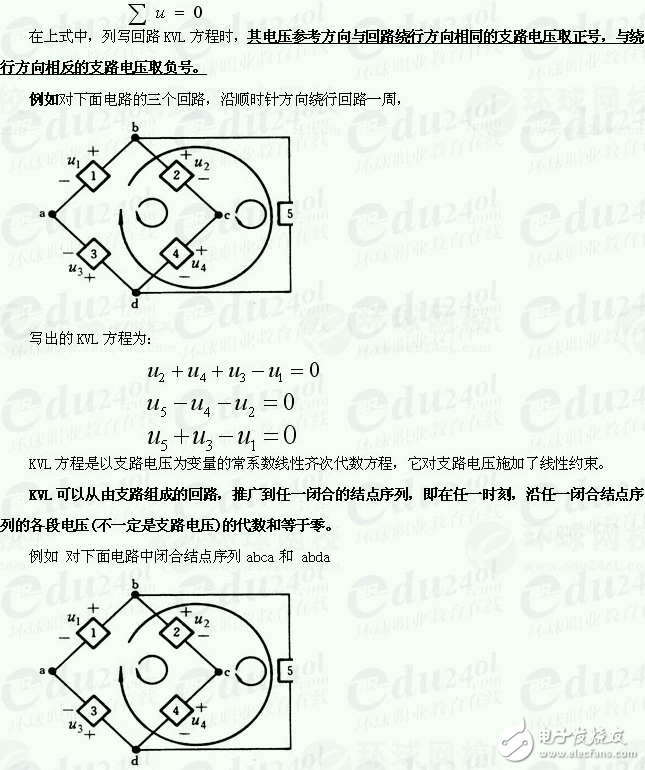
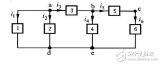
列出的 KVL方程分別為:

由支路組成的回路可以視為閉合結(jié)點序列的特殊情況。沿電路任一閉合路徑(回路或閉合結(jié)點序列)各段電壓代數(shù)和等于零,意味著單位正電荷沿任一閉合路徑移動時能量不能改變,這表明KVL是能量守恒定律的體現(xiàn)。
本節(jié)重點:
(1)基爾霍夫定律是任何集總參數(shù)電路都適用的基本定律。
(2) KCL對電路中任一結(jié)點(或封閉面)的各支路電流施加了線性約束。
(3) KVL對電路中任一回路(或閉合結(jié)點序列)的各支路電壓施加了線性約束。
(4) KCL和KVL適用于任何集總參數(shù)電路、與電路元件的性質(zhì)無關(guān)。
課后習(xí)題:
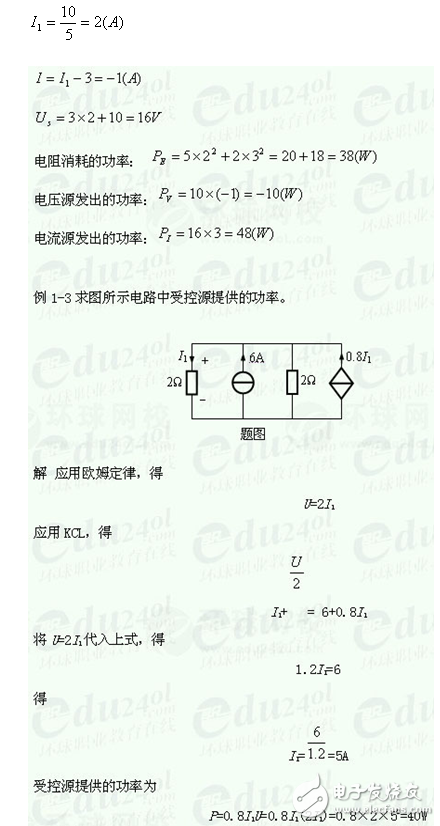
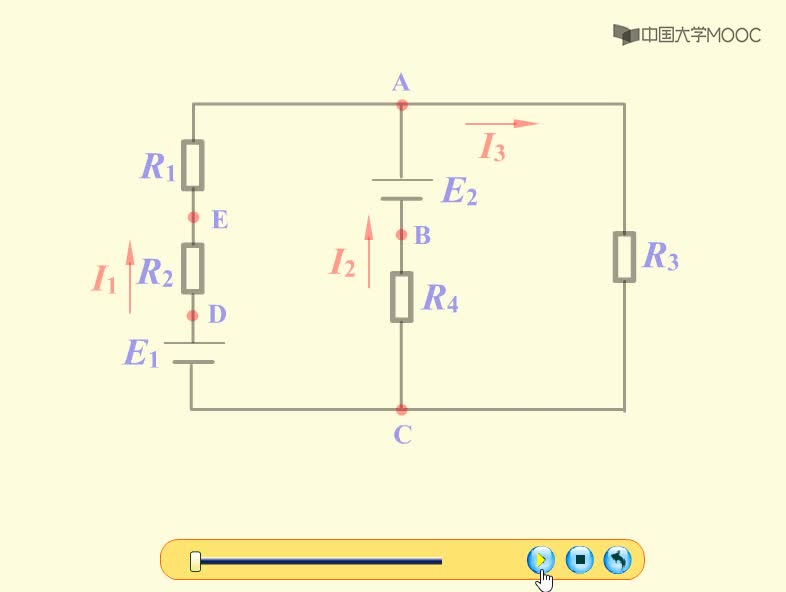
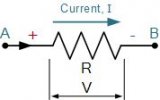
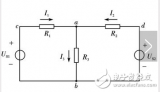
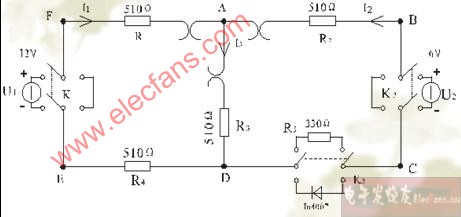
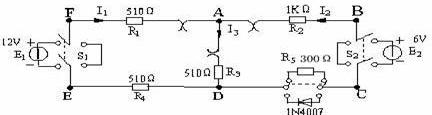
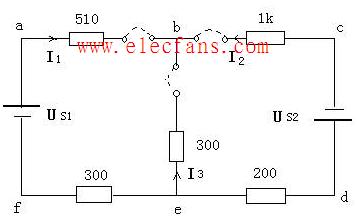
例1-1 求圖中所示個電路中的未知量u,R或i

解:根據(jù)KCL和KVL,考慮到理想電源的基本性質(zhì)和各元件所給出的參考方向,對上圖有:
 電子發(fā)燒友App
電子發(fā)燒友App



































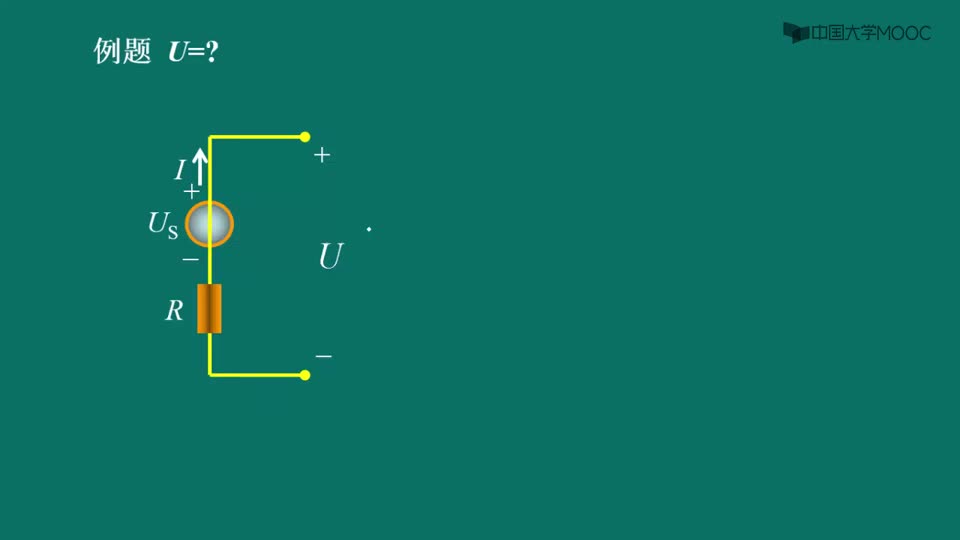






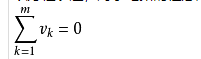
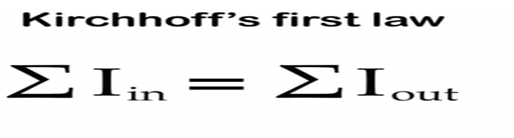













評論