對于微波集成電路來說,微波高通濾波器一般有兩大類設計方法,第一類是用集中或半集中的元件實現,高通濾波器的衰減特性由相應的低通原型的衰減特性經過適當的變換得出。經過變換之后,低通原型電路就成為由串聯電容和并聯電感構成的集中元件高通濾波器。在微波集成電路中,可以用交指電容器或薄膜電容器去實現集中串聯的電容,用并聯的短路短截線或平面螺旋電感去實現集中的并聯電感,它的優點是結構簡單,尺寸較小。但是,在集中參數電路中,這些電感必須靠得很近,這就不可避免地要產生雜散耦合,因此集中元件的高通濾波器很難在微波集成電路中實現。構成高通濾波器的第二類方法是用分布參數來實現,由于傳輸線所固有的多重諧振特性,它必然存在寄生通頻帶,并只能構成帶通特性。這種方法實質上是用寬帶帶通濾波器去充任高通濾波器,即贗高通濾波器。但是對于超寬帶的高通濾波器,這種方法一般結構比較復雜,對工藝要求很高。
本文主要針對第二類方法,利用DGS結構來設計結構簡單,尺寸較小的超寬帶微波高通濾波器。
1 DGS結構簡介
1987年Yablonovitch E和John S提出周期光子帶隙結構(即PBG)。它在接地板上腐蝕出由一定幾何圖形的單元組成的周期性陣列結構,用以改變襯底的有效介電常數分布,從而改變了傳輸線的分布參數模型,在一定頻段內傳播模式也隨之改變,從而具有帶隙特性。PBG開創了在介質板表面和接地板上同時兼顧的設計概念,合理地開發接地板,極大提高了設計靈活性。但是,由于PBG結構模型較復雜,參數也較繁雜,
所以在實踐應用上受到了一定限制。
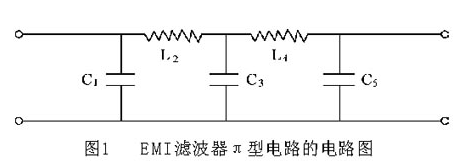
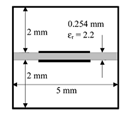
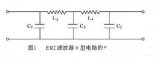
1999年,韓國學者Jong-Im Park,Chul-Soo Kim等人提出一種啞鈴型缺陷地面結構(即DGS),如圖1所示,LC電路如圖2所示。

它主要也是在微帶,共面波導等傳輸線的接地板上腐蝕出具有一定幾何圖形的單元,但DGS可以是周期或非周期的,即一個DGS單元就可以在某頻點上諧振,具有較好的帶隙特性,且等效電路提取也相對容易。
正是由于DGS具有許多獨特的性能,例如單極點低通特性,慢波效應,具有較高特征阻抗等,使得對DGS的研究成為微波電路設計中一個新的研究熱點。近年來對DGS結構的研究層出不窮,在應用方面主要是設計簡單小型化的濾波器,加入DGS改善器件的電器性能,提高天線性能,抑制諧波,減小電路尺寸等。
2 DGS結構對耦合線的影響
兩根微帶線相互隔開距離D,平行排列構成耦合微帶雙線。為簡化問題,令兩條微帶線具有相同參量,具有相同的長度L,寬度W。如圖3所示。

由于在1,4端口上的任意一對輸入電壓U1,U3總可以分解為偶對稱激勵和奇對稱激勵,使U1等于兩分量之和,U3等于兩分量之差。將耦合微帶線分成奇模和偶模的工作狀態后,再分別求得奇偶模參量及它們與耦合參量間的關系。
從定向耦合器的角度來看,2端口為直通端口,3端口為耦合輸出,4端口為隔離端口。

關于耦合線理論本文不再贅述,這里僅就耦合的方向性給出定性的解釋,如圖4所示。當導線1,2中有交變電流i1流過時,3,4線存在耦合過來的能量,此能量既通過電場(以耦合電容表示)又通過磁場(以耦合電感表示)耦合過來。通過Cm的耦合,在傳輸線3,4中引起的電流為ic3,及ic4同時由于i1的交變磁場的作用,在3,4上感應有電流iL。根據電磁感應定律,感應電流iL的方向與i1的方向相反。若能量由1端口輸入,ic3與iL方向相同,所以3端口為耦合輸出。在4端口因為電耦合電流iC4與磁耦合電流iL的作用相反而能量互相抵消,即4端口為隔離端口。
對于均勻介質傳輸TEM波而言,奇模,偶模相速相等,而對于介質非均勻的實際微帶線情況,由于介質基片對奇偶模的電場分布具有不同的影響,使奇偶模兩種情況的有效介電常數或相速不等,嚴格地說,不能搬用由均勻介質情況推出的結論,但是在工程實際中,在有效介電常數取兩者平均值后,仍可近似地采用均勻介質的有關結論。
利用三維電磁仿真軟件Ansoft HFSS建立耦合雙線模型,如圖5所示。其中,D=1 mm,W=1 mm,L=20 mm,基板h=0.254 mm,εr=2.2。

其S參數仿真結果如圖6所示。
當間隔距離D=1mm時,3端口的耦合輸出在DC~15 GHz范圍內不大于-20 dB。要增加兩條微帶線的耦合度,一般要求減小間隔距離D。但是要達到緊耦合,對加工工藝的要求將會非常高。
在耦合微帶線下方加載DGS結構,通過改變耦合微帶線介質的有效介電常數的分布,從而在微帶下方缺陷地面的“槽”將能量耦合過去。加DGS結構的耦合雙線如圖7所示,HFSS模型如圖8所示。


其S13與S14參數仿真結果如圖9,圖10所示。
由仿真結果可以看出,加載DGS結構后,3,4端口的輸出在2~15 GHz范圍內都大于-20 dB,在不改變間隔距離D的情況下,S13平均提高約20 dB。同時注意到S14與S13參數曲線在整個DC~15 GHz頻段內幾乎一樣,即由1,2端口間耦合過來的能量在3,4端口平均分配,即4端口不再是隔離端口,沒有方向性了。
此時,微帶傳播不是TEM波,在加載DGS結構處甚至不是準TEM波。按照左手理論,在DGS結構處的等效介電常數為負值。因此,由于加載DGS結構導致整個介質基板的有效介電常數的分布極不均勻,很難再套用由均勻介質情況推出的奇偶模分析法的結論和公式。可以近似地把DGS結構看作是在接地板上腐蝕出的“槽線”,“槽”與一條微帶線正交耦合,能量通過“槽線”后再耦合到另一條微帶線上,在耦合處向微帶兩側平均傳播能量,即此時還存在兩條微帶線間通過空間的電磁耦合,但是很微弱,“槽”耦合占主導地位。
3 基于DGS的高通濾波器設計
從微帶線的不均勻性角度出發,兩條耦合微帶的1,3端口本身就具有高通特性,如圖6所示的S13,但是由于耦合過于微弱,從而無法形成高通濾波器的通帶。
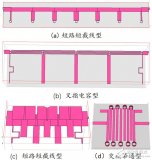
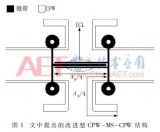
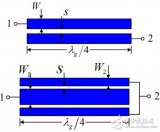
基于前面對于加載DGS結構對耦合線的影響,聯想到可以通過加強兩微帶間的耦合從而使S13形成高通響應,如圖11所示。

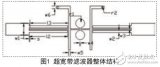
建立HFSS模型如圖12所示。S21參數仿真結果如圖13所示,其等效電路如圖14所示。
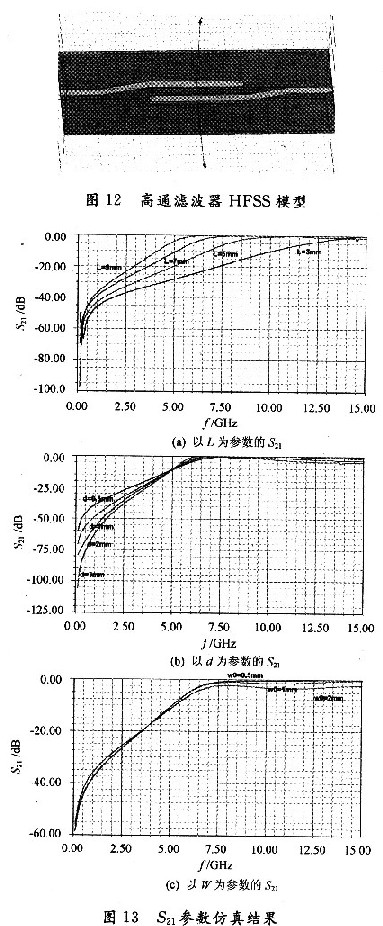

由圖13(a)可以看出長度L影響該高通結構的截止頻率f0,L與f0成反比,L越長,f0越低,且L近似等于1/4截止波長。由圖13(b)可以看出d主要影響高通結構的紋波和矩形系數。d越大,阻帶響應越陡,通帶內紋波越大。同時,對截止頻率有微調作用,但影響不如對紋波和距形系數的影響顯著。由圖13(c)可以看出W0主要影響該高通結構的插入損耗,W0越大,即“槽”越寬,插入損耗越大。
4 測量
使用RT/duroid 5880(基底介電常數εr=2.2,介質厚度h=O.508 mm,銅箔厚度T=O.018 mm)材料制作如圖15所示,截止頻率為7.5 GHz的O~15 GHz超寬帶高通濾波器,其中L=7.8 mm,2d=2 mm,W0=O.5 mm。使用Agilent N5244A矢量網絡分析儀測量結果如圖16所示。仿真結果與試驗結果基本一致,驗證了基于DGS結構的高通濾波器設計的可行性。

5 結語
傳統超寬帶高通濾波器結構較為復雜,對工藝要求較高,且較難實現小型化,利用DGS結構對耦合微帶線的影響,提出結構簡單,易實現小型化的超寬帶高通濾波器,測量結果表明,該結構在O~15 GHz內具有較好的高通濾波特性,在微波混合集成電路,低溫共燒陶瓷(LTCC)電路,多芯片組件(MCM)等領域具有廣泛應用前景。
 電子發燒友App
電子發燒友App











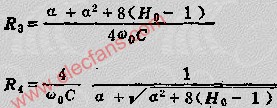
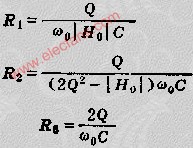












評論