導讀:生活中我們處處面臨最優化的問題,比如,怎么樣一個月減掉的體重最高?怎么樣學習效率最高?怎么樣可以最大化實現個人價值?
顯然,每一個目標都受很多因素的影響,我們稱之為目標函數的最優化。
優化的思路有很多種,比如基于梯度的梯度下降,基于二階梯度的牛頓法,基于近似的二階梯度的擬牛頓法,基于下界函數的最優化,貪婪算法,坐標下降法,將約束條件轉移到目標函數的拉格朗日乘子法等等。
本文我們討論一下基于下界函數的最優化,且將討論的范圍限定為無約束條件的凸優化。
基于下界函數的優化
在有些情況下,我們知道目標函數的表達形式,但因為目標函數形式復雜不方便對變量直接求導。這個時候可以嘗試找到目標函數的一個下界函數,通過對下界函數的優化,來逐步的優化目標函數。
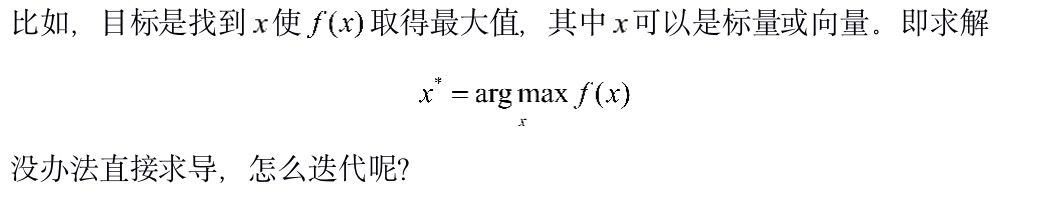



上面的描述性推導很是抽象,下面我們來看兩個具體的例子,EM算法和改進的迭代尺度法。限于篇幅,我們重點推導EM算法,改進的迭代尺度法只是提及一下。
EM算法



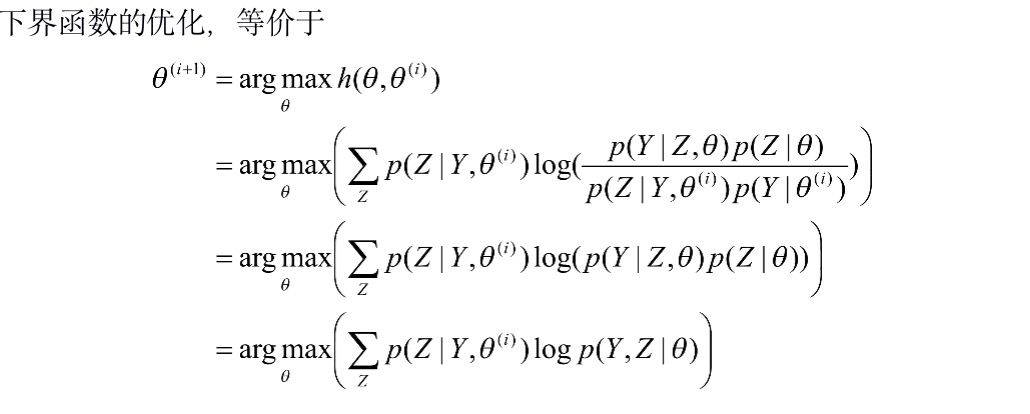
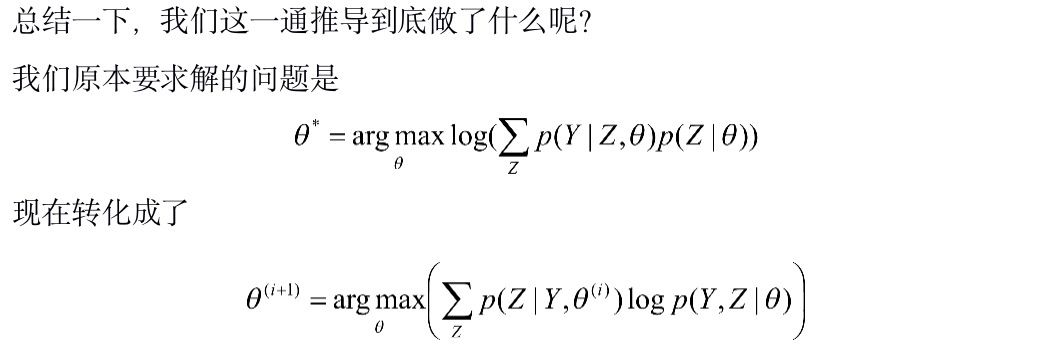



改進迭代算法
概率模型中最大熵模型的訓練,最早用的是通用迭代法GIS(Generalized Iterative Scaling)。GIS的原理很簡單,大致包括以下步驟:
假定初始模型(第0次迭代)為等概率的均勻分布。
用第k次迭代的模型來估算每種信息特征在訓練數據中的分布,如果超過了實際的,就把相應的模型參數變小;反之,將參數變大。
重復步驟2,直到收斂。
GIS算法,本質上就是一種EM算法,原理簡單步驟清晰,但問題是收斂太慢了。Della Pietra兄弟在1996年對GIS進行了改進,提出了IIS(Improved Iterative Scaling)算法。IIS利用log函數的性質,以及指數函數的凸性,對目標函數進行了兩次縮放,來求解下界函數。詳情可參閱李航的《統計學習方法》一書。
小結
本文討論了一下基于下界函數的最優化這樣一種優化思路,希望對大家有所幫助。同時也一如既往地歡迎批評指正,以及大神拍磚。
-
算法
+關注
關注
23文章
4620瀏覽量
93046 -
函數
+關注
關注
3文章
4338瀏覽量
62739
原文標題:優化思路千萬種,基于下界函數的最優化效率如何?
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種基于經優化算法優化過的神經網絡設計FIR濾波器的方法介紹
labview數據的組合排序最優化
粒子群算法城鎮能源優化調度問題
一種求解非線性約束優化全局最優的新方法
一種解決函數優化問題的免疫算法
Matlab最優化方法

一種具有全局快速尋優的多學科協同優化方法

一種小生境灰狼優化算法
一種語義規則為指導的增量優化方法
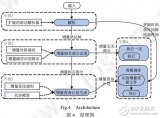
一種改進灰狼優化算法的用于求解約束優化問題
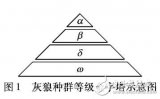




 基于下界函數的最優化這樣一種優化思路
基于下界函數的最優化這樣一種優化思路










評論