網格電流分析是一種用于在電路的任何閉合路徑中找到在環路或網格周圍循環的電流的技術。
雖然基爾霍夫定律為我們提供了基本方法分析任何復雜的電路,通過使用網格電流分析或節點電壓分析,可以通過不同的方法改進這種方法,從而減少所涉及的數學運算網絡涉及這種數學減少可能是一個很大的優勢。
例如,考慮上一節中的電路示例。
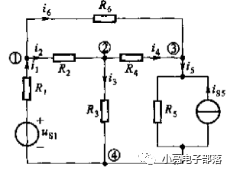
網狀電流分析電路
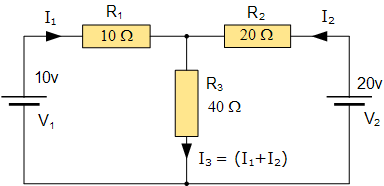
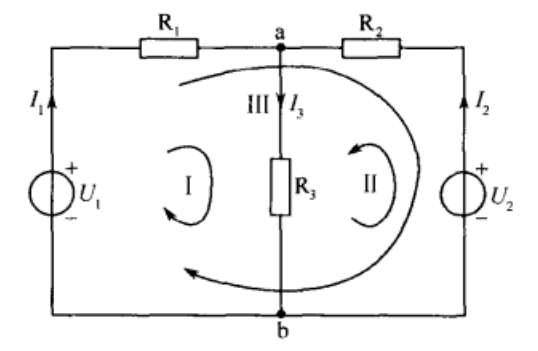
減少數學量的一種簡單方法是使用基爾霍夫電流定律方程分析電路,以確定電流, I 1 和 I 2 流入兩個電阻器。然后,無需計算當前 I 3 ,因為它只是 I 1 和 I <子> 2 。因此,基爾霍夫的第二個電壓定律變為:
等式1: 10 = 50I 1 + 40I 2
公式2: 20 = 40I 1 + 60I 2
因此,已經保存了一行數學計算。
網格電流分析
解決上述電路的一種更簡單的方法是使用網格電流分析或循環分析,有時也稱為Maxwell的循環電流方法。我們需要用循環電流標記每個“閉環”,而不是標記分支電流。
作為一般的經驗法則,只有順時針方向的環路標記,循環電流的目標是覆蓋電路的所有元件至少一次。任何所需的分支電流都可以從適當的環路或網狀電流中找到,如前所述使用Kirchhoff方法。
例如:: i 1 = I 1 ,I <子> 2 = - I 2 和<跨度> I <子> 3 = I 1 -I 2
我們現在以與以前相同的方式編寫Kirchhoff的電壓定律方程來解決它們,但這種方法的優點是它確保了從電路方程獲得的信息是求解電路所需的最小信息,因為信息更通用,并且可以很容易地以矩陣形式存儲。
例如,考慮前一節中的電路。
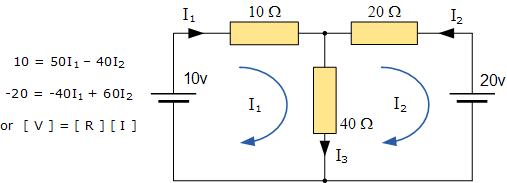
使用單個網格阻抗矩陣 Z 可以非常快速地解決這些方程。主對角線上的每個元素將是“正”,并且是每個網格的總阻抗。其中,每個元素OFF主要對角線將為“零”或“負”,并表示連接所有相應網格的電路元素。
首先我們需要理解在處理矩陣時,對于兩個矩陣的除法與將一個矩陣乘以另一個矩陣的倒數相同,如圖所示。
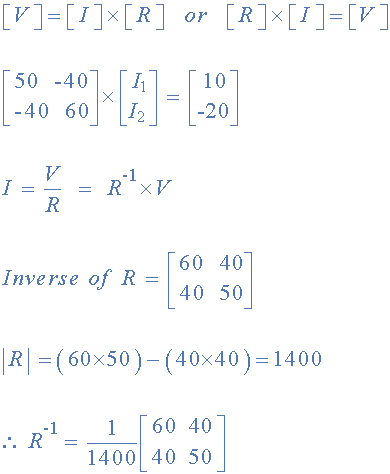
找到 R 的倒數,因為 V / R 與 V x R -1 ,我們現在可以用它來找到兩個循環電流。
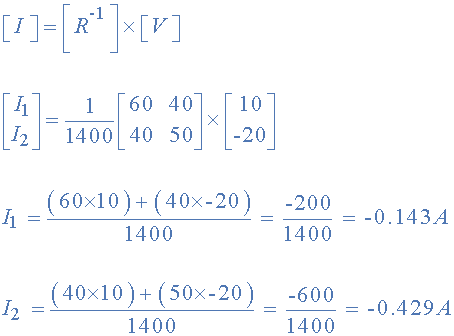
其中:
[V] 給出環路1的總電池電壓,然后是環路2
[I] 表示我們試圖找到的回路電流
[R] 是電阻矩陣
[R -1 ] 是[R]矩陣的反轉
,這使 I 1 為 - 0.143Amps 和 I 2 as -0.429Amps
As: I 3 = I 1 -I 2
因此給出了 I 3 的組合電流as: -0.143 - ( - 0.429)= 0.286Amps
這是 0.286amps 的相同值,我們發現使用Kirchoff的電路定律在上一個教程中。
網格電流分析摘要
電路分析的這種“觀察”方法可能是所有電路分析方法中最好的,具有解決的基本程序網格電流分析方程式如下:
1。用循環電流標記所有內部環路。 (我 1 ,我 2 ,...我 L 等)
2.寫入[ L x 1 ]列矩陣[ V ],給出每個回路中所有電壓源的總和。
3。為電路中的所有電阻寫入[ L x L ]矩陣[ R ],如下所示:
R 11 =第一個循環中的總阻力。
R nn =第N個循環中的總電阻。
R JK =直接將循環J連接到循環K的電阻。
4。寫入矩陣或向量方程 [V] = [R] x [I] 其中 [I] 是要找到的電流列表。
除了使用網格電流分析,我們還可以使用節點分析計算環路周圍的電壓,再次使用基爾霍夫定律減少所需的數學量。在下一個與直流電路理論相關的教程中,我們將研究節點電壓分析。
-
電路
+關注
關注
172文章
5962瀏覽量
172903 -
電流
+關注
關注
40文章
6937瀏覽量
132648
發布評論請先 登錄
相關推薦
無線網狀網絡的路由協議分析
接地電路電流采樣反饋分析
如下電流檢測電路具體是怎么分析的?
電流模式開關電源中斜坡補償電路的分析與設計
藍牙網狀網絡的四大優點分析




 網狀電流分析電路
網狀電流分析電路










評論