材料的電阻率是對電流流動的阻力,某些材料比其他材料更能抵抗電流流動
歐姆法律規(guī)定當(dāng)電壓(V)源之間施加電壓時在這兩個點之間存在電位差的情況下,電路中的兩個點,電流(I)將在它們之間流動。流動的電流量受到存在的電阻(R)的限制。換句話說,電壓會促使電流流動(電荷的移動),但阻力卻是阻力。
我們總是用歐姆測量電阻,其中歐姆用希臘字母Omega表示,Ω。例如:50Ω,10kΩ或4.7MΩ等。導(dǎo)體(例如電線和電纜)通常具有非常低的電阻值(小于0.1Ω),因此我們可以忽略它們,因為我們在電路分析計算中假設(shè)電線為零抵抗性。另一方面,絕緣體(例如塑料或空氣)通常具有非常高的電阻值(大于50MΩ),因此我們也可以忽略它們用于電路分析,因為它們的值太高。
但電氣兩點之間的電阻可取決于許多因素,例如導(dǎo)體長度,其橫截面積,溫度以及制造它的實際材料。例如,假設(shè)我們有一根長度 L 的導(dǎo)線(導(dǎo)體),橫截面積 A 和電阻 R 如圖所示。
單導(dǎo)體

電阻,R這個簡單的導(dǎo)體是其長度L和導(dǎo)體面積的函數(shù).A歐姆定律告訴我們,對于給定的電阻R,流過導(dǎo)體的電流與施加的電壓成比例,即I = V / R.現(xiàn)在假設(shè)我們將兩個相同的導(dǎo)體以串聯(lián)組合連接在一起,如圖所示。
導(dǎo)體長度加倍
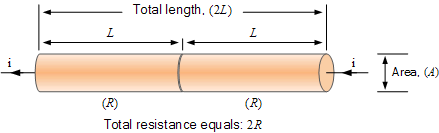
這里通過串聯(lián)組合將兩根導(dǎo)線連接在一起,即端到端,我們有效地將導(dǎo)體的總長度加倍(2L),而橫截面積A仍然是和之前一樣。但是,除了長度加倍之外,我們還將導(dǎo)體的總電阻加倍,得到2R為:1R + 1R = 2R。
因此我們可以看到導(dǎo)體的電阻與其成正比長度,即:RαL。換句話說,我們預(yù)計導(dǎo)體(或?qū)Ь€)的電阻會隨著導(dǎo)體(或?qū)Ь€)的長時間成比例地增大。
還要注意,導(dǎo)體的長度和導(dǎo)體的電阻加倍(2R) ,為了強(qiáng)制相同的電流, i 像以前一樣流過導(dǎo)體,我們需要加倍(增加)施加的電壓,因為現(xiàn)在I =(2V)/(2R)。接下來假設(shè)我們將兩個相同的導(dǎo)體并聯(lián)組合在一起,如圖所示。
將導(dǎo)體面積加倍
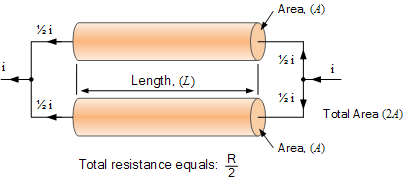
這里通過并聯(lián)組合將兩個導(dǎo)體連接在一起,我們有效地將總面積增加了一倍,而導(dǎo)體長度L保持與原始單導(dǎo)體相同。但是,除了將面積加倍之外,通過將兩個導(dǎo)體并聯(lián)連接在一起,我們有效地將導(dǎo)體的總電阻減半,得到1 / 2R,因為現(xiàn)在每一半的電流都流過每個導(dǎo)體支路。
因此,導(dǎo)體的電阻與其面積成反比,即:R1 /αA或Rα1/ A.換句話說,我們期望導(dǎo)體(或?qū)Ь€)的電阻成比例地越小,其橫截面積就越大。
同樣通過將面積加倍并因此使總電阻減半。導(dǎo)體分支(1 / 2R),對于相同的電流, i 流過并聯(lián)導(dǎo)體支路,如前所述我們只需要一半(減小)所施加的電壓,因為現(xiàn)在I =(1 / 2V)/ (1 / 2R)。
所以希望我們可以看到導(dǎo)體的電阻與導(dǎo)體的長度(L)成正比,即:RαL,與其面積(A),Rα1/ A成反比。因此,我們可以正確地說抵抗是:
抵抗的比例
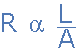
但是除了長度和導(dǎo)體面積之外,我們還期望導(dǎo)體的電阻取決于制造它的實際材料,因為不同的導(dǎo)電材料,銅,銀,鋁等都具有不同的物理和電學(xué)性質(zhì)。因此,我們可以簡單地通過在上面的等式中加上“比例常數(shù)”將上述等式的比例符號(α)轉(zhuǎn)換為等號,給出:
電阻率方程

式中:R是以歐姆為單位的電阻(Ω),L是以米(m)為單位的長度,A是以平方米為單位的面積(m 2 ),其中比例常數(shù)ρ(希臘字母“rho”)被稱為電阻率。
電阻率
特定導(dǎo)體材料的電阻率是材料抵抗通過它的電流強(qiáng)度的量度。該電阻率因子,有時稱為“特定電阻”,使得不同類型導(dǎo)體的電阻能夠根據(jù)它們的物理特性在特定溫度下相互比較,而不考慮它們的長度或橫截面積。因此,ρ的電阻率值越高,電阻越大,反之亦然。
例如,銅等導(dǎo)體的電阻率約為1.72 x 10 -8 歐姆表(或17.2nΩm),而空氣等不良導(dǎo)體(絕緣體)的電阻率可以超過1.5 x 10 14 或150萬億Ωm。
材料例如銅和鋁因其低電阻率而聞名,因此允許電流容易地流過它們,使得這些材料成為制造電線和電纜的理想選擇。銀和金的電阻率值很低,但由于顯而易見的原因,變成電線的成本更高。
那么影響導(dǎo)體電阻(R)的因素可以列為: / p>
制造導(dǎo)體的材料的電阻率(ρ)。
總長度( L)導(dǎo)體。
導(dǎo)體的橫截面積(A)。
導(dǎo)體的溫度。
電阻率示例No1
如果銅的電阻率為20 <,則計算100米2.5mm 2 銅線的總直流電阻sup> o C為1.72 x 10 -8 Ω米。
給出的數(shù)據(jù):20 o C時銅的電阻率為1.72 x 10 -8 ,線圈長度L = 100m,導(dǎo)體的橫截面積為2.5mm 2 ,其面積為:A = 2.5×10 -6 米 2 。
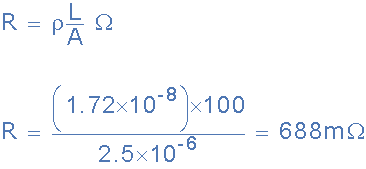
那是688毫米i-ohms或0.688歐姆。
我們之前說過,電阻率是每單位長度和每單位導(dǎo)體橫截面積的電阻,因此表明電阻率ρ具有歐姆表的尺寸,或Ωm因為它是通常寫的。因此,對于特定溫度下的特定材料,其電阻率為:
電阻率,Rho

電氣電導(dǎo)率
雖然電阻(R)和電阻率(或電阻率)ρ都是所用材料的物理性質(zhì),以及其長度表示的物理形狀和尺寸的函數(shù)( L)及其截面積(A),導(dǎo)電率或比電導(dǎo)與電流流過材料的容易程度有關(guān)。
電導(dǎo)(G)是電阻的倒數(shù)(1 / R),電導(dǎo)單位是西門子(S),并給出倒置歐姆符號mho,?。因此,當(dāng)導(dǎo)體具有1西門子(1S)的電導(dǎo)時,其電阻為1歐姆(1Ω)。因此,如果其電阻加倍,則電導(dǎo)減半,反之亦然:西門子= 1 /歐姆,或歐姆= 1 /西門子。
雖然導(dǎo)體電阻給出了它對電阻的影響。在電流流動中,導(dǎo)體的電導(dǎo)表明它允許電流流動的容易程度。因此,銅,鋁或銀等金屬具有非常大的電導(dǎo)值,這意味著它們是良導(dǎo)體。
電導(dǎo)率σ(希臘字母sigma)是電阻率的倒數(shù)。即1 /ρ,以西門子每米(S / m)為單位進(jìn)行測量。由于電導(dǎo)率σ= 1 /ρ,前面的電阻表達(dá)式R可以改寫為:
作為電導(dǎo)率函數(shù)的電阻
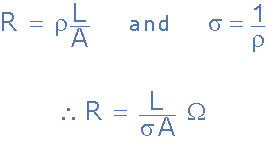
然后我們可以說電導(dǎo)率是導(dǎo)體通過沒有電阻損耗的電流或信號的效率。因此,具有高導(dǎo)電率的材料或?qū)w將具有低電阻率,反之亦然,因為1西門子(S)等于1Ω -1 。因此銅是一種良好的電流導(dǎo)體,其導(dǎo)電率為每米58.14 x 10 6 西門子。
電阻率實例No2
20米電纜長度的橫截面積為1mm 2 ,電阻為5歐姆。計算電纜的電導(dǎo)率。
給出的數(shù)據(jù):直流電阻,R = 5歐姆,電纜長度,L = 20m,導(dǎo)體的橫截面積為1mm 2 給出面積:A = 1 x 10 -6 米 2 。
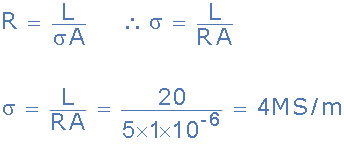
這是每米長度為4兆西門子。
電阻率概述
我們在本教程中已經(jīng)看到電阻率,電阻率是屬性的材料或?qū)w,指示材料傳導(dǎo)電流的程度。我們還看到,導(dǎo)體的電阻(R)不僅取決于制造導(dǎo)體的材料,銅,銀,鋁等,還取決于其物理尺寸。
導(dǎo)體的電阻與其長度(L)成正比,如RαL。因此,它的長度加倍會使其阻力加倍,而將其長度減半會使其阻力減半。此外,導(dǎo)體的電阻與其橫截面積(A)成反比,如Rα1/ A.因此,將其橫截面積加倍會使其阻力減半,而將其橫截面積減半會使其阻力加倍。
我們還了解到導(dǎo)體(或材料)的電阻率(符號:ρ)與制造它的物理性質(zhì)有關(guān),并且因材料而異。例如,銅的電阻率通常為:1.72×10 -8 Ωm。特定材料的電阻率以歐姆 - 米(Ωm)為單位測量,也受溫度的影響。
根據(jù)特定材料的電阻率值,它可以歸類為“導(dǎo)體”,“絕緣體”或“半導(dǎo)體”。請注意,半導(dǎo)體是其導(dǎo)電性取決于添加到材料中的雜質(zhì)的材料。
電阻率在配電系統(tǒng)中也很重要,因為接地系統(tǒng)對電力和配電系統(tǒng)的有效性很大程度上取決于關(guān)于系統(tǒng)地面位置的土壤和土壤材料的電阻率。
傳導(dǎo)是以電流形式給予自由電子運動的名稱。電導(dǎo)率,σ是電阻率的倒數(shù)。即1 /ρ,單位為西門子每米,S / m。電導(dǎo)率范圍從零(對于完美的絕緣體)到無窮大(對于完美的導(dǎo)體)。因此,超導(dǎo)體具有無限電導(dǎo)和幾乎零歐姆電阻。
-
電阻
+關(guān)注
關(guān)注
87文章
5592瀏覽量
173862 -
電流
+關(guān)注
關(guān)注
40文章
7079瀏覽量
133603 -
電導(dǎo)率
+關(guān)注
關(guān)注
1文章
247瀏覽量
14194
發(fā)布評論請先 登錄
相關(guān)推薦
電阻率對電路性能的影響分析
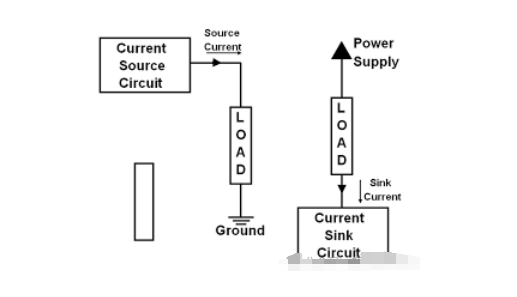
運算放大器與高速DAC的接口,第2部分:電流流出型DACs
運算放大器與高速DAC的接口,第1部分:電流流入型DAC
霍爾電流檢測芯片檢測多大電流
關(guān)于動力學(xué)方程能否用matlab進(jìn)行傅里葉變換的問題。
左行繞組和右行繞組有何區(qū)別
拉電流和灌電流的區(qū)別是什么 拉電流和灌電流哪個大些
電阻阻隔的是電壓還是電流,電阻阻擋的電流會流失嗎
電流流的是正電荷還是負(fù)電荷
可以把光電二極管的電流流入OPA365芯片的輸出端嗎?
電阻和開關(guān)并聯(lián)時電流走哪一個
靜電計怎么測電阻率?
逆變器絕緣抵抗和殘余電流不同,發(fā)生較大故障




















評論