電阻也可以用于交流電源,其中消耗的電壓,電流和功率以rms值給出
在前面的教程中,我們已經研究了電阻器,它們的連接和使用歐姆定律計算與它們相關的電壓,電流和功率。在所有情況下,電壓和電流都被假定為具有恒定的極性,流量和方向,換句話說,直流或DC。
但是還有另一種稱為交流電或AC的電源,其電壓從正到負切換,并且隨時間再次返回,并且其電流相對于電壓來回振蕩。 AC電源的振蕩形狀遵循“正弦波”的數學形式,其通常稱為正弦波形。因此,正弦電壓可定義為 V(t)= V max sinωt。
在交流電路中使用純電阻時,其值可忽略不計電感或電容的相同原理,歐姆定律的相同原理,電壓,電流和功率的電路規則(甚至基爾霍夫定律)適用于直流電阻電路,這次唯一的區別在于使用瞬時“峰值到達” -peak“或”rms“數量。
使用AC交流電壓和電流時,通常只使用”rms“值以避免混淆。 AC波形的均方根或“均方根”值是AC波形的有效值或DC值。用于定義AC電壓源的示意符號也是“波浪”線的示意符號,而不是DC的電池符號,如下所示。
DC和AC電源的符號表示
電阻器是“無源”器件,即它們不會產生或消耗任何電能,而是將電能轉換為熱。在直流電路中,電阻器中電壓與電流的線性比稱為其電阻。但是,在交流電路中,電壓與電流之比取決于電源的頻率和相位差或相位角(φ)。因此,當在交流電路中使用電阻時,術語阻抗,符號Z是常用的,我們可以說直流電阻=交流阻抗, R = Z
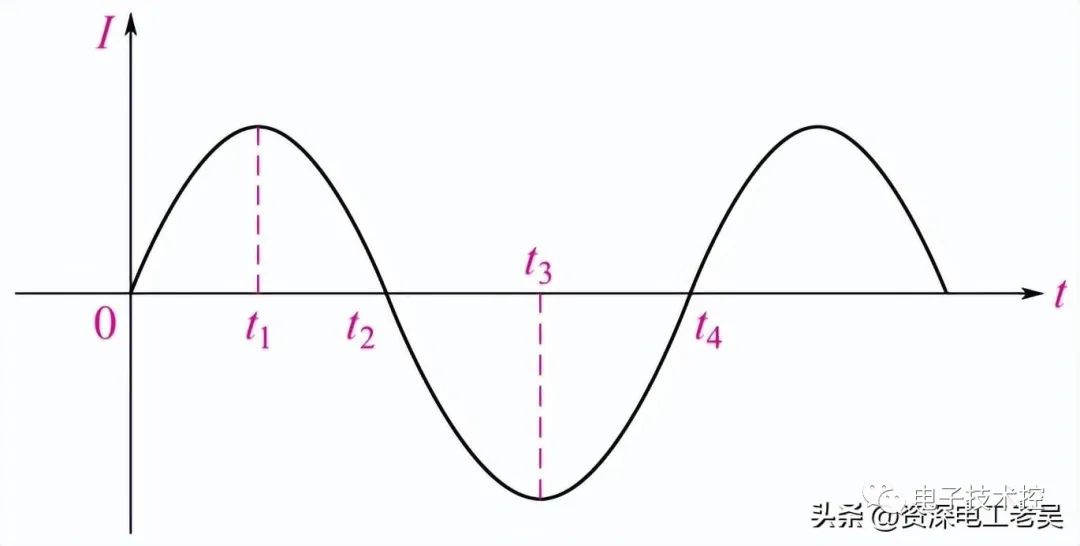
對于交流電路中的電阻,流過它們的電流方向對電阻的行為沒有影響,因此隨著電壓的上升和下降會上升和下降。電流和電壓達到最大值,從零降至最小值并達到最小值。即,它們同時上升和下降,并被稱為“同相”,如下所示。
VI相位關系和矢量圖
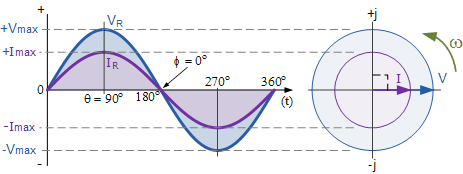
我們可以看到,在水平軸的任何一點,瞬時電壓和電流是同相的,因為電流和電壓同時達到它們的最大值,它們的相角θ是0 o 。然后,可以比較這些電壓和電流的瞬時值,簡單地通過使用歐姆定律給出電阻的歐姆值。在下面考慮由交流電源和電阻組成的電路。
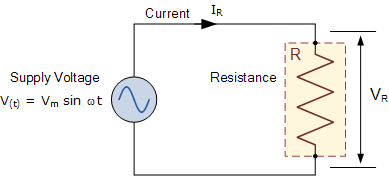
電阻上的瞬時電壓, V R 等于電源電壓 V t ,給出如下:

電阻器中流過的瞬時電流將是:

當電阻兩端的電壓為 V R = IR 時,上面電阻上的瞬時電壓也可以給出為:

在純電阻串聯交流電路中,電阻上的所有電壓降可以加在一起找到總電路電壓,因為所有電壓彼此同相。同樣,在純電阻并聯交流電路中,所有單個支路電流可以加在一起,以找到總電路電流,因為所有支路電流都是同相的。
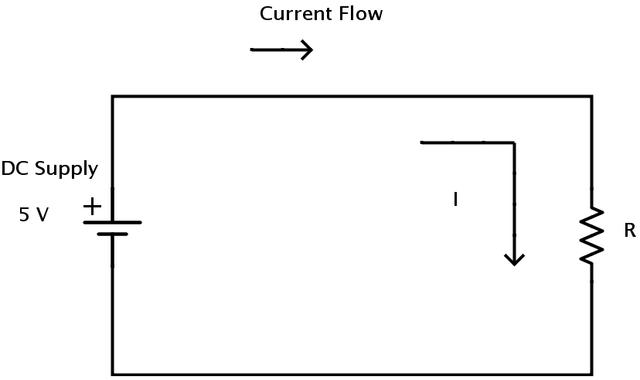
因為交流電阻器電路中電壓和電流之間的相位角φ為零,然后電路的功率因數給出為 cos0 o = 1.0 。任何時刻電路中的功率都可以通過乘以該時刻的電壓和電流來找到。
然后電路消耗的功率(P)為 P = Vrmslcos Φ以瓦特為單位。但由于純電阻電路中的 cos(Φ)= 1 ,所消耗的功率簡單地給出,與<歐姆定律相同, P = Vrmsl 。
然后,這給出了“功率”波形,并且在下面顯示為一系列正脈沖,因為當電壓和電流都處于它們的正半周時,所得的功率為正。當電壓和電流都為負時,兩個負值的乘積給出正功率脈沖。
純電阻中的功率波形
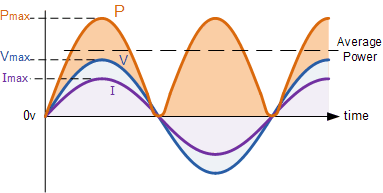
然后,從交流有效值電源饋送的純阻性負載中的功耗與連接到直流電源的電阻相同,并給出如下:
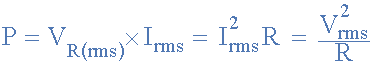
其中:
P 是瓦特的平均功率
V rms 是電壓有效值電源電壓
I rms 是以安培為單位的均方根電源電流
R 是電阻器的電阻,單位為歐姆(Ω) - 實際應為Z表示阻抗
最大值 Imax 的交流電產生的加熱效果與相同值的直流電流不同。為了將AC加熱效果與等效DC進行比較,必須使用rms值。任何電阻加熱元件,如電爐,烤面包機,水壺,電熨斗,熱水器等都可以歸類為電阻交流電路,我們在交流電路中使用電阻來加熱我們的房屋和水。
交流電阻器電路示例No1
1000瓦(1kW)的加熱元件連接到250V AC電源電壓。計算元件在高溫時的阻抗(交流電阻)和從電源獲取的電流量。
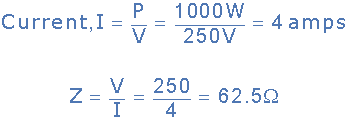
交流電路中的電阻示例No2
計算連接在240V電源上的100Ω電阻元件所消耗的功率。
由于只有一個元件連接到電源,電阻器,然后 V R = V S
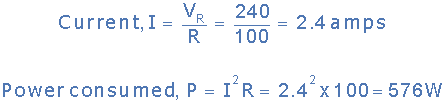
>>
然后總結一下,在純歐姆交流電阻中,電流和電壓都被稱為“同相”,因為它們之間沒有相位差。流過電阻器的電流與其兩端的電壓成正比,在AC電路中這種線性關系稱為阻抗。與直流電路一樣,在交流電路中使用電阻器來計算電阻器電壓,電流和功率時,可以使用歐姆定律。
-
電阻器
+關注
關注
21文章
3938瀏覽量
63051 -
交流電路
+關注
關注
0文章
186瀏覽量
29082
發布評論請先 登錄
相關推薦








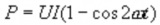
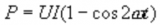











評論