我思故我在

AI背后的神秘公式

近代哲學奠基人，偉大的笛卡爾說出“我思故我在”時，上帝震驚了。

第一個被賦予公民身份的機器人Sophia（索菲婭）被問到：你怎么知道自己是機器人？Sophia的回答是：你怎么知道自己是人類？

機器人會反駁了，這到底是新世紀的福音，還是人類的轉折？

AI（人工智能）已經不再是完全被動地向人類表述世界，而開始主觀性地表達意見。

Google自動駕駛汽車的操縱系統，G-mail對垃圾郵件的處理，MIT主導的人類“寫字”系統，以及最新的SIRI智能語音助手平臺，還有挑戰人類最后智慧堡壘的AlphaGo系統，都已經開始了“深度學習”暴風雨式革命。

這幾年，機器智能向“我思故我在”這個哲學命題步步逼近，一只神秘之手躲在后面操縱，它就是貝葉斯公式。

當科學在證明自己對世界的客觀認知時，貝葉斯公式卻融入了人類的主觀性。

1

“不科學”的貝葉斯-拉普拉斯公式

貝葉斯定理是18世紀英國數學家托馬斯·貝葉斯提出的概率理論。

該定理源于他生前為解決一個“逆概”問題寫的一篇文章，在貝葉斯寫這篇文章之前，人們已經能夠計算“正向概率”，如“假設袋子里面有P只螃蟹，Q只蜘蛛，你伸手進去摸一把，摸到螃蟹的概率是多大”。但反過來看：“如果我們事先并不知道袋子里面螃蟹和蜘蛛的比例，而是閉著眼睛摸出一只（或好幾只）螃蟹，那么我們可以就此對袋子里面的螃蟹和蜘蛛的比例作出什么樣的推測。”這個問題就是逆向概率問題。

這個研究看起來似乎簡單而平淡無奇，直到他死后的兩年才于1763年發表。它的數學原理很容易理解，就像一個迷信星座的HR，如果你碰到一個處女座的應聘者，你會推斷那個人多半是一個追求完美的人。這就是說，當你不能準確知悉某個事物本質時，你可以依靠經驗去判斷其本質屬性的概率。與其他統計學方法不同，貝葉斯方法建立在主觀判斷的基礎上，讓人感覺不科學，這也是它200多年來不為科學家們待見的原因。

除了貝葉斯，1774年，法國數學家拉普拉斯也非常“不科學”地發現了貝葉斯公式。這位創立了大名鼎鼎的諦聽神獸拉普拉斯獸的科學家，給出了我們現在所用的貝葉斯公式的表達：

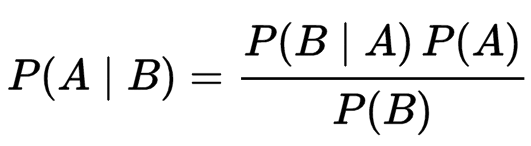
該公式表示在B事件發生的條件下A事件發生的條件概率，等于A事件發生條件下B事件發生的條件概率乘以A事件的概率，再除以B事件發生的概率。公式中，P(A）也叫做先驗概率，P(A/B)叫做后驗概率。

像微積分公式的全稱是“牛頓-萊布尼茨公式”一樣，貝葉斯公式至少應被稱為“貝葉斯-拉普拉斯公式”才科學。

2

今天天氣怎樣？

貝葉斯公式是這樣工作的

貝葉斯定理并不好懂，它到底是如何為人民服務的？

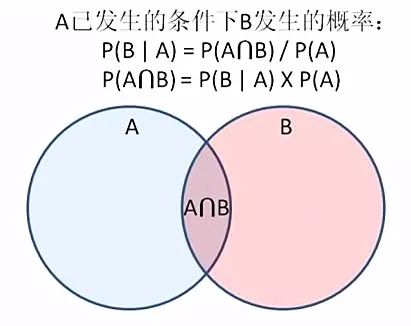
對于貝葉斯定理，參照上面的公式，首先要了解各個概率所對應的事件。

P(A|B)是在B發生的情況下A發生的概率；

P(A)是A發生的概率；

P(B|A)是在A發生的情況下B發生的概率；

P(B)是B發生的概率。

就知道你沒看懂……那我還是舉個經常用到的例子吧！

老板良心發現放假10天，小編約定帥哥去爬山，希望玩到人約黃昏后占點便宜，然而天公不作美，一大早天空多云。

這可怎么辦？60%的雨天的早上是多云的。帥哥說，不玩了吧。

小編當然不甘心，勸說帥哥：

1、多云不見得會下雨，大約30%日子早上是多云的！

2、深圳天氣平均一個月才會3天下雨，10%的概率而已。

帥哥并不是繡花枕頭，非常科學地用“貝葉斯公式”計算：

用“雨”來代表今天下雨，“云”來代表早上多云。

當早上多云時，當天會下雨的可能性是P(雨|云)。

P(雨|云) = P(雨)·P(云|雨) /P(云)

P(雨) 是今天下雨的概率 = 10%

P(云|雨) 是在下雨天早上有云的概率 = 60%

P(云) 早上多云的概率 = 30%

那么，貝葉斯定理的答案就出來了

P(雨|云) =0.1×0.6/0.3=0.20

帥哥毫無表情地說：今天下雨的概率是20%，可以去爬山。

小編看著美得不食人間煙火的帥哥，怯生生地問：你真的是人嗎？

帥哥毫無表情地回答：我不是人，我是阿爾法狼。

3

貝葉斯公式如何逐步取得人類信任

今天的貝葉斯理論開始遍布一切。從物理學到癌癥研究，從生態學到心理學。

物理學家提出了量子機器的貝葉斯解釋，以及貝葉斯捍衛了弦和多重宇宙理論。

哲學家主張作為一個整體的科學可以被視為一個貝葉斯過程。

貝葉斯定理就快成像“熱力學第二定律”一樣放之四海皆準了。

特別是在IT界，AI大腦的思考和決策過程，被更多工程師設計成一個貝葉斯程序。

但貝葉斯誕生以來命途多舛，長期以來因為表面的不科學，并沒有得到主流學界認可。

其實在日常生活中，我們也常使用貝葉斯公式進行決策。比如我們到河邊釣魚，根本就看不清楚河里哪里有魚或者沒魚，似乎只能隨機選擇，但實際上我們會根據貝葉斯方法，利用以往積累經驗找一個回水灣區開始垂釣。這就是我們根據先驗知識進行主觀判斷，在釣過以后對這個地方有了更多了解，然后再進行選擇。所以，在我們認識事物不全面的情況下，貝葉斯方法是一種非常理性且科學的方法。

貝葉斯公式得到主流科學界的認可，主要因為兩件事：

1、《聯邦黨人文集》作者揭密

1788年，《聯邦黨人文集》匿名出版，作者漢密爾頓和麥迪遜寫作風格幾乎一致。兩個人都逝世后，要找出每一篇文章的作者極其困難，哈佛大學通過對詞匯的貝葉斯研究方法最終找出了每一篇的文章作者，研究方法在統計學界引發震動，被禁錮了200年的貝葉斯公式從魔盒里被釋放出來。

2、美國天蝎號核潛艇搜救

1968年5月，美國海軍天蝎號核潛艇在大西洋亞速海海域失蹤。軍方通過各種技術手段調查無果，最后不得不求助于數學家John Craven，John Craven提出的方案使用了貝葉斯公式，他召集了數學、潛艇、海事搜救等各個領域的專家，一邊擲骰子一邊通過貝葉斯公式一一排除小概率發生意外事故的搜索區域。

2014年初馬航MH370航班失聯后，科學家想到第一個方法就是利用貝葉斯定理開始區域搜索，這個時候，貝葉斯公式已經名滿天下了。

4

語音識別

貝葉斯公式開始展示“神跡”

科大訊飛因為語音識別成為千億級市值公司，首先得感謝貝葉斯公式和馬爾科夫鏈。

自然語音處理一直是科學家面臨的最大難題，在計算機語言處理領域，近幾年引入了貝葉斯公式和馬爾科夫鏈才有了長足進步（這里不詳細介紹馬爾科夫鏈）。

文字翻譯尚可理解，但語音涉及各種動態語法，機器怎么知道你在說什么鳥語？

但當你在現場看到機器翻譯的準確性，會感嘆這簡直就是“神跡”，比大部分現場翻譯要強得多。一旦出現條件概率，貝葉斯總能挺身而出。我們用P(f|e)區別于以上的P(A|B)來解釋語音識別功能。

統計機器翻譯的問題可以描述為：給定一個句子e，它可能的外文翻譯f中哪個是最靠譜的。即我們需要計算：P(f|e)。

P(f|e) ∝ P(f) * P(e|f)

這個式子的右端很容易解釋：那些先驗概率較高，并且更可能生成句子e的外文句子f將會勝出。我們只需簡單統計就可以得出任意一個外文句子f的出現概率。然而 P(e|f)卻不是那么好求的，給定一個候選的外文局子f，它生成（或對應）句子e的概率是多大？我們需要定義什么叫“對應”，這里需要用到一個分詞對齊的平行語料庫。率先成功利用數學方法解決自然語言處理問題的是賈里尼克，他把語音識別簡化為用貝葉斯公式處理的數學問題成功開辟了一條全新的問題解決路徑。

隨著大量數據輸入模型進行迭代，隨著計算能力的不斷提高、大數據技術的發展，貝葉斯公式巨大的實用價值愈發體現出來。

語音識別僅僅只是貝葉斯公式運用的一個例子，其實貝葉斯定理的思想已經滲透到AI的方方面面。

5

貝葉斯網絡

AI智慧的“蜂群效應”

單個語音模型的建立讓我們看到了貝葉斯定理解決問題的能力，但貝葉斯網絡的拓展讓我們隱約感覺到了AI背后“天網”的恐怖。

人類相對簡單的問題已經解決得差不多了，剩下的都非常復雜。

龍卷風的形成，2的50次方可能的最小參數值比對。癌癥致病基因，2的100次方種可能的基因圖譜。星系起源，2的350次方種可能的星云數據處理。大腦運作機制，2的1000次可能的意識量子流。

面對這樣數理級的運算，科學家別無選擇，必須從可能的法則中選擇一些可以信任的，并以此為基礎建立理論模型。貝葉斯公式正好以嚴謹的數學形式幫他們實現了這一點。科學家把所有假設與已有知識、觀測數據一起代入貝葉斯公式，就能得到明確的概率值。而要破譯某種現象的成因網絡，只需將公式本身也結成網絡，即貝葉斯網絡，接下來只需要向這個模型代入觀測數據，通過網絡節點間的貝葉斯公式重新計算出概率值。為每個新數據、每個連接重復這種計算，直到形成一個網絡圖，讓任意兩個原因之間的連接都得到精確的概率值為止。人類認知的缺陷越大，貝葉斯網絡展示的力量越讓人震撼。

但這還不是最可怕的，這里我們要引入“蜂群效應”，一只個體蜜蜂，基本上沒有智力，但當它們組建成一個蜂群時，就會爆發出一種整體智力，擁有記憶能力，能制造出巧奪天工的蜂巢。貝葉斯網絡的每一個節點就像一只蜜蜂，這種群體的連接不僅生動，而且非常嚴謹，一旦這個群體達到一定數量級別，有沒有可能產生整體智慧？這不僅是哲學家需要思考的問題，生命學家需要討論的問題，AI圈的科學家也應該直接去面對。

今天一場轟轟烈烈的“貝葉斯革命”正在AI界發生：貝葉斯公式已經滲入到工程師的骨子里，分類算法也成為主流算法。在很多人眼中，貝葉斯定理就是AI進化論的基石。

結

封殺這個公式，

AI智商將為零？

AI人工智能第一課，都是從貝葉斯定理開始。因為大數據、人工智能和自然語言處理中都大量用到貝葉斯公式。

我們無法預測到貝葉斯公式與計算機結合的真正威力，因為一切才剛剛開始。

貝葉斯公式與AI的結合，這到底是一場科學的革命，還是一場理念的革命？到底是生產方式的革命，還是人類在革自己的命？

當年人類科學家總結出客觀的貝葉斯公式，而AI卻利用這個公式給自己注射主觀基因，兩者顛倒，在未來到底會演繹怎樣的相愛相殺故事？

如果真的到了決戰的一天，人類到底該如何給自己留一把殺手锏？是否應該像NSA在算法里留下后門一樣，抽離出這個公式，讓AI無法“我思故我在”。

這似乎有點杞人憂天了，縱觀整個社會，現在不用太擔心AI像人一樣思考，最應該擔心人類已經失去了思考。