在設(shè)計(jì)反激變壓器時經(jīng)常會采用 Ap 法來選擇磁芯,然而常見的 Ap 法公式算出的結(jié)果并不準(zhǔn)確(普遍偏小)通常還要結(jié)合經(jīng)驗(yàn)法。從原理講 Ap 法并無不妥,造成偏差的原因就在于波形系數(shù)設(shè)置的不正確,下面將用公式逐一的推出和驗(yàn)證反激變壓器的正確的波形系數(shù)。
變壓器主要是由磁芯和導(dǎo)線繞組構(gòu)成,正常工作的變壓器要同時滿足磁芯不飽和導(dǎo)線不過流的要求,Ap 法正是基于這個原理設(shè)置了一個最大的 Bm 和 Jm計(jì)算出最小的 Ae 和 Aw(Ae 磁芯截面積、Aw 窗口面積),Ap=Ae×Aw 單位是面積乘積。這里的波形系數(shù)也是由兩部分組成的(內(nèi)部有關(guān)聯(lián))一個是從磁的角度一個從電的角度。
從磁的角度由法拉第電磁感應(yīng)開始
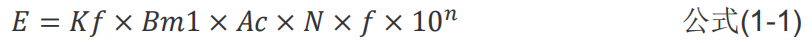
公式后面的10^n跟所選取的單位有關(guān),常數(shù) Kf 在正弦波工作時選取 4.44,方波時取 4,對于正弦波或方波默認(rèn)的占空比為0.5。
對于反激變壓器作用在磁芯上的只有正半周的占空比為 0.5 的方波(脈沖矩形波),公式(1-1)中的 Bm1=Bm/2(Bm 表示峰峰值),將公式變換一下得
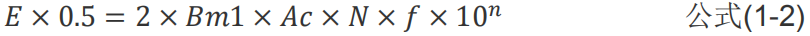
等式前面的 0.5 表占空比,后面的2×Bm1表峰值,公式再變換得
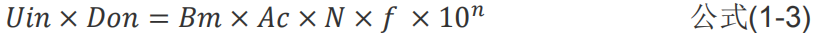
從公式(1-3)可以看出對于反擊變壓器這種脈沖矩形波,波形系數(shù)中是沒有4.44 或 1.11 的。
公式(1-3)屬臨界狀態(tài)方程更準(zhǔn)確的表達(dá)式如下式
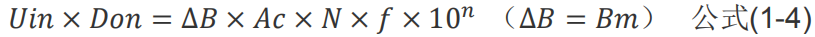
法拉第電磁感應(yīng)只跟變化的磁通有關(guān),在臨界模式剛好變化的磁通=峰值磁通既△B=Bm。
連續(xù)模式下的磁通先參看下圖
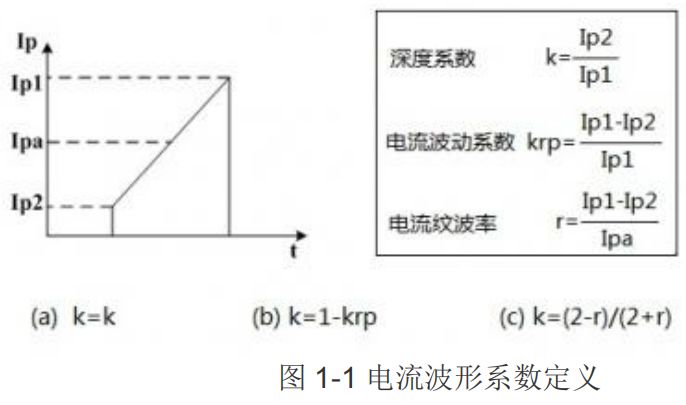
電和磁是緊密關(guān)聯(lián)的,有電就有磁有磁既有電(這里的電指“凈”電,對于正激變壓器“凈電”=輸入電流-輸出電流),通過觀察電流的情況既可得知磁通的變化情況。通過圖 1-1 可知變化的電流△I=(1-k)×Ipk,則可推出變化的磁通△B=(1-k)×Bm,將△B代入公式(1-4)
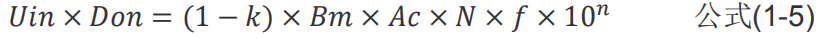
公式(1-5)中的 1-k 既為磁的波形系數(shù),對于臨界和斷續(xù)模式 k=0。
從電的角度考慮的是導(dǎo)線損耗和發(fā)熱,對于磁關(guān)注的是最大磁通密度 Bm,對于電關(guān)注的是有效電流值,導(dǎo)線的峰值電流并不是主要問題。
關(guān)于有效值波形系數(shù)的幾種表達(dá)式如下圖
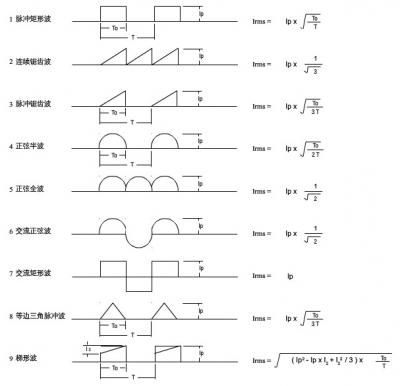
對于反激變壓器斷續(xù)、臨界模式是波形(3)脈沖鋸齒波,連續(xù)模式是波形(9)梯形波。電流密度和電流有效值的關(guān)系公式如下:

式中ku表示窗口系數(shù)一般取0.3-0.5。
公式(2-1)中的電流有效值是初級+次級總的有效值,有些公式直接代用了 圖1-2的波形 (9)梯形波公式并不合適,總的電流有效值計(jì)算起來有些麻煩所以用一種等效法來簡化這個問題。
等效法參考下圖:
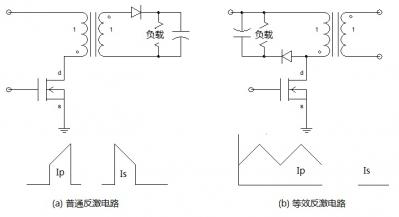
圖1-3 等效法分析有效電流
圖1-3中為簡化分析將匝比設(shè)為1:1,圖(a)為正常的反激工作方式,在Ton時刻初級線圈導(dǎo)通初級電流為Ip,在Toff時刻次級線圈導(dǎo)通次級電流為Is,在整個T周期初、次級線圈是輪流導(dǎo)通的導(dǎo)線利用率是0.5。圖(b)與圖(a)在功率處理上是完全相同的,由于電流都在初級所以分析起來比較容易。圖(b)與圖(a)的區(qū)別就是沒有隔離功能,次級線圈雖然沒有電流但占了窗口面積,導(dǎo)線利用率也是0.5。電流的波形系數(shù)將由圖(b)推導(dǎo)出來。
一種比較簡單的方法是采用中心電流法,如下圖
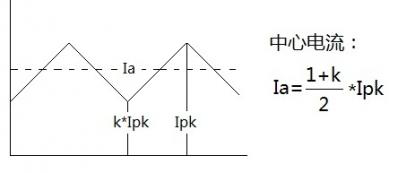
圖1-4 中心電流Ia
用中心電流Ia來代替有效電流,方程如下

前面提到反激電路或其等效電路導(dǎo)線利用率只有0.5,所以公式中要多乘以0.5 將中心電流方程代入公式(2-2)得
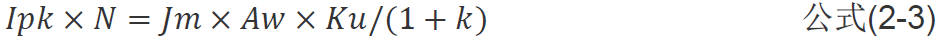
公式(2-3)中的 (1+k)/2既為電流的波形系數(shù)。
將公式(2-3)電方程和公式(1-5)磁方程等式兩邊分別相乘,
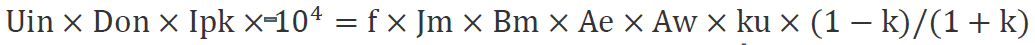
整理得
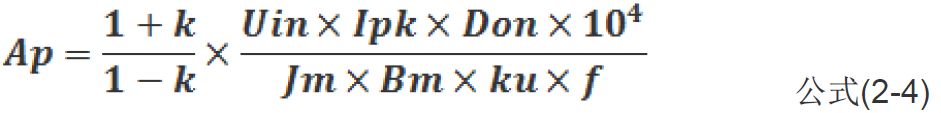
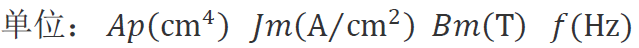
公式(2-4)為簡潔版AP算法,(1+k)/(1-k)既為波形系數(shù)。
圖1-4的電流是鋸齒波,其有效值的表達(dá)式為

代入深度系數(shù)k
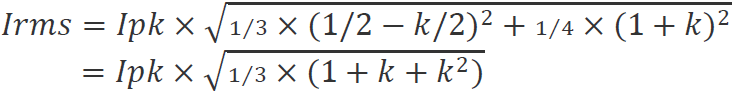
導(dǎo)線的發(fā)熱功耗為
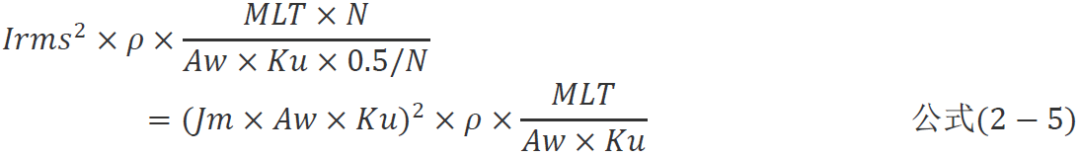
代入電流有效值并化簡得
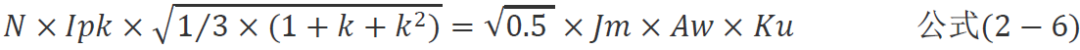
最終推出比較精確的AP算法為:
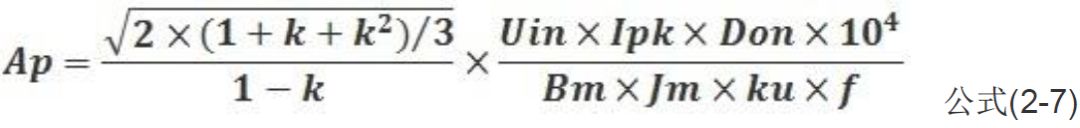
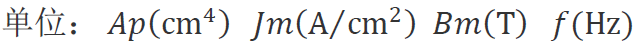
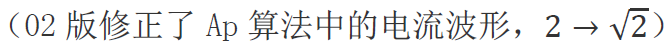
下面的是直接由初級導(dǎo)線功耗+次級導(dǎo)線功耗=總導(dǎo)線功耗推導(dǎo)的電流波形系數(shù)。
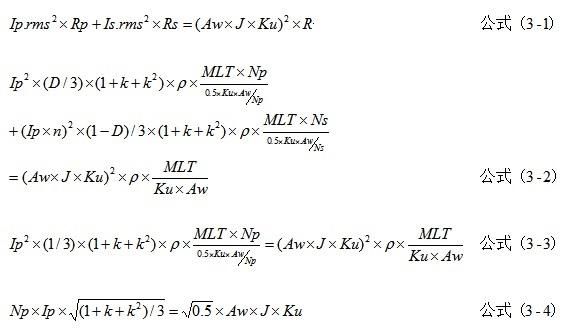
推導(dǎo)結(jié)果同等效法一致,證明匝比不影響等效法。
-
AP
+關(guān)注
關(guān)注
0文章
107瀏覽量
49435 -
磁芯
+關(guān)注
關(guān)注
6文章
295瀏覽量
23458
原文標(biāo)題:【推導(dǎo)】Ap法計(jì)算磁芯變壓器!
文章出處:【微信號:dianyuankaifa,微信公眾號:電源研發(fā)精英圈】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦





 Ap法計(jì)算磁芯變壓器
Ap法計(jì)算磁芯變壓器











評論