這一篇文章聊一聊CRC算法的硬件電路實現：串行電路和并行電路。

下面的內容還是IC君的朋友文武寫的，IC君稍微做了優化排版和少量的編輯工作提升大家的閱讀體驗。

1

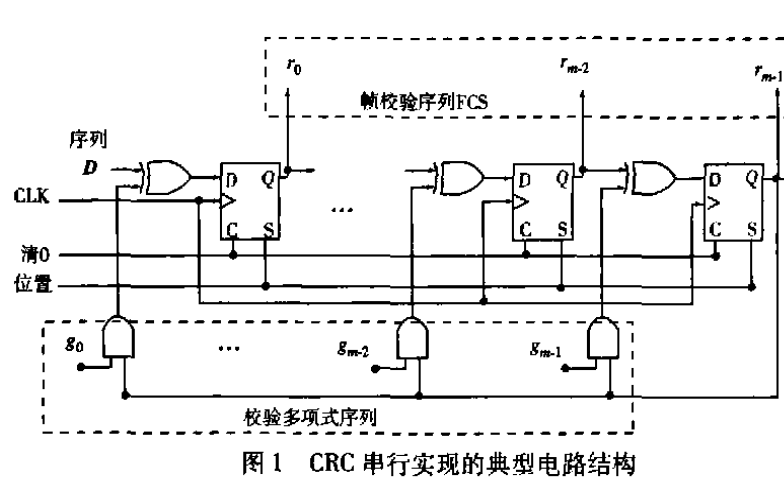
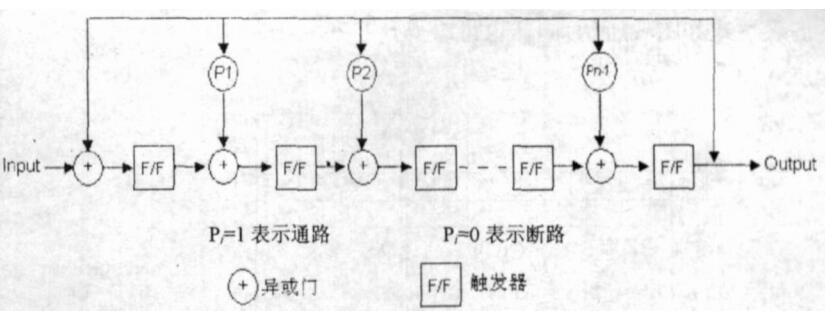
CRC硬件電路的實現很簡單，下圖給出教科書上任意生成多項式G(X)=gnXn+gn-1Xn-1+···+g1X+g0的電路結構：

為什么從右邊輸入data?

因為CRC是除余數，所以從右邊輸入數據，相當于把信息位data先左移位。

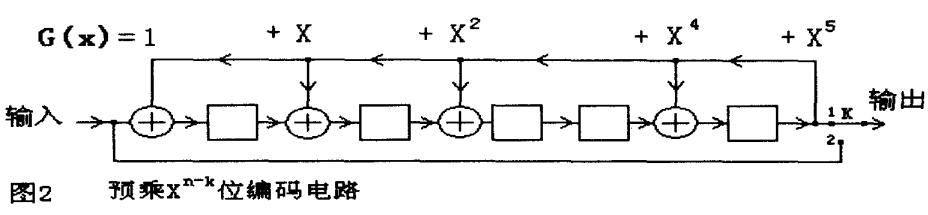
以簡單的CRC8舉例，多項式G(x)=X8 +X7 +X6 +X4 +X2 +1 的電路示意圖如下：

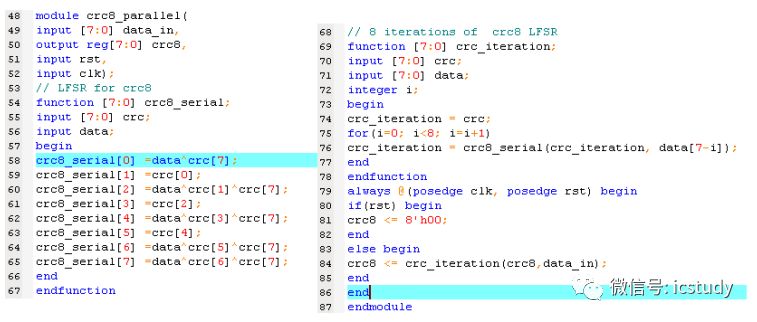
對應的Verilog code代碼如下：

上面的Verilog code上用了LFSR這種變量聲明，有沒有感到奇怪？

LFSR（線性移位寄存器）和CRC的算法很像的，有興趣的可去看看LFSR的相關知識。

一位串行輸入的CRC電路實現方法很簡單，每周期的組合邏輯鏈路簡單延時短。它的缺點是輸入位寬只有一位，所以一個clock周期只能算一位，如果是64bit的信息位就要64個clock周期。如果需要傳輸的位數比較多，會對系統的性能產生比較大的影響。

假設要把輸入位寬變成8位（byte）輸入，電路將是什么樣的呢？并行的CRC其實也簡單，可以用提前抽取的概念來實現。

用下圖來解釋一下，CRCM有M個校驗位就是有M個寄存器，現在把輸入變成N位。

提前抽取就是通過關系函數得到下一個clock寄存器的輸入nxt_crc[M-1:0]：

關系函數CN如下：

nxt_crc=CN(crc_out,data)，

crc_out是前一個clock的寄存器輸出；

data是當前的輸入數據；

函數CN就是一個組合邏輯網絡，也可叫做所謂的scramble。怎樣得出這個CN呢？如果數字信號處理學的好，可以去推導一下。網上有各種算法，很多很多。下面介紹一種方法。

2

以CRC8，G(x)=X8 +X7 +X6 +X4 +X2 +1為例子產生一個CRC8_8的CN，下面直接給出CRC8_8的Verilog code，后面講怎么得到這個CN。

上面的Verilog code 的代碼是由下面的矩陣得出的

把N_in作為數據，M_in作為CRC的上一個clock的值就有：

LFSR_S[0] =DATA[0]^DATA[1]^DATA[3]^DATA[6]^DATA[7]^LFSR_N[0]^LFSR_N[1]^LFSR_N[3]^LFSR_N[6]^LFSR_N[7];

怎么獲得這個矩陣呢?

CRCM_N(M_in,N_in)= CRCM_N(M_in,0)+ CRCM_N(0,N_in)

可以用crc8_parallel(N_in)：輸入data_in 的是8‘b00000001，得到crc8的值，就是H1的第一行8’hd5；輸入data_in 的是8‘b00000010，得到crc8的值，就是H1的第二行8’h7f；以此類推。計算出上面矩陣H1=[]NxM。計算H2=[]MxM的方法和H1是一樣的。

有上面的矩陣就有CN函數。有了CN就可很容易得出CRC硬件電路了。上面的方法其實可寫成一個腳本，實現任意多項式任意位寬輸入的并行CRC硬件電路。www.OutputLogic.com 有自動生成器，不過大家最好自己寫一寫。提醒：上面有LSB和MSB誰先輸入到并行CRC里面去的問題？琢磨一下吧！