隱馬爾可夫模型(Hidden Markov Model,HMM)是統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數,然后利用這些參數來作進一步的數據分析,例如模式識別。
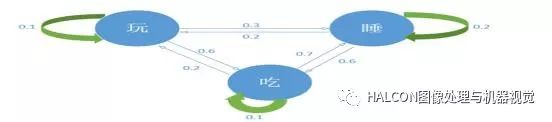
HMM在建模的系統被認為是一個馬爾可夫過程與未觀測(隱藏的)到狀態的統計馬爾可夫模型。一般來說,HMM中說到的馬爾可夫鏈其實是指隱含狀態鏈,因為隱含狀態之間存在轉換概率。
可見狀態之間沒有轉換概率,但是隱含狀態和可見狀態之間有一個做輸出概率。如果提前知道所有隱含狀態之間的轉換概率和所有隱含狀態到所有可見狀態之間的輸出概率,做模擬是相當容易的。

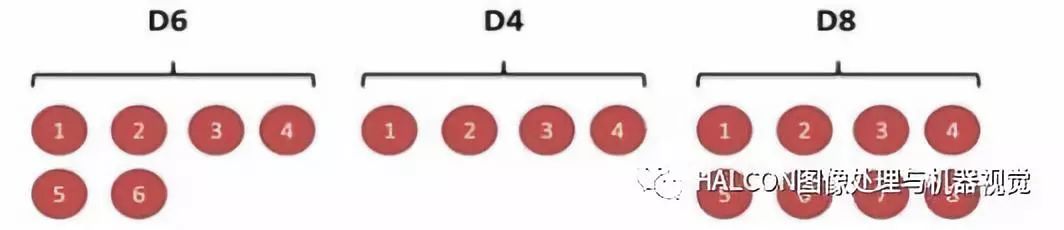
通過下圖骰子例子說明:第一個骰子是我們平常見的骰子(稱骰子為D6),6個面,每個面(1,2,3,4,5,6)出現的概率是1/6。第二個骰子是個四面體(稱骰子為D4),每個面(1,2,3,4)出現的概率是1/4。第三個骰子有八個面(稱骰子為D8),每個面(1,2,3,4,5,6,7,8)出現的概率是1/8。
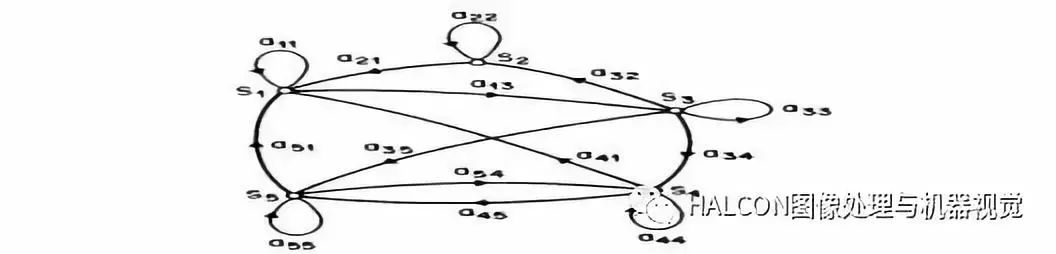
HMM模型相關的算法主要分為三類:
1、知道骰子有幾種(隱含狀態數量),每種骰子是什么(轉換概率),根據擲骰子擲出的結果(可見狀態鏈),我想知道每次擲出來的都是哪種骰子(隱含狀態鏈)。這個問題有兩種解法,給出兩個不同的答案。

第一種解法求最大似然狀態路徑,說通俗點呢,就是求一串骰子序列,這串骰子序列產生觀測結果的概率最大。第二種解法,就不是求一組骰子序列了,而是求每次擲出的骰子分別是某種骰子的概率。
2、知道骰子有幾種(隱含狀態數量),每種骰子是什么(轉換概率),根據擲骰子擲出的結果(可見狀態鏈),我想知道擲出這個結果的概率。看似這個問題意義不大,因為擲出來的結果很多時候都對應了一個比較大的概率。

問這個問題的目的呢,其實是檢測觀察到的結果和已知的模型是否吻合。如果很多次結果都對應了比較小的概率,那么就說明我們已知的模型很有可能是錯的,有人偷偷把我們的骰子給換了。
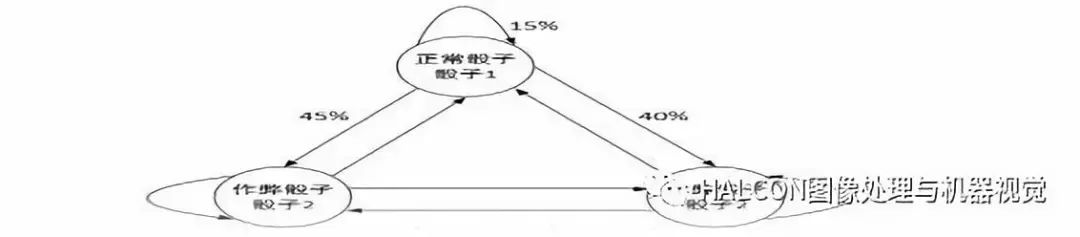
3、知道骰子有幾種(隱含狀態數量),不知道每種骰子是什么(轉換概率),觀測到很多次擲骰子的結果(可見狀態鏈),我想反推出每種骰子是什么(轉換概率)。

這是最常見的情況,很多時候我們只有可見結果,不知道HMM模型里的參數,我們需要從可見結果估計出這些參數,這是建模的一個必要步驟。

比如說懷疑自己的六面骰被賭場動過手腳了,有可能被換成另一種六面骰,這種六面骰擲出來是1的概率更大,是1/2,擲出來是2,3,4,5,6的概率是1/10。怎么辦么?答案很簡單,算一算正常的三個骰子擲出一段序列的概率,再算一算不正常的六面骰和另外兩個正常骰子擲出這段序列的概率。如果前者比后者小,就要小心了。比如說擲骰子的結果是:

要算用正常的三個骰子擲出這個結果的概率,其實就是將所有可能情況的概率進行加和計算。同樣,簡單而暴力的方法就是把窮舉所有的骰子序列,還是計算每個骰子序列對應的概率,把所有算出來的概率相加,得到的總概率就是我們要求的結果。解決這個問題的算法叫做前向算法,如果我們只擲一次骰子:

看到結果為1,產生這個結果的總概率可以按照如下計算,總概率為0.18:

把這個情況拓展,我們擲兩次骰子:

看到結果為1,6.產生這個結果的總概率可以按照如下計算,總概率為0.05:

繼續拓展,我們擲三次骰子:

看到結果為1,6,3,產生這個結果的總概率可以按照如下計算,總概率為0.03:

同樣的,我們一步一步的算,有多長算多長,再長的馬爾可夫鏈總能算出來的。用同樣的方法,也可以算出不正常的六面骰和另外兩個正常骰子擲出這段序列的概率,然后我們比較一下這兩個概率大小,就能知道你的骰子是不是被人換了。

-
建模
+關注
關注
1文章
315瀏覽量
61199 -
數據分析
+關注
關注
2文章
1467瀏覽量
34503 -
隱馬爾可夫
+關注
關注
0文章
7瀏覽量
6569
原文標題:隱馬爾可夫模型
文章出處:【微信號:NeXt8060,微信公眾號:HALCON圖像處理與機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于隱馬爾可夫模型的音頻自動分類
基于隱馬爾可夫預測的功率博弈機制





















評論