對于大多數數據科學家而言，線性回歸方法是他們進行統計學建模和預測分析任務的起點。但我們不可夸大線性模型（快速且準確地）擬合大型數據集的重要性。如本文所示，在線性回歸模型中，「線性」一詞指的是回歸系數，而不是特征的 degree。

特征（或稱獨立變量）可以是任何的 degree，甚至是超越函數（transcendental function），比如指數函數、對數函數、正弦函數。因此，很多自然現象可以通過這些變換和線性模型來近似模擬，即使當輸出與特征的函數關系是高度非線性的也沒問題。

另一方面，由于 Python 正在快速發展為數據科學家的首選編程語言，所以能夠意識到存在很多方法用線性模型擬合大型數據集，就顯得尤為重要。同樣重要的一點是，數據科學家需要從模型得到的結果中來評估與每個特征相關的重要性。

然而，在 Python 中是否只有一種方法來執行線性回歸分析呢？如果有多種方法，那我們應該如何選擇最有效的那個呢？

由于在機器學習中，Scikit-learn 是一個十分流行的 Python 庫，因此，人們經常會從這個庫調用線性模型來擬合數據。除此之外，我們還可以使用該庫的 pipeline 與 FeatureUnion 功能（如：數據歸一化、模型回歸系數正則化、將線性模型傳遞給下游模型），但是一般來看，如果一個數據分析師僅需要一個又快又簡單的方法來確定回歸系數（或是一些相關的統計學基本結果），那么這并不是最快或最簡潔的方法。

雖然還存在其他更快更簡潔的方法，但是它們都不能提供同樣的信息量與模型靈活性。

請繼續閱讀。

有關各種線性回歸方法的代碼可以參閱筆者的 GitHub。其中大部分都基于 SciPy 包

SciPy 基于 Numpy 建立，集合了數學算法與方便易用的函數。通過為用戶提供高級命令，以及用于操作和可視化數據的類，SciPy 顯著增強了 Python 的交互式會話。

以下對各種方法進行簡要討論。

方法 1：Scipy.polyfit( ) 或 numpy.polyfit( )

這是一個非常一般的最小二乘多項式擬合函數，它適用于任何 degree 的數據集與多項式函數（具體由用戶來指定），其返回值是一個（最小化方差）回歸系數的數組。

對于簡單的線性回歸而言，你可以把 degree 設為 1。如果你想擬合一個 degree 更高的模型，你也可以通過從線性特征數據中建立多項式特征來完成。

詳細描述參考：https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.polyfit.html。

方法 2：stats.linregress( )

這是 Scipy 中的統計模塊中的一個高度專門化的線性回歸函數。其靈活性相當受限，因為它只對計算兩組測量值的最小二乘回歸進行優化。因此，你不能用它擬合一般的線性模型，或者是用它來進行多變量回歸分析。但是，由于該函數的目的是為了執行專門的任務，所以當我們遇到簡單的線性回歸分析時，這是最快速的方法之一。除了已擬合的系數和截距項（intercept term）外，它還會返回基本的統計學值如 R2 系數與標準差。

詳細描述參考：http://blog.minitab.com/blog/adventures-in-statistics-2/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-goodness-of-fit

方法 3：optimize.curve_fit( )

這個方法與 Polyfit 方法類似，但是從根本來講更為普遍。通過進行最小二乘極小化，這個來自 scipy.optimize 模塊的強大函數可以通過最小二乘方法將用戶定義的任何函數擬合到數據集上。

對于簡單的線性回歸任務，我們可以寫一個線性函數：mx+c，我們將它稱為估計器。它也適用于多變量回歸。它會返回一個由函數參數組成的數列，這些參數是使最小二乘值最小化的參數，以及相關協方差矩陣的參數。

詳細描述參考：https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html

方法 4：numpy.linalg.lstsq

這是用矩陣因式分解來計算線性方程組的最小二乘解的根本方法。它來自 numpy 包中的線性代數模塊。通過求解一個 x 向量（它將|| b—a x ||2的歐幾里得 2-范數最小化），它可以解方程 ax=b。

該方程可能會欠定、確定或超定（即，a 中線性獨立的行少于、等于或大于其線性獨立的列數）。如果 a 是既是一個方陣也是一個滿秩矩陣，那么向量 x（如果沒有舍入誤差）正是方程的解。

借助這個方法，你既可以進行簡單變量回歸又可以進行多變量回歸。你可以返回計算的系數與殘差。一個小竅門是，在調用這個函數之前，你必須要在 x 數據上附加一列 1，才能計算截距項。結果顯示，這是處理線性回歸問題最快速的方法之一。

詳細描述參考：https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.linalg.lstsq.html#numpy.linalg.lstsq

方法 5： Statsmodels.OLS ( )

statsmodel 是一個很不錯的 Python 包，它為人們提供了各種類與函數，用于進行很多不同統計模型的估計、統計試驗，以及統計數據研究。每個估計器會有一個收集了大量統計數據結果的列表。其中會對結果用已有的統計包進行對比試驗，以保證準確性。

對于線性回歸，人們可以從這個包調用 OLS 或者是 Ordinary least squares 函數來得出估計過程的最終統計數據。

需要記住的一個小竅門是，你必須要手動為數據 x 添加一個常數，以用于計算截距。否則，只會默認輸出回歸系數。下方表格匯總了 OLS 模型全部的結果。它和任何函數統計語言（如 R 和 Julia）一樣豐富。

詳細描述參考：http://www.statsmodels.org/dev/index.html

方法 6、7：使用矩陣求逆方法的解析解

對于一個良態（well-conditioned）線性回歸問題（至少是對于數據點、特征），回歸系數的計算存在一個封閉型的矩陣解（它保證了最小二乘的最小化）。它由下面方程給出：

在這里，我們有兩個選擇：

方法 6：使用簡單矩陣求逆乘法。

方法 7：首先計算數據 x 的廣義 Moore-Penrose 偽逆矩陣，然后將結果與 y 進行點積。由于這里第二個步驟涉及到奇異值分解（SVD），所以它在處理非良態數據集的時候雖然速度慢，但是結果不錯。（參考：開發者必讀：計算機科學中的線性代數）

詳細描述參考：https://en.wikipedia.org/wiki/Linear_least_squares_%28mathematics%29

方法 8： sklearn.linear_model.LinearRegression( )

這個方法經常被大部分機器學習工程師與數據科學家使用。然而，對于真實世界的問題，它的使用范圍可能沒那么廣，我們可以用交叉驗證與正則化算法比如 Lasso 回歸和 Ridge 回歸來代替它。但是要知道，那些高級函數的本質核心還是從屬于這個模型。

詳細描述參考：http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html

以上方法的速度與時間復雜度測量

作為一個數據科學家，他的工作經常要求他又快又精確地完成數據建模。如果使用的方法本來就很慢，那么在面對大型數據集的時候便會出現執行的瓶頸問題。

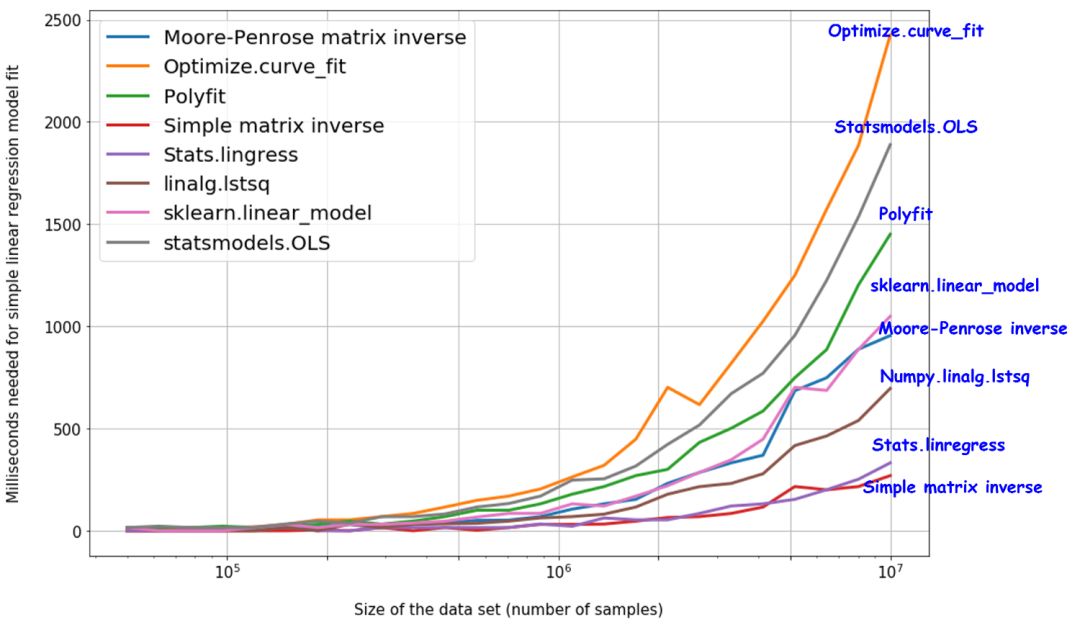
一個判斷算法能力可擴展性的好辦法，是用不斷擴大的數據集來測試數據，然后提取所有試驗的執行時間，畫出趨勢圖。

可以在 GitHub 查看這個方法的代碼。下方給出了最終的結果。由于模型的簡單性，stats.linregress 和簡單矩陣求逆乘法的速度最快，甚至達到了 1 千萬個數據點。

總結

作為一個數據科學家，你必須要經常進行研究，去發現多種處理相同的分析或建模任務的方法，然后針對不同問題對癥下藥。

在本文中，我們討論了 8 種進行簡單線性回歸的方法。其中大部分方法都可以延伸到更一般的多變量和多項式回歸問題上。我們沒有列出這些方法的 R2 系數擬合，因為它們都非常接近 1。

對于（有百萬人工生成的數據點的）單變量回歸，回歸系數的估計結果非常不錯。

這篇文章首要目標是討論上述 8 種方法相關的速度/計算復雜度。我們通過在一個合成的規模逐漸增大的數據集（最大到 1 千萬個樣本）上進行實驗，我們測出了每種方法的計算復雜度。令人驚訝的是，簡單矩陣求逆乘法的解析解竟然比常用的 scikit-learn 線性模型要快得多。