姿態探測指在三維空間中測量物體的方向和旋轉，這種技術對于飛機與航天器的導航至關重要。最近的研究證實，環形激光陀螺儀和纖維環陀螺儀能夠替代傳統的機械陀螺儀，精確地測量旋轉運動。此裝置的基本工作原理是一種被稱作薩格納克效應的光學現象。在本文中，我們將利用射線光學仿真，觀察簡單薩格納克干涉器中的薩格納克效應。

究竟是我還是房間在旋轉？

任何導航系統的一項基本任務是保持追蹤物體的位置和方向，以及二者的變化率。導航系統對精度的要求達到了極致，特別是太空航行領域。舉例來說，通信衛星可以敏感地響應千分之一度每小時的細微角速度。

系統對精度的要求固然令人生畏，不過事實上姿態控制的基本任務可以歸納為一個簡單的問題：如何確定我的旋轉速度以及旋轉軸？

原則上講，對于任意旋轉坐標系中的任何觀測者而言，這個任務都是相同的，即便是旋轉餐廳中的賓客也不例外。

印度國賓大酒店的旋轉餐廳的照片，它是印度歷史最悠久的旋轉餐廳。該照片由 AryaSnow 拍攝，已獲 CC BY-SA 4.0 授權，并通過 Wikimedia Commons 共享。

假設你坐在旋轉餐廳里面就餐，現在正在推斷餐廳的角速度 Ω（單位：rad/s）。

最簡單的方法就是往外看。選取一個靜止的目標，比如建筑物或樹，然后觀察在你的視野中它的位置是否會隨時間變化。

上圖展示了在觀察者的視野中（比如從窗戶往外看），樹在初始時間 t1 和時間 t2 時的位置。設兩個視線之間的角度為 θ（單位：度）。如果相對于餐廳本身的大小，樹的距離很遠，角速度的計算公式則為

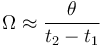
太空中的相似場景

太空航行的難度比在餐廳吃飯大得多，所以我們必須注意幾個額外事項。在太空中，“靜止物體”的方法比較難實現。舉例來說，當我們利用太陽敏感器對地球靜止軌道上的衛星進行姿態控制時，還要考慮地球繞太陽轉動的相對運動。相比之下，恒星敏感器的精度極其可靠，這是因為基于各種目標前提，我們可以認為恒星在太空的位置是始終不變的，且恒星更接近于一個光點，而不是有一定角度的連續光源。

除此之外，在航天器姿態測量與控制對精度的嚴苛標準下，被觀測物體的有限尺寸也需要考慮到，比如當你看向太陽時，要知道自己在觀察太陽的哪一部分。在三維空間中實現任意旋轉至少需要兩個物體，否則你不能判斷旋轉軸的方向。

遮住視野

現在我們又回到原來的餐廳，只不過這次窗戶都關上了。既然向外看的視線被遮擋住了，你不能依賴于任何物體來判斷旋轉坐標系。

我們可以在旋轉坐標系內做幾個實驗來確定它的角速度。比如在地板上放一個球，觀察離心力是否會使它滾動（這時你需要知道旋轉軸的位置——在太空航行中可不一定行?。?。另一個方法是使用機械陀螺儀。

下個章節將解釋第三種方法——利用光的特性；準確地說，真空中的光在所有坐標系中擁有相同速度的特性。光在旋轉坐標系中傳播時，它揭示了一種被稱作薩格納克效應的現象。環形激光陀螺儀 就是利用了這種效應。這種陀螺儀廣泛取代了利用高速回轉體的傳統機械式陀螺儀，環形激光陀螺儀舍棄了活動部件，因此維護成本更低。

解釋薩格納克效應

觀察薩格納克效應最簡單的方法是：利用兩束在同一個圓環中對向傳播——即反向運動——的光線。圓環以恒定的角速度 Ω 逆時針旋轉。（國際單位是弧度每秒，不過在慣性導航系統中，我們可以用度每秒來代替它。）

初始時，兩束光線從圓環的 P0 點發射，沿圓環以光速反向傳播，與此同時，發射點開始繞坐標系旋轉。當沿順時針方向傳播的光線與發射點再次重合時，重合點為一個新的位置 P1，傳播距離略小于一個完整的圓。當沿逆時針方向傳播的光線與發射點重合時，重合點為另一個不同的位置 P2，其傳播距離大于一個完整的圓。

當然，這里的運動顯然被夸大了。在現實中，P0 同 P1 和 P2（以及后者之間）的位移可能小一百億倍！但是因為兩束光線的距離差伴隨著相移，而相移會在兩束光線之間產生干涉圖案，所以兩束光線的傳播距離的細微差別（同理還有傳播時間）還是可檢測到的。若設 ΔL 為兩束光線傳播的距離差，則

(1)

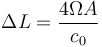
其中，A 是圓環面積，真空光速為 c0 = 299,792,458 m/s。

事實證明，方程 (1) 不僅符合環形路徑，也適用于其他形狀。光程差只取決于環路的封閉面積，而不是形狀。我們可以根據廣義相對論推導出方程 (1) 的一般表達式。方程的核心在于，薩格納克效應是一種相對論現象，對于這種現象，經典推導可以得到相同的一階結果。參考文獻 1–2。

利用射線光學仿真演示薩格納克效應

在本節中，我們將研究簡單的薩格納克干涉儀模型。它的基本工作原理與環形激光陀螺儀相同，不過前者不需要考慮光束路徑上的激光介質，所以模型創建步驟更加簡單。（除了強度更大之外，激光介質還會引入很多其他復雜性，比如色散效應，不過為了方便描述，我們可以忽略。）但是，對于給定的薩格納克干涉儀模型幾何與擁有相同鏡子布局的環形激光干涉儀，二者會產生同樣的光程差和相位延遲，所以這個模型依舊可以提供大量信息。

基本的薩格納克干涉儀幾何由一個分光器、兩面鏡子和一個可吸收射出光線的障礙物組成。圖示如下。

此模型的幾何參數見下表。

參數名稱	公式	值	描述
λ0	N/A	632.8 nm	真空波長
R	N/A	10 cm	圓環半徑
b		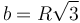17.3 cm	三角形邊長
P		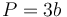52.0 cm	三角形周長
A		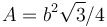130 cm2	三角形面積

幾何結構有時被設計成正方形，而不是三角形，這時三個鏡子位于三個頂點上，分光器在另一個頂點上。系統中光線的傳播路徑通過方向箭頭來表示。由于整個裝置沿逆時針方向旋轉，因此在碰到障礙物之前，沿逆時針方向發射的光線比順時針光線的傳播距離稍遠一些。

為了直觀演示這一現象，請觀看下方動畫（請注意，旋轉運動又被夸大了一百億倍！）。

在第一個動畫中，觀察者站在慣性（非加速）坐標系中。雖然光線的傳播路徑都是直線，但是它們撞擊鏡子的時間卻不一樣。在第二個動畫中，觀察者“乘坐”著宇宙飛船，可視為身處非慣性坐標系中（嚴格來說，即使在旋轉坐標系中，對向傳播的光線的運動速度也相同；任何坐標系中光速均不變?。?。

代入上文給出的幾何結構參數，方程 (1) 計算出兩束對向傳播光線之間的光程差為 8 × 10-16 米，即 0.8 飛米，約等于質子的半徑；這個數值顯然很難測量！薩格納克干涉儀和環形激光陀螺儀通常不會直接給出光程長，而是報告頻率差或者拍頻 Δν，其公式為：

(2)

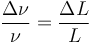
其中 ν（Hz）是光的頻率，L 是沿三角形周長傳播的光的光程長度。

注意，L 不一定是三角形的周長，因為系統中可能存在共用運動的介質，比如沿光束路徑、折射率不等于 1（n ≠ 1）的激光介質。在本例中，假設鏡子和分光器之間為真空空間。則拍頻的數量級為 1 Hz，當然比質子半徑的距離容易測量得多。

該模型利用幾何光學 接口來追蹤薩格納克干涉儀幾何中的光線。兩個鏡子被施加了專門產生鏡面反射的鏡像 邊界條件。分光器采用了材料不連續性 邊界條件，用戶定義的反射比為 0.5，所以兩個對向傳播光束具有相同的強度。

我們還利用了旋轉域 特征使裝置旋轉，如下圖所示：

所得繪圖顯示了鏡面光學系統中沿兩個方向傳播的光線，然而由于與光速相比，鏡子的移動速度非常慢，所以我們很難將兩個路徑區分開。如果放大一百億左右，才能辨別出兩個隔著微小距離的三角形。

在下方繪圖中，拍頻是干涉儀角速度的函數。二者函數關系是線性的，符合方程 (1)–(2)。繪圖左下角出現了一些數值噪聲。這是數值精度造成的，在模型文檔中將解釋更多細節。

姿態探測應用于航空航天導航

上文提到的薩格納克干涉儀和相關裝置——包括環形激光陀螺儀和光纖陀螺儀——都屬于慣性導航系統的現實應用；慣性導航系統以一個已知位置為起點，將平移速度和角速度隨時間的變化整合在一起，從而預測物體的位置和方向?，F實中，慣性導航系統通常需要與以太空中其他物體為參照物的絕對位置和絕對方向測量相結合。絕對測量可以利用地球敏感器、太陽敏感器或恒星敏感器；利用地球表面已知位置上的射頻信標；利用地球磁場測量；或者利用以上任意組合來完成。

平移速度和角速度的微小測量誤差會導致慣性導航系統隨時間推移變得越來越不穩定。使用以上任意一種敏感器定期進行絕對測量，有利于將不確定性限制在一個更合理的數值內。下圖預測了不確定性隨時間的變化。

結論

我們成功地利用射線光學仿真演示了簡單干涉儀內的薩格納克效應。只要所有活動部件的速度遠遠小于光速，拍頻便符合基于廣義相對論的嚴密理論。薩格納克干涉儀或環形激光陀螺儀之內的光程差的大小僅僅取決于對向傳播光束所圍住的面積，而非圓環的幾何結構。