1、引言
目標識別作為現代雷達的重要發展方向之一,成為未來武器系統中的一個重要組成部分和當前國內外關注的熱點,具有廣泛的民用和軍事應用價值。根據雷達的探測手段及應用背景的不同,出現了多種識別方法,其中雷達成像識別技術作為雷達目標識別的一種新技術正在日趨成熟。而與二維成像雷達相比,易于實現的一維成像雷達(高距離分辨率雷達)在目標識別方面有著廣闊的前景。
文獻[1]對基于一維距離像的子空間方法進行了廣泛而深入的研究,在普通特征子空間的基礎上,提出了正則子空間法、修正特征子空間法、綜合子空間法、子空間串法等多種子空間法,在對仿真與實測數據的識別中均取得較好的效果。其中部分算法的FPGA實現研究正是本文研究的主要任務。
CORDIC算法(The Coordinate Rotation Digital Com-puter)是Voider等人于1959年在美國航空控制系統的設計中提出來的,他是一種用于計算一些常用的基本運算函數和算術操作的循環迭代算法,其基本思想是用一系列與運算基數相關的角度的不斷偏擺從而逼近所需旋轉的角度。本質上講他是一個數值性計算逼近的方法,由于這些固定的角度與計算基數有關,運算只有移位和加減。可用該算法來計算的函數包括乘、除、平方根、正弦、余弦、反正切、向量旋轉(既復數乘法)以及指數運算等。1971年,J.S.Walther提出了統一的CORDIC算法形式,把圓周旋轉、雙曲旋轉和直線旋轉統一到同一個CORDIC迭代方程里。為同一硬件實現多功能提供了前提,隨著VLSI技術的發展,CORDIC算法越來越受到研究與應用人員的重視,Xilinx公司于2002年發布了其CORDIC的IP核,由于IP核技術的可重用特性,可以使CORDIC算法獲得更廣泛的應用。
2、CORDIC原理
CORDIC算法的原始思想一經提出,就受到了人們的普遍關注,隨著FPGA技術的發展,CORDIC獲得了愈來愈廣泛的應用,CORDIC算法可以分解為一些簡單的且在硬件中容易實現的基本算法,如加法、移位等,使得這些算法在硬件上可以得到較好的實現。又因為該算法是一種規則化的算法,他滿足了硬件對算法的模塊化、規則化的要求,因此CORDIC算法可以充分發揮硬件的優勢,利用硬件的資源從而實現硬件與資源相結合的一種優化方案,下面簡要介紹其基本原理。
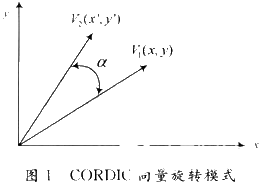
若將向量[z,y]T沿逆時針方向旋轉角度a如圖1所示,初始向量V1經旋轉a角以后得到向量V2。
![]()
也即:
![]()
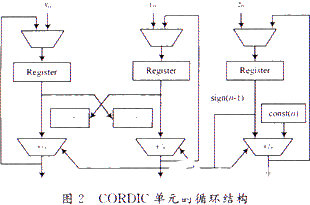
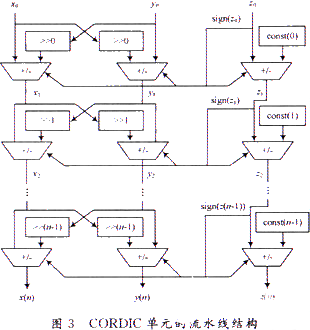
在應用過程中,CORDIC的實現方式我們主要討論循環結構(圖2)以及流水線結構(圖3)。圖2采用的是并行的數據格式,由于其大的扇人量,不適合在單個邏輯單元扇入量有限的FPGA上實現。如果在FPGA上實現將會占用大量的邏輯塊,浪費資源,而且路徑的拉長會導致其速度的降低。在圖3所示的流水線結構中,每一個移位器都是固定的深度,而且旋轉角度集的各個值作為常數值直接連到角累加器件上面,不需要存取空間和讀取時間。在FPGA器件中每個細胞元都有寄存器,便于采用流水線技術。
3、實現技術中的IP核的應用
在實際的設計中,我們采用了Xilinx系列芯片中的IP核來完成設計,這樣做的目的主要是為了充分利用芯片的內部資源,實現內部結構的優化設計,IP核生成工具可以是各種類型、功能的模塊。這些IP核是根據Xilinx的FP-GA器件特點和結構而設計,直接用Xilinx FPGA底層硬件原語進行描述,可充分將FPGA的性能發揮出來,其實現結果在面積和速度上都能達到令人滿意的效果。
4、數值精度問題
在應用每一個數值實現方法時,他的數值精度是我們不得不考慮的問題,CORDIC算法也不例外。WaltherHu、Kota都對他進行了深入的研究,分別對其定點和浮點實現方式的數值精度給出了定量描述或在數學上進行了分析,不同的算法模式不同的操作模式有著不同的結果。CORDIC的誤差主要來自兩方面:一方面,在用旋轉角度集來表示角度時,有限子集產生了截斷誤差;另一方面由于有限字長的限制,在數據表示和移位運算中產生了舍人誤差。由于CORDIC的3個方程之間相互作用,這為分析CORDIC的誤差帶來了很大的難度。以旋轉模式的誤差分析為例,我們以x,y,z表示有限精度下的計算值,xi,yi,zi表示無誤差的精確值,z,y,z表示數學意義上得到的值,旋轉模式時的迭代方程為:
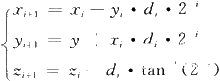
其中:
![]()
經n次迭代后得到:
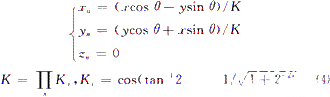
對于x,y分量來說,若假定z分量對他們的作用因子di是精確的,則他們主要是受舍入誤差的影響,設x,y由t1位表示,且均為小數位,則有限精度下的x,y分量經過n次迭代后將產生大約log2n位的舍入誤差。對于z分量來說,其誤差主要來自兩方面:一方面是截斷誤差,設為ezl,由CORDIC收斂性可知:
![]()
另一方面是舍人誤差ez2,若假定用t2來表示z分量則│ez2│《2-t2,假定θ為精確值,a為計算值,則:
![]()
綜上有:
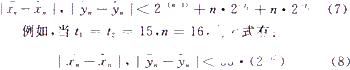
從上面結果中,我們發現只要在算法內部數據中增加log332Δ5位長度的保護位,則可以校正誤差,在輸出結果中獲得15位的精度。
5、 仿真實驗
在實現了各種處理單元以后,我們可以很方便地將其應用于陣列中來計算矩陣的奇異值分解。一個2×2矩陣的SVD實際上就是一個旋轉角計算單元與雙邊旋轉計算單元的組合,結構框圖如圖4所示。
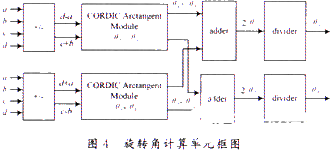
旋轉角計算主要按照直接2-角方法,分別計算出θr+θt和θr-θt,通過加法器和減法器以及除法器,得到θr和θt。一個2×2矩陣的雙邊旋轉為:
![]()
在設計中,我們注意到角θr要等到θt,旋轉完成后才輸入到旋轉器中,我們通過添加FIFO做為延時控制單元,通過控制FIFO的深度來完成數據的同步,獲得同時鐘頻率一樣高的數據流量。雙邊旋轉實現框圖如圖5所示。
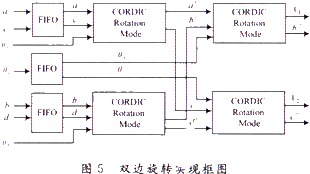
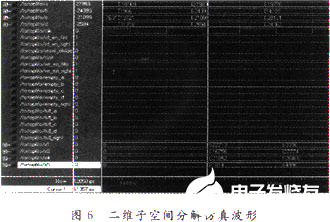
使用VHDL語言進行模塊功能描述,在Xilinx仿真平臺ISE 7.1以及Modelsim SE 5.7d環境下的仿真結果如圖6所示,系統工作的時鐘頻率為50 MHz,在選用高端的Virtcx4系列芯片進行算法的時序仿真時,資源的占用都是比較少的。這為下一步的高階子空間算法的實現奠定了比較好的基礎。
6 、結 語
本文在基于Xilinx的軟硬件開發平臺上,對用FPGA實現用于雷達一維像目標識別的特征子空間方法進行了一系列的探討與研究,深入研究了CORDIC理論在數值精度、操作模式上的各種應用,并且用于FPGA設計實現二維子空間的研究并且成功地進行了硬件仿真實現,下面的工作是結合并行雅可比方法采用Systolic陣列結構進行高階子空間分解的FPGA實現,這部分工作將在后面的研究中完成。
責任編輯:gt
-
FPGA
+關注
關注
1640文章
21903瀏覽量
611475 -
Xilinx
+關注
關注
73文章
2178瀏覽量
123828 -
雷達
+關注
關注
50文章
3034瀏覽量
118995
發布評論請先 登錄
相關推薦
基于DSP和FPGA組合的嵌入式圖像處理平臺的實時多目標識別算法
開發者手機 AI - 目標識別 demo
RCS目標識別
【PYNQ-Z2申請】圖像目標識別FPGA硬件加速
感知起源招聘FPGA工程師(坐標北京)
一種適用于空間觀測任務的實時多目標識別算法分享
基于DSP的毫米波主被動復合探測器目標識別系統設計【回映分享】
基于USB和目標識別的圖像采集系統的設計實現
紅外目標識別跟蹤系統的DSP+FPGA實現



















評論