1 引言

生命信號由于受到人體等諸多因素的影響，具有信號弱、噪聲強、頻率范圍較低和隨機性強的特點，用傳統的傅里葉變換提取具有局限性。而具有多分辨分析特性的小波變換，可利用時頻平面上不同位置的不同分辨率，有效地從非平穩信號中提取瞬態信息，可有效地提取信號的波形。

2 Mallat算法

小波的多分辨分析理論研究表明，滿足一定正則條件的濾波器組可以迭代計算出小波，Mallat 提出了雙尺度方程以及塔式分解算法，這些成果將濾波器組和小波緊密聯系在一起，使得濾波器組與小波理論及設計有了非常緊密的聯系。眾學者開始重視利用濾波器組設計小波，以及濾波器組自身理論的研究。

小波變換的多分辨分析MRA（Multi-Resolution-Analysis）特性，定義空間L2（R）中的一列子空間{Vj}j∈z,稱為L2（R）的一個多分辨分析（MRA），該序列若滿足下列條件：

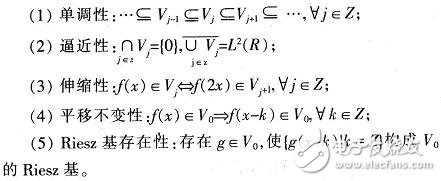
Mallat根據多分辨分析提出小波變換分解和重構快速算法-Mallat算法。設（{Vm;m∈Z}；φ（t））是一個正交MRA，則存在{hk}∈ι2，使雙尺度方程：

方程(1)成立，并利用式(1)可得到尺度函數φ(x)構造函數：

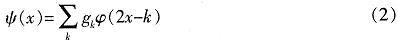
ψ(x)的伸縮、平移構成L2(R)正交基，其中gk=(-1)h1-k。進一步，當

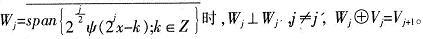
主要包含3個方面的內容：

(1)集合ψ0={φ(x-k)；k∈Z}構成W0的標準正交基，因此構成Wj的標準正交基；

(2)可以保證從而保證Wj的基向量，并可表示L2(R)中的任意函數。

(3)Wj⊥Wj'，j≠j'，保證在彼此正交的前提下當且僅當表示信息。

多分辨分析理論為信號局部分析提供相當直觀的框架，這一點在非平穩信號中的作用尤為重要，代表信號的主要輪廓；而快變部分對應于信號的高頻信息，表示信號的細節，因此，Mallat算法的基本思想可以歸納如下：

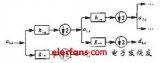
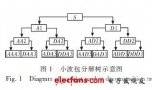
設Hjf為能量有限的信號f∈L2（R）在分辨率2j下的近似，則Hjf可以進一步分解為f在分辨率2j-1下的近似Hj-1f,以及位于分辨率2j-1與2j之間的細節Dj-1f之和，其分解和重構過程如圖1和圖2所示。

3 小波閾值去噪法

一般含噪的一維信號的模型可表示為：

s（k）=f（k）+εe（k），k=0，1，…n-1 （3）

式中，s（k）為含噪信號，f（k）為有用信號，e（k}）為噪聲信號。

利用小波檢測微弱生命信號的實質是提取強噪聲背景下的生命信號，這個過程即去噪，在小波去噪的方法中比較常用的是閾值去噪法。

小波閾值去噪可分為3部分：

（1）信號的小波分解選擇一個小波函數對信號進行分解計算。

（2）小波分解高頻系數的閡值量化 對各分解尺度下的高頻系數選擇一個閾值進行閾值量化處理。

（3）小波重構 根據小波分解的最底層低頻系數和各層高頻系數進行小波重構。

最關鍵的是閾值的選擇以及閾值的量化，該步驟完成的好壞決定信號消噪的質量。在閾值去噪中，閾值函數體現了對超過和低于閾值的小波系數模的不同處理策略以及不同估計方法。設ω是原始小波系數，η（ω）表示閾值化后的小波系數，T是閾值，I（x）為示性函數。

常見閾值函數有：（a）硬閾值函數（圖3a），η（ω=ωI（|ω|>T）；（b）軟閾值函數（圖3b），η（ω）=（ω-sgn（ω）T）I（|ω|>T）。

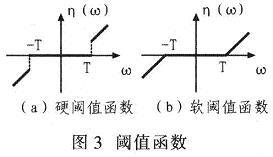
小波閾值去噪方法除閾值函數的選取外，另一個關鍵因素是閾值估計。如果閾值太小，去噪后的信號仍然有噪聲存在；閾值太大，重要的信號特征又被過濾掉，引起偏差。常見的閾值估計方法有Visushrik閾值、SUREShrink閾值、GCV閾值等。設原始信號小波系數估計通過軟閾值函數萎縮得到，即

閾值的選擇可通過下面的風險函數定義：

由于小波變換的正交性，風險函數可以寫成：

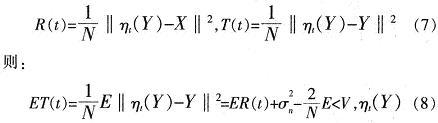
可以證明，當V服從Guass分布時，有下面的等式成立

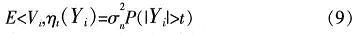
式中，P(|Yi|>t)服從二項分布，其概率可用|Yi|>t出現的頻率近似，可得到風險函數的表達式如下：

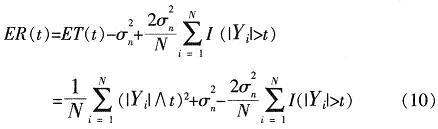
式中，I是示性函數，^表示兩數取小。

則最佳閩值選擇可以通過最小化風險函數得到，即

，對于最佳閾值的選擇可以在一個有限的范同內，即t*∈{Y1，Y2，…，YN}。在實際應用中，SUREShrink閾值去噪法能獲得較為滿意的去噪效果，這是一種誤差較低的閾值去噪方法。

4 小波去噪的MATLAB仿真

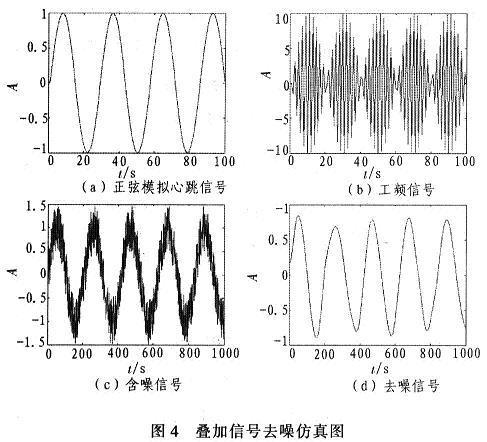
一般檢測到的微弱生命信號的背景強噪聲主要是工頻干擾信號，因此采用正弦信號模擬人體心跳信號頻率為0.7 Hz、幅度是1，模擬的工頻干擾信號頻率為50 Hz、幅度是心跳信號的10倍，和Matlab提供的噪聲noissin信號疊加，可近似組成強噪聲背景下的生命信號，采用db3小波進行信號分解，并對信號進行SUREShrink閾值估計，并采用heursure函數實現。

MATLAB的基本數據單位是矩陣，它的指令表達式與數學、工程中常用的形式十分相似，故用MATLAB來解算問題要比用C，FORTRAN等語言完成相同的事情簡捷得多，并且MATLAB也吸收了像Maple等軟件的優點，使MATLAB成為一個強大的數學軟件。

將信號映射到小波域，根據噪聲和噪聲的小波系數在不同尺度上具有不同的性質和機理，對含噪信號的小波系數進行處理。實質是減少剔除噪聲產生的小波系數，最大限度的保留真實信號的系數。

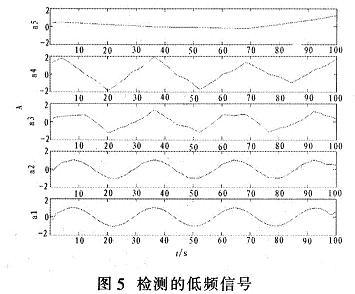
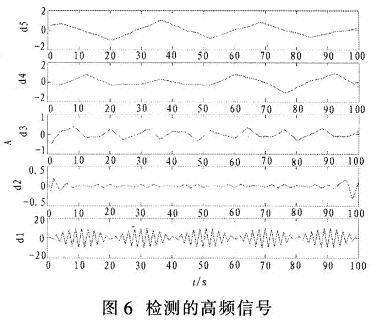
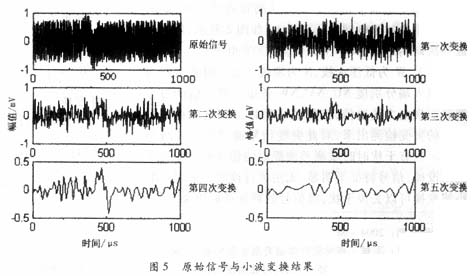
疊加信號去噪仿真圖如圖4所示，疊加信號經過小波閾值去噪法去噪后，可得到較好的生命信號，小波分解和重構的細節，如圖5和圖6所示。根據Mallat算法的基本思想，高頻信號和低頻信號分別可以從圖中反映出來，其中a1和d1分別反映模擬生命信號的正弦信號，和強噪聲干擾的工頻信號，這就說明對微弱生命信號的提取小波可以取得很好的效果，由于這里所使用的是模擬的生命信號，在實際應用時還應進行改進。

5 結束語

生命信號由于本身的特點，傳統的傅里葉變換對其消噪和提取顯得無能為力，因為傅里葉變換對信號的分析只是在頻域中進行，不能反映信號某一點的變化情況，而小波變換可以對信號在時頻兩域進行分析，很適合探測信號的瞬時狀態，對微弱生命信號可以進行有效去噪和提取。通過仿真表明，小波變換很適合微弱生命信號的檢測，可以在這一領域發揮重要作用。