建立有效的用戶瀏覽預測模型,對用戶的瀏覽做出準確的預測,是導航工具實現對用戶瀏覽提供有效幫助的關鍵。
在瀏覽預測模型方面,很多學者都進行了卓有成效的研究。AZER提出了基于概率模型的預取方法,根據網頁被連續訪問的概率來預測用戶的訪問請求。SARUKKAI運用馬爾可夫鏈進行訪問路徑分析和鏈接預測,在此模型中,將用戶訪問的網頁集作為狀態集,根據用戶訪問記錄,計算出網頁間的轉移概率,作為預測依據。SCHECHTER構造用戶訪問路徑樹,采用最長匹配方法,尋找與當前用戶訪問路徑匹配的歷史路徑,預測用戶的訪問請求。XU Cheng Zhong等引入神經網絡實現基于語義的網頁預取。徐寶文等利用客戶端瀏覽器緩沖區數據,挖掘其中蘊含的興趣關聯規則,預測用戶可能選擇的鏈接。朱培棟等人按語義對用戶會話進行分類,根據會話所屬類別的共同特征,預測用戶可能訪問的文檔。
在眾多的瀏覽模型中,Markov模型是一種簡單而有效的模型。Markov模型最早是ZUKERMAN等人于1999年提出的一種用途十分廣泛的統計模型,它將用戶的瀏覽過程抽象為一個特殊的隨機過程——齊次離散Markov模型,用轉移概率矩陣描述用戶的瀏覽特征,并基于此對用戶的瀏覽進行預測。之后,BOERGES等采用了多階轉移矩陣,進一步提高了模型的預測準確率。在此基礎上,SARUKKAI建立了一個實驗系統[9],實驗表明,Markov預測模型很適合作為一個預測模型來預測用戶在Web站點上的訪問模式。
1 Markov模型
1.1 Markov模型
Markov預測模型對用戶在Web上的瀏覽過程作了如下的假設。
假設1(用戶瀏覽過程假設):假設所有用戶在Web上的瀏覽過程是一個特殊的隨機過程——齊次的離散Markov模型。即設離散隨機變量的值域為Web空間中的所有網頁構成的集合,則一個用戶在Web中的瀏覽過程就構成一個隨機變量的取值序列,并且該序列滿足Markov性。
一個離散的Markov預測模型可以被描述成三元組,S代表狀態空間;A是轉換矩陣,表示從一個狀態轉換到另一個狀態的概率;B是S中狀態的初始概率分布。其中S是一個離散隨機變量,值域為{x1,x2,…xn},其中每個xi對應一個網頁,稱為模型的一個狀態。
Markov預測模型是一個典型的無后效性隨機過程,也就是說模型在時刻t的狀態只與它的前一個時刻t-1的狀態條件相關,與以前的狀態獨立。即:

王實等提出一種新的基于隱馬爾可夫模型的興趣遷移模式發現方法,并利用用戶遷移模式間的關聯規則來發現興趣遷移模式。而借助隱馬爾可夫模型, 挖掘蘊涵在用戶訪問路徑中的信息需求概念, 以此進行預取頁面的評價, 也可以實現基于語義的網頁預取。
隱Markov模型盡管考慮了用戶興趣,但和簡單的Markov模型一樣,存在一定的不足:用戶訪問序列串長是動態時變的,采用固定階數的傳統Markov鏈模型并不能準確地對用戶的訪問行為建模。
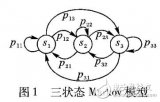
2.2 多Markov模型
雖然用戶在Web空間的瀏覽過程是一個受瀏覽目的、文化背景、興趣愛好等多種因素影響的復雜過程,有很多差異,然而觀察大量用戶的瀏覽過程可以發現,某些用戶的瀏覽過程表現出相同或相近的特點,如他們瀏覽的網頁基本相同,瀏覽各個網頁的順序相似等,這一現象引發了對Web用戶分類的研究。通過對用戶分類,同一類別的用戶用同一個模型來描述它,而不同類別的用戶其瀏覽過程差別較大,用不同的模型來描述他們的特征則更為合理。
假設2(用戶分類假設):假設根據用戶在Web空間的瀏覽特點,可以將所有用戶分為K類。如果用C={c1, c2,…,ck}表示用戶的類別,則任意一個用戶屬于類別ck的概率為P(C=ck),而且有:

上述模型稱為二步Markov模型,它的核心任務是建立一個與一階Markov模型的轉移概率矩陣同規模的轉移概率矩陣。矩陣的行元素代表用戶瀏覽的上一個網頁,列元素代表用戶下一步可能瀏覽的網頁。通過該矩陣可以根據用戶上一步瀏覽的網頁來預測下一步要瀏覽的網頁。

在多Markov模型方面,劉業政等提出可變多階Markov鏈模型VMOMC。VMOMC將用推薦目標網頁概率值度量的可變多階Markov鏈并行組合,組合模型中采用遺傳算法確定各單階Markov鏈模型的最優權重。陳佳提出了基于混合模型的一種挖掘用戶群在頁面上興趣分布程度的模式發現,計算用戶群從一個頁面到另外一個頁面的導航路徑模式的概率大小,可得到大量的用戶對所訪問Web的興趣及導航模式,從而預測用戶的瀏覽路徑。
2.4 結構相關性模型
有研究表明,用戶在進行Web瀏覽的絕大部分時間里都是從當前頁面中挑選一個鏈接繼續瀏覽;在用戶將來訪問的網頁中,46%能在最近3個網頁的鏈接中找到,75%能在所有歷史網頁的鏈接中找到 。因此,可以認為用戶將來的可能請求大部分存在于由當前頁面上所有鏈接組成的集合中。基于結構相關性的一階Markov模型包括以下三部分:

通過遍歷用戶訪問序列的節點,可以得到用戶的狀態空間和轉移情況,并最終建立上述模型。
結合頁面內容及站點結構來調整狀態轉移矩陣,以獲得更精確的預取結果,提高Web 服務的質量。而利用頻繁訪問模式樹存儲Markov鏈,能夠大幅減小存儲空間。
3 進一步研究的問題
盡管現有的Markov 瀏覽預測模型在預測準確率、覆蓋率方面已取得較滿意的成果,但瀏覽預測問題的實際應用背景中的一些特殊要求使得這一領域仍存在一些需要進一步研究的問題。這些問題包括:
(1)Markov轉移概率矩陣的處理。該模型的存儲空間主要用于保存狀態轉移概率矩陣,所以其存儲空間的復雜度是網頁數目n的平方,即為0(n)。由于n的值一般都比較大,存儲復雜率較高。同時為了提高Web預取的命中率,常常聯合多個Markov鏈模型,即用到了多階狀態轉移矩陣,使得存儲復雜率成倍提高。因此如何存儲及處理Markov模型的概率矩陣、降低復雜度是急需解決的問題。此外,在很多情況下狀態轉移矩陣是稀疏矩陣,采用什么樣的數據結構來存儲這樣的矩陣也是需要研究的課題。
(2)混合Markov模型的求解問題。混合Markov模型在預測用戶的瀏覽行為方面越來越受到學者的重視。有效的模型求解方法,能大大提高模型的效率。雖有學者進行了有益的探索,但這方面的工作仍需要更多學者的參與。
(3)在實際瀏覽預測問題中,Markov的隨機統計方法與其他方法,如神經網絡、貝葉斯網絡、聚類、關聯規則、遺傳算法等相結合能獲得較高的預測準確率。
(4)用戶在Web空間的瀏覽過程是一個受瀏覽目的、
文化背景、興趣愛好等多種因素影響的復雜動態過程,如能有效地度量用戶的瀏覽興趣,并及時發現用戶的興趣遷移,對于提高預測準確率非常重要。此外,隨著無線網絡的普及,怎樣預測無線網絡環境下用戶的瀏覽行為,是研究人員面臨的又一個課題。
全文概述了基于Markov的各種預測模型,分析了各個模型的原理及優缺點,指出了今后的研究方向。
-
神經網絡
+關注
關注
42文章
4775瀏覽量
100917 -
瀏覽器
+關注
關注
1文章
1032瀏覽量
35412 -
網頁
+關注
關注
0文章
73瀏覽量
19342
發布評論請先 登錄
相關推薦
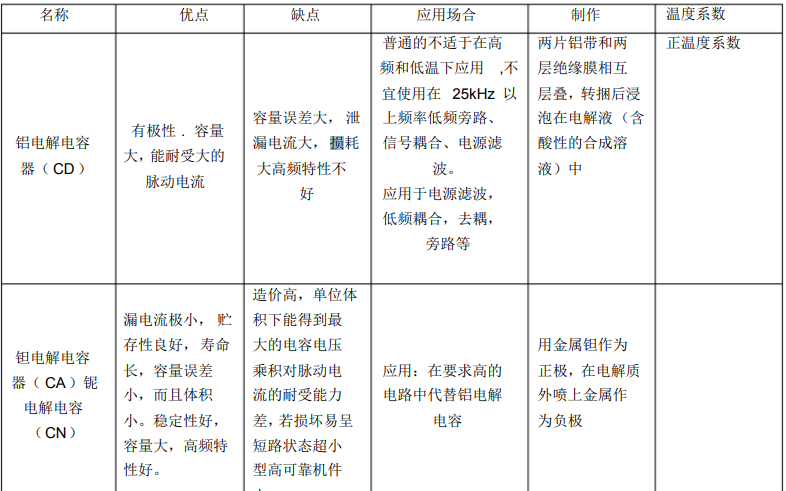
天線各種材質的優缺點
衛星信道三狀態Markov模型設計
如何使用Adaboost Markov模型進行移動用戶位置預測方法的詳細資料說明




 Markov的各種預測模型的原理與優缺點介紹
Markov的各種預測模型的原理與優缺點介紹










評論