隨動系統servo system,是一種反饋控制系統。在這種系統中,輸出量是機械位移、速度或者加速度。因此隨動系統這一術語,與位置或速度,或加速度控制系統是同義語。在隨動系統中,有一類,它的參考輸入不是時間的解析函數,如何變化事先并不知道(隨著時間任意變化)。控制系統的任務是在各種情況下保證輸出以一定精度跟隨著參考輸入的變化而變化。bang-bang控制在系統偏差大,可加大系統的控制力度,提高系統的快速性,因此,bang-bang控制是隨動系統中不可缺少的控制方式。
bang-bang控制理論
bang-bang控制方面的研究始于20世紀50年代。在過去的20年中,魯棒控制一直是國際自控界的研究熱點。所謂“魯棒性”,是指控制系統在一定(結構,大小)的參數攝動下,維持某些性能的特性。根據對性能的不同定義,可分為穩定魯棒性和性能魯棒性。以閉環系統的魯棒性作為目標設計得到的固定控制器稱為魯棒控制器。由于工作狀況變動、外部干擾以及建模誤差的緣故,實際工業過程的精確模型很難得到,而系統的各種故障也將導致模型的不確定性,因此可以說模型的不確定性在控制系統中廣泛存在。
bang-bang控制最早由龐特里亞金提出。在移動目標集的時間最優控制問題中,已知受控系統的狀態方程為x(t)=f(x(t),t)+b(x(t),t)u(t),假設f(x(t),t)和b(x(t),t)的元對x(t)和t是連續可微的。r維容許控制向量u(t)的約束條件為|uj(t)|≤1,j=1,2,…,r.從初態x(t0)=x0出發,在某一末態時刻t》t0,首次達到移動目標集g(x(t),t)=0.其中g是p維向量函數,其各元對x(t)和t是連續可微的,同時性能指標j[u(。)]=∫dt t-t0為最小[6,7]。最優控制u(f)應滿足。
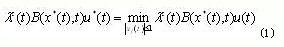
且=f(x(t),t)+b(x(t),t)u(t) (2)
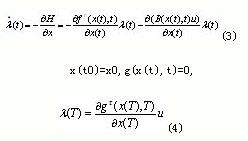
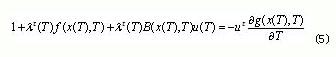
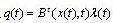
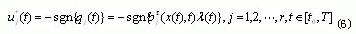
即時間最優控制的各個分量u(t)都是時間t的分段常值函數,并在開關時間上由一個恒值到另一個恒值的跳變。
bang-bang控制在隨動系統中的具體應用
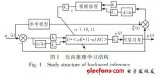
現代魯棒控制是一個著重控制算法可靠性研究的控制器設計方法。其設計目標是找到在實際環境中為保證安全要求控制系統最小必須滿足的要求。一旦設計好這個控制器,它的參數不能改變而且控制性能能夠保證。魯棒控制方法,是對時間域或頻率域來說,一般要假設過程動態特性的信息和它的變化范圍。一些算法不需要精確的過程模型,但需要一些離線辨識。一般魯棒控制系統的設計是以一些最差的情況為基礎,因此一般系統并不工作在最優狀態。常用的設計方法有:INA方法,同時鎮定,完整性控制器設計,魯棒控制,魯棒PID控制以及魯棒極點配置,魯棒觀測器等。
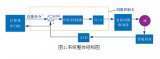
在隨動系統需要進行調轉運動時,在某點需要以最大可能的加速度εm進行回歸,此時誤差|em|≥emax當到達某點時,又需要以-εm進行減速,當速度減到零時,誤差也恰好為零,這就需要通過bang-bang控制來完成[2][3][4][5]。如圖1的bang-bang控制閾值曲線。
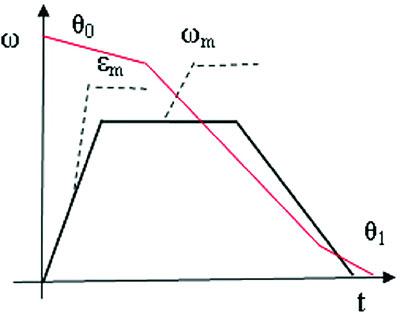
圖1bang-bang控制閾值曲線
圖1中粗線表示速度變化曲線,細實線表示誤差角變化曲線。當某一起點誤差較大時,控制系統以最大可能的加速度εm進行加速,到達θ0點時以最大速度運行,當到達θ1點時以最大加速度-εm進行制動。當速度減到零時,其誤差恰好等于零。這是理想的最快的調轉過程。要達到上述的要求就要正確判定轉換點θ1,通常可以認為伺服電機的扭矩為恒定的,同時不考慮負載阻力矩的變化,系統可以看作為恒加速系統,則可以計算出開始制動時刻的誤差角:
單片機收到電流反饋信號,經過bang-bang控制等智能協調處理得出輸出控制量,根據輸出量的大小確定pwm的占空比。主控制芯片選用intel公司的87c1961mc芯片,其自有的p1、p2、p3、p4口完全能滿足控制需要。系統硬件簡圖如圖2.
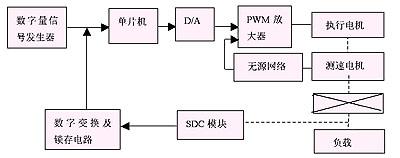
圖2系統硬件簡圖
軟件實現
上面分析轉換點和控制閾值都是理想的情況,實際上系統制動加速度εm的大小取決于電機的扭矩和負載的特性(阻力矩、轉動慣量等參數)。控制程序內采用bang-bang算法設定的加速度大小應與負載實際加速度大小相對應,否則就會出現二次啟動或超調過大現象,影響到系統性能。當控制程序內的制動加速度εm的值設定較小時,計算出來的制動角與實際的相比就會偏大,就會出現制動過早現象,即制動已經結束(速度已經降到零),但系統還沒有到達預定位置,此時系統就會重新啟動,這就是二次啟動問題。這會造成調轉時間過長,影響到系統的快速性。同時,當控制程序內的制動加速度εm的值設定較大時,計算出來的制動角與實際的相比就會偏小,就會出現制動過晚現象,即系統已經到達預定位置,但制動還沒有結束(速度還沒有降到零),此時系統出現超調。較小的超調是正常的,在負載上基本沒有反映;超調很大時,機械負載就會有反映,即出現回擺現象,同時也會造成調轉時間過長,影響到系統的快速性。出現二次啟動或超調過大現象時,只需改動控制程序中的加速度參數即可解決。
系統進行調轉控制程序流程圖如圖3.
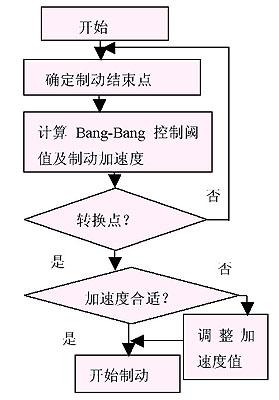
圖3調轉控制程序流程圖
系統仿真
通過采樣出的點,能繪出系統在進行不同階躍運動時的曲線。同時,對系統進行仿真,能得出在正常制動、超調過大和二次啟動的曲線,與采樣出的曲線比較,相同運動狀態下曲線基本吻合。具體仿真曲線如圖4~6.

圖4 二次啟動簡圖圖5 回擺現象簡圖圖 6 正常制動簡圖
結語
仿真結果說明,bang-bang控制在隨動系統調轉控制能很好滿足系統快速性的要求,達到階躍過程最小化,并且結合其它控制方法能提高系統自適應能力和控制精度,有很好的推廣價值。
-
控制系統
+關注
關注
41文章
6637瀏覽量
110692 -
智能
+關注
關注
8文章
1712瀏覽量
117585 -
設計
+關注
關注
4文章
818瀏覽量
69911
發布評論請先 登錄
相關推薦
{:1:}推薦一種設計流程,它在電機控制設計中利用了 Altera FPGA 強大的適應能力
控制板的電源突變適應能力試驗
FPGA在電機控制系統設計中有哪些應用?
采用bang-bang PD的CDR電路設計常見問題解答
基于自適應PID控制的多孔陶瓷透氣度測試系統的設計
神經網絡在PLC控制系統中的應用
PID控制在交流位置伺服系統中的應用




 Bang-Bang控制在隨動系統中能提高系統自適應能力和控制精度
Bang-Bang控制在隨動系統中能提高系統自適應能力和控制精度












評論