小伙伴們有沒有好奇,數據在計算機內存中,是如何存儲的?計算機中物理內存的模型是怎樣的呢?今天大雄就給大家詳細的介紹一下。
在了解存儲模型之前,我們首先應該了解一下計算機的存儲體系。
個人感覺學這部分的知識應該首先在腦海中抽象出存儲體系,因為無論磁盤,物理內存還是虛擬內存都是互相有聯系的,抽象出模型有助于我們的理解和記憶。接著需要哪部分知識或再次深入哪部分知識,從體系圖中找。
建議不要在這塊知識拉長戰線,看了前面忘后面。
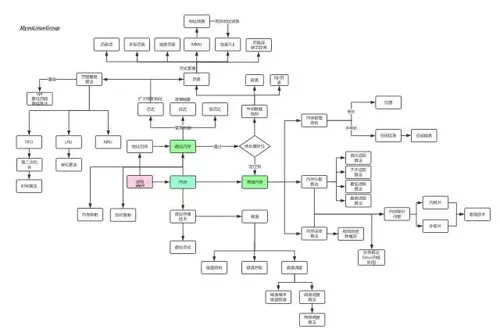
計算機存儲體系圖
簡述上圖:
從進程開始,我們知道進程運行在內存中,每個進程都有自己獨立的內存地址空間,目的是安全和高效利用內存,一個進程的地址空間是抽象出來的,屬于虛擬內存,而內存分為虛擬內存和物理內存。
從物理內存分析,物理內存管理分為等長和不等長劃分,等長劃分一般通過位圖來記錄結構,不等長劃分一般通過空閑區表來記錄。
而物理內存的要通過算法來使進程合理分配回收,其中分配算法有四種,回收算法分為四種情況,而內存分配和回收會引起內存碎片問題,內存碎片問題分為內碎片和外碎片,解決方案有壓縮技術。
從虛擬內存分析,分為頁式/段式/段頁式內存管理,中間通過頁表/段表/段頁表來進行物理到虛擬內存的轉換,重點是頁式管理,頁式管理中重要的概念有頁表項,多級頁表,倒排頁表,MMU,快表TLB和頁錯誤/缺頁異常,而虛擬存儲技術中核心概念就是將內存中暫時不用的頁面(內存塊)放入磁盤上,問題是哪些頁面(內存塊)放到磁盤上呢,于是我們引入頁面置換算法,其中OPT為理想置換算法,基本算法有FIFO,FIFO改進后的第二次機會算法和時鐘算法,LRU中老化算法和NRU,既然部分頁面暫存到磁盤上,那么就要聊聊磁盤。
磁盤是硬件,所以要討論它的結構,和如何存取數據,以及磁盤調度的一些算法,此外,虛擬內存還有重要的兩個技術就是內存映射和寫時復制。
物理內存
物理內存其實就是我們機器的實際內存大小,比如我的筆記本電腦內存是4G。我們都知道程序是要加載道內存中才能執行,所以物理內存越大,我們電腦的性能就越好。
位圖
位圖(bitmap),其實就是用位來標記數據。
在等長內存管理中,比如我們將內存等分為大小相同的內存塊,那么一位標記一塊,因為會形成一個位圖。
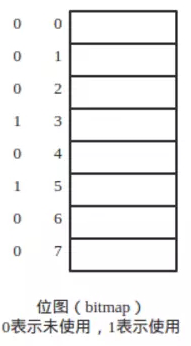
這樣,我們需要多大的塊,只需要匹配bitmap中連續多少個0即可。
空閑區表
在不等長劃分中,比如我們根據進程的大小來分配內存,這是就需要采用空閑區表來存儲空閑的內存。
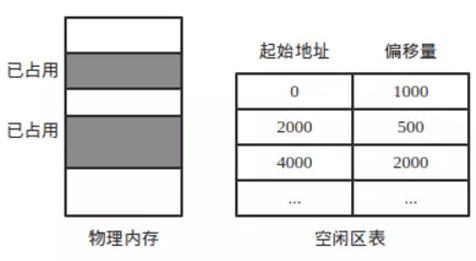
空閑區鏈表只不過是通過鏈式結構將空閑區表中的數據組織起來。
內存分配算法
上面說了我們如何通過數據結構來組織未分配的內存,我們以空閑區鏈表結構為例,下面來說說物理內存的分配算法,有如下四種。
1.首次適配算法
首次適配算法是在空閑區鏈表中從頭開始查找符合申請內存大小的塊,直到找到滿足條件的為止,該算法不斷的從頭開始試驗申請,所以大部分使用的都是低地址空間的內容,從而流出了高地址空間來滿足大的申請需求,但是缺點是會在較低的地址空間中頻繁的申請和釋放導致低地址空間中的內存碎片,而且每次都查找都從頭開始,查找效率比較低。
2.下次適配算法
下次適配算法是首次適配算法的一個改進,它每次從上一次適配的地方開始向下查找,不需要每次都從頭開始,此算法使得內存使用均勻,但是不會有大的內存塊來滿足內存分配。
3.最佳適配算法
此算法先按照內存塊的空閑區大小從小到大進行排序,排序后,每次從頭開始匹配,這樣匹配出來的結果肯定是最優的,但實際因為比較符合申請內存的大小,會出現很多較小的內存碎片無法使用,并且每次分配后都要重新排序,開銷比較大。
4.最差適配算法
此算法按照內存塊的空閑區從大到小進程排序,排序后,有進程申請內存時,將表頭最大的內存塊分配給它,這樣如果不能分配則所有不能分配,且將大內存分配給它,若只占用一小部分還可以進行二次分配。
內存回收算法
內存分配且進程使用完后,我們要進行回收,一般而言,內存回收算法和內存的分配算法有著密切的關系。
所以我們僅僅看內存回收算法可能會出現的四種情況。
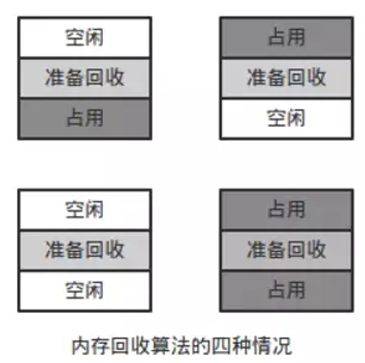
左上為上相鄰,右下相鄰,左下是上下相鄰,右下是上下不相鄰。
內存碎片
什么是內存碎片,就是在內存中占據一定大小的空間卻得不到利用的內存。內存碎片分為內碎片和外碎片。
內碎片:比如按頁式分配等長,那么如果有一個進程需要5頁多內存,那么我們只能給他分配6頁內存,那么這第6頁是未用完的,其中除過一些數據外,我們還有空閑的被該進程占據,其他進程也不能使用。
外碎片:外碎片是還未分出來的,未被進程占用且因為太小或其他不滿足條件再次分配的小的內存塊稱為外碎片。
緊縮技術:我們一般采用緊縮技術來合并小的內存碎片,原理是將暫時不運行的進程安全的移動位置,獨立出內存碎片,從而組裝多個內存碎片合并成一個大的內存塊。
注意的是有些進程并不能被移動,比如正在讀寫IO。
伙伴算法
伙伴算法是Linux底層內存分配回收算法的一種實現。本文只講述伙伴算法的基本原理。
伙伴算法基本思想:
將內存大小變為二的n此方 。
如果一個程序申請的內存塊大小 m 滿足 2^n-1 < m < 2^n條件,那么就將此時的內存塊分配給它。
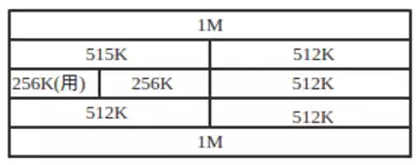
如上圖,我們現在需要200K空間,1M等于1024K,如果m小于1M的一半,那么繼續分離m,當分離到256時,剛好能滿足200K的需求,所以分配。
歸還時,采用內存回收算法的思想,看左右相鄰。若沒被占用則合并(也是為什么叫伙伴算法)。
-
內存
+關注
關注
8文章
3028瀏覽量
74076 -
磁盤
+關注
關注
1文章
379瀏覽量
25209
原文標題:淺談計算機中的存儲模型之物理內存
文章出處:【微信號:cunchujie,微信公眾號:存儲界】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 淺析計算機中物理內存的模型
淺析計算機中物理內存的模型










評論