在混合信號應用中,正確地選擇驅動模數轉換器 (ADC) 的運算放大器至關重要。設計人員 必須要對一些問題進行權衡,例如:放大器噪聲、帶寬、設置時間、ADC 信噪比 (SNR) 的 壓擺率、無雜散動態范圍 (SFDR)、輸入阻抗以及采樣時間等等。本文專門對單電源環境中 噪聲規范和運算放大器以及逐次逼近寄存器 (SAR) ADC 性能的匹配進行了論述。 放大器產生的噪聲源自于輸入差動級。每一個放大器的輸入級都會產生晶體管器件噪聲, 其點噪聲曲線圖描述了參考輸入端 (RTI) 噪聲。利用這一圖形信息,通過計算出參考輸出 端 (RTO) 放大器噪聲我們就可以確定 ADC 輸入端產生了多少噪聲。
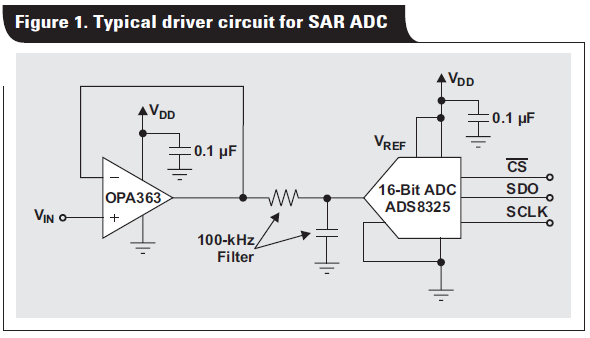
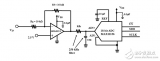
該討論首先從對放大器器件噪聲的描述開始。隨后,將放大器噪聲源和一個性能系數聯系 在一起,同時將一些單位從伏特轉換為以分貝表示的 SNR。最終,通過計算出運算放大器 SNR 值與 ADC SNR 性能的組合值就可以得出該混合信號電路(請參見圖 1)中運算放大器 所產生的影響。
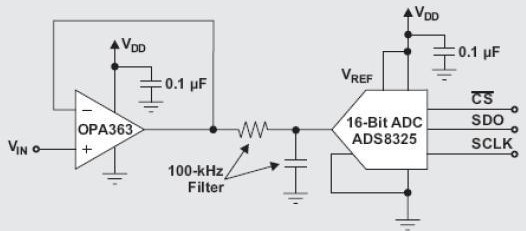
放大器噪聲的特點
了解本應用中運算放大器產生的噪聲是非常重要的。放大器的產品說明書中給出的典型性 能顯示,運算放大器的過頻率噪聲性能具有明顯的特征(請參見圖 2)。本文中,由于我們 考慮到使用單電源 CMOS 放大器的一些影響,因此輸入電流噪聲非常低,以至于我們可以 將其忽略不計。這里,我們將只考慮放大器電壓噪聲的影響。
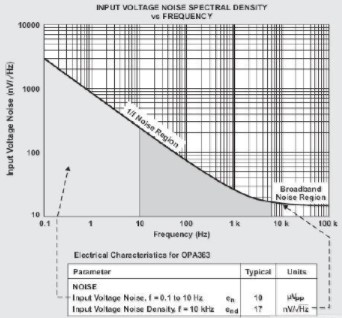
在典型的放大器產品說明書中,放大器噪聲規范為一種 RTI 規范。我們可以在放大器的非 反相輸入端將放大器噪聲量化為一個電壓源。運算放大器的電氣特征表給出了輸入電壓噪 聲和輸入電壓噪聲密度規范(請參見圖 2)。輸入電壓噪聲規范 (10μVPP) 在帶寬方面對 放大器的低頻噪聲作了描述。該帶寬是放大器 1/f 噪聲區域的一個組成部分。放大器輸入 級中的晶體管以及輸入級有源負載共同產生了這種噪聲。
輸入電壓噪聲密度會引起一個頻率的噪聲系數。例如,圖 2 中的電氣特征表顯示,在 10 kHz 下的輸入電壓噪聲密度 (end) 為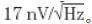 通常,該規范出現在頻率曲線的寬帶噪 聲部分(請參見圖 2)。從理論上來講,這種寬帶噪聲是平坦的。假設是這種情況,那么 平坦噪聲就是對放大器性能的一種較好的*價。不管是擴散電阻器還是晶體管的源極和漏 極,運算放大器中的電阻器都是主要的寬帶噪聲源。
通常,該規范出現在頻率曲線的寬帶噪 聲部分(請參見圖 2)。從理論上來講,這種寬帶噪聲是平坦的。假設是這種情況,那么 平坦噪聲就是對放大器性能的一種較好的*價。不管是擴散電阻器還是晶體管的源極和漏 極,運算放大器中的電阻器都是主要的寬帶噪聲源。
放大器說明書包含了一個典型的規范圖表,其顯示了輸入電壓噪聲密度與頻率的對應關系。 圖 2 就是這類圖表的一個例子。在本例中,輸入電壓噪聲規范就是輸入電壓(即 0.1Hz 至 10 Hz 規定頻率之間的噪聲密度曲線)以下的區域。需要注意的是,該規范的單位為峰至 峰值。為了將其轉換為一個 rms 值,只需將峰至峰值除以 6.6(業界標準峰值因數 [CF] =3.3)即可。
表 1 包含了用于將 rms 轉換為峰至峰值(反之亦然)的典型 CF 值。為了估計峰至峰運 算放大器輸出噪聲電壓,我們將 rms 輸出電壓乘以 2CF。為了估計 ADC 峰至峰輸出比特 性能,可從 rms 規范中減去比特峰值因數 (BCF)。
表 1 用于將 rms 轉換為峰至峰的峰值因數和比特峰值因數值
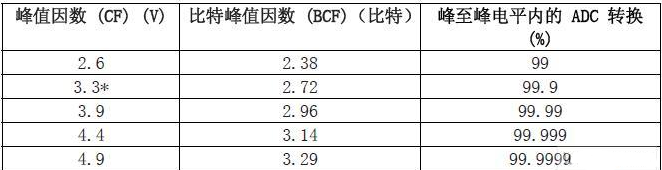
*業界標準的峰值因數
如圖 2,我們可以非常容易地計算出中曲線以下部分,1/f 區域中不同輸入電壓噪聲帶寬 的噪聲。在這一計算過程中,首先要確定 1 Hz 時的輸入噪聲密度。一旦我們得出該值, 下面簡單的公式便會給出曲線以下的 rms 噪聲。

我們在考慮這些低頻噪聲的時候,可能會立即得出這樣的結論:我們應該將這種公式用到 非常低的頻率中,例如:0.0001 Hz (0.0001 Hz = 每 2.8 小時 1 個周期)。但是,在 低于 0.1 Hz 的頻率下,則每 10 秒鐘一個周期,在電路中極有可能會出現其他情況,例 如:溫度、老化程度或組件壽命等發生變化。實際上,來自放大器的低頻噪聲可能不會出 現在這種采樣速度下,但是電路中可能會出現一些變化(例如:溫度或者電源電壓等的變 化)。放大器規范表(請參見圖 2)還給出了輸入噪聲密度值。該規范始終工作在較高的頻率下, 即在輸入電壓噪聲相對穩定的區域中。就這一曲線區域而言,乘以帶寬的平方根和噪聲密 度使噪聲穿過該帶寬。
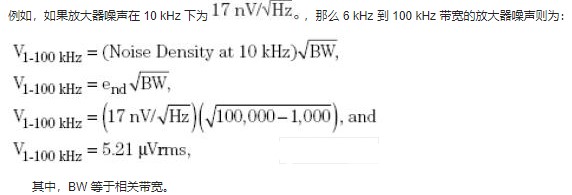
那么,我們如何從廠商的圖表中得到一個 RTO 噪聲值呢?我們可以計算出噪聲曲線以下部 分的面積,然后乘以放大器的噪聲增益。本例中,電路的噪聲增益為+1 V/V。我們首先確 定放大器在兩個區域中的噪聲,然后使用平方和的平方根將這兩個值加起來。圖 3 顯示了 進行這一計算的公式,并闡明了這兩個區域。
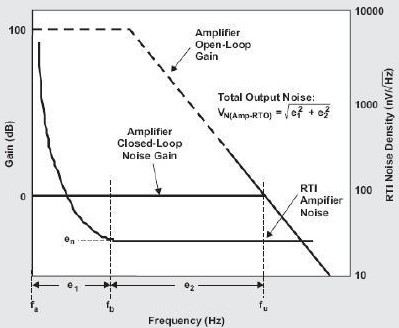
圖 3 將噪聲分為兩部分。在區域 e1 中,通過放大器電路的 dc 增益,我們得到了值為 +1 V/V 的放大器 1/f 噪聲。放大器噪聲的這些規范為幾納伏/赫茲平方根。因此,只有當將 那個區域的帶寬平方根乘以這個區域的平均噪聲時,該分析才算完成。就 CMOS 放大器而 言,1/f 區域通常為從 0.1 Hz 至 100 Hz,甚至可以高達 1000 Hz。由于這一噪聲值被帶 寬平方根相乘,因此其產生的噪聲較低。在區域 e2 中,放大器的寬帶噪聲被放大器電路增益(還是 +1 V/V)和帶寬平方根相乘。

利用 TI 的 SPICE 仿真工具 TINA-TITM,我們可以驗證這一噪聲計算的正確性。請登錄www.ti.com.cn/amplifier 查找該工具。
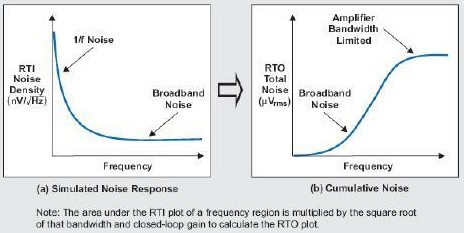
圖 4 中的兩個曲線圖展示了 TINA-TI 如何幫助我們了解電路中的噪聲。圖 4 (a) 顯示了 一個放大器的仿真噪聲響應。圖4 (b) 顯示了頻率增加時的累積噪聲。需要注意的是,在 圖 4 (b) 中,該噪聲在較低頻率下時非常低,這是因為,較低帶寬被一個小數(即帶寬) 的平方根相乘。當頻率增加時,累積噪聲也隨之增加。有人會認為,由于圖 4 (a) 的特點, 在較高頻率下噪聲的增加會更少。正如我們所看到的一樣,并非如此,因為帶寬乘法器(帶 寬的平方根)在高頻時更大。
將運算放大器與 ADC 噪聲系數組合
我們檢查放大器可能存在的噪聲源時,可以較為容易地估計出圖 1 中系統的總噪聲。該系 統使用 16 位 ADC,即 ADS8325,其最大采樣率為 100 ksps。這種器件的典型 SNR 為 91正如我們之前所看到的那樣,OPA363 RTO 噪聲為 109.8 dB。現在,通過使用運算放大器 SNR 和 ADC SNR,并運用平方和的平方根法則,我們就可以確定該系統的總體噪聲了。
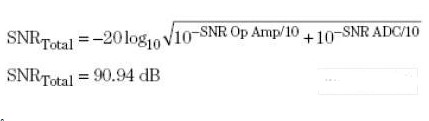
從這一計算,我們可以看到放大器噪聲對系統精度具有非常小的影響。
利用電路中的這些器件,SNR 性能將總是等于或者小于最低值。假定在放大器和 ADC 之間 存在這種相互關系,那么選擇一個更高噪聲的放大器將得到最差的結果。例如,如果我們 使用一個 10 V/V 增益的放大器,其在 10 kHz 下的典型電壓噪聲規范, 那么 SNRTotal 為 82.2 dB。如果我們使用 16 位 ADS8325,那么 SNRTotal 則為 81.6 dB。在 本例中,放大器決定了電路噪聲的高低。
還有更多影響放大器選擇過程的因素,但是放大器噪聲能夠對數字編碼結果產生巨大的影 響。如果放大器的噪聲太大,那么 ADC 肯定會將放大器電路的噪聲轉換成數字輸出。另一 方面,ADC 可能會比放大器電路的噪聲更大。如果我們在沒有*估系統的情況下選擇一款 噪聲極低的放大器,那么我們可能會在一個組件或者其他組件上花費太多的資金。確定一 個電路中潛在的噪聲一直都是一個巨大的挑戰,但是有一些經驗法則是可以被用來克服這 些問題的。基于我們在計算方面的優勢,我們可以利用電路的頻率范圍;另外,當我們組 合噪聲源時,我們可以利用這一方程式來對平方和的平方根求解。通過使用這些技巧,我 們可以迅速地確定放大器/ADC 組合的一致性。
在本電路中,一個放大器將信號鏈阻抗隔離。我們可以添加其他一些特性,例如:增益或 濾波;但是無論我們在放大器周圍添加了什么特性,我們都應該始終確保放大器電路能夠 保持 ADC 的完整性。
-
噪聲
+關注
關注
13文章
1134瀏覽量
47678 -
運算放大器
+關注
關注
215文章
5160瀏覽量
174566 -
模數轉換器
+關注
關注
26文章
3252瀏覽量
127481
發布評論請先 登錄
相關推薦
超精密電阻在運算放大器電路中的應用
基于運算放大器的高精度模數轉換器驅動
意法半導體噪聲最低的高端醫療及儀表專用運算放大器
超精密電阻在運算放大器電路中的應用
超精密電阻在運算放大器電路中的應用
運算放大器的噪聲性能與ADC相匹配
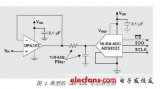
高速運算放大器和模數轉換器電路新的計算分析方法
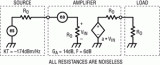
運算放大器和逐次逼近寄存器的噪聲性能與ADC性能的匹配詳細概述



















評論