摘 要：研究了具有不確定參數(shù)非線性系統(tǒng)的穩(wěn)定最優(yōu)模糊保代價(jià)控制問題。采用T-S模糊模型描述非線性系統(tǒng)，對(duì)具有范數(shù)有界，時(shí)變參數(shù)不確定性的非線性系統(tǒng)，得到了存在穩(wěn)定最優(yōu)模糊保代價(jià)控制器的充分條件，并推算出了相應(yīng)的線性矩陣不等式（LMI）形式。建立了永磁同步電動(dòng)機(jī)混沌系統(tǒng)的T-S模型，采用最優(yōu)模糊保代價(jià)控制器進(jìn)行控制，針對(duì)不含參數(shù)不確定性和含有參數(shù)不確定性兩種情況進(jìn)行仿真研究，均得到滿意的控制效果。

1 引言

混沌控制是當(dāng)前混沌運(yùn)動(dòng)研究的一個(gè)新領(lǐng)域。是實(shí)現(xiàn)混沌應(yīng)用的關(guān)鍵環(huán)節(jié)。多年來，人們對(duì)混沌運(yùn)動(dòng)的性質(zhì)產(chǎn)生了一些廣為接受的認(rèn)識(shí)，即混沌軌道的長期趨勢是不可預(yù)言的，并且混沌運(yùn)動(dòng)是難以控制的。1990年E.Ott、C.Grebogi和J.A.Yorke提出控制混沌的思想（OGY控制）產(chǎn)生廣泛影響。以后十年，新的研究成果不斷涌現(xiàn)。以上方案無須改變系統(tǒng)固有參數(shù)，即可實(shí)現(xiàn)對(duì)混沌系統(tǒng)的有效控制，但是，要求系統(tǒng)參數(shù)是定常的。當(dāng)混沌系統(tǒng)具有不確定參數(shù)時(shí)，以上方案將失效。近年來，關(guān)于不確定參數(shù)的混沌系統(tǒng)的控制已引起重視。電力系統(tǒng)中存在著許多混沌現(xiàn)象。其中永磁同步電動(dòng)機(jī)的數(shù)學(xué)模型是多變量、強(qiáng)耦合的非線性系統(tǒng)，能呈現(xiàn)出非常豐富的動(dòng)態(tài)行為，如極限環(huán)和混沌。對(duì)其如何進(jìn)行控制也是一個(gè)重要的研究課題。

對(duì)于不確定線性系統(tǒng)，基于Riccati方程和線性矩陣不等式（LMI）提出了一系列的魯棒控制器設(shè)計(jì)方法。對(duì)于不確定非線性系統(tǒng)，現(xiàn)有的研究成果還很少。實(shí)踐證明，具有線性后件的T-S模糊模型充分利用局部信息和專家經(jīng)驗(yàn)，能以任意精度逼近實(shí)際的控制對(duì)象。在考慮模型不確定性的情況下，文獻(xiàn)提出了模糊魯棒控制的概念，并取得了一定的成果。本文針對(duì)一類由T-S模糊模型表示的不確定連續(xù)非線性系統(tǒng)，導(dǎo)出了最優(yōu)保代價(jià)控制器存在的充分條件。閉環(huán)系統(tǒng)不但漸近穩(wěn)定，而且性能指標(biāo)小于某一代價(jià)值。采用線性矩陣不等式（LMI）技術(shù)，給出了該控制器的設(shè)計(jì)方法和參數(shù)化表示。并將所得的控制器應(yīng)用到永磁同步電動(dòng)機(jī)混沌系統(tǒng)中，建立了永磁同步電動(dòng)機(jī)混沌系統(tǒng)的T-S模型， 針對(duì)不包含不確定參數(shù)和包含不確定參數(shù)兩種情況，均得到了滿意的控制效果。

2 問題的描述

在系統(tǒng)局部信息或?qū)＜医?jīng)驗(yàn)存在的條件下，不確定非線性連續(xù)系統(tǒng)可以采用如下i條規(guī)則的T-S模糊模型進(jìn)行描述：

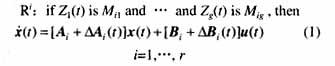
式中 Ri表示T-S模糊模型的第i條規(guī)則，也稱為模糊子系統(tǒng)；Z1（t），…， Zg（t）為模糊規(guī)則的前件變量；Mij為模糊語言集合；x（t）∈Rn， u（t）∈Rm分別為系統(tǒng)的狀態(tài)變量和控制變量；Ai， Bi是適當(dāng)維數(shù)的實(shí)常數(shù)矩陣，DAi（t）， DBi（t）是不確定矩陣，他們反映了系統(tǒng)模型中的時(shí)變參數(shù)不確定性。

本文考慮的不確定性假設(shè)是范數(shù)有界的且有如下結(jié)構(gòu)：

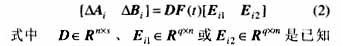
的具有適當(dāng)維數(shù)的常數(shù)矩陣，它們反映了系統(tǒng)不確定性的結(jié)構(gòu)，F(xiàn)（t）∈Rs×q是具有Lebesgue可測元的不確定矩陣，且滿足FT（t）F（t）≤I。

上述不確定性的結(jié)構(gòu)假定并不失一般性。首先，它可以表示一個(gè)含有裝置和不確定性F（t）的線性關(guān)聯(lián)的系統(tǒng)；其次，有許多系統(tǒng)，其不確定性可以按這種方式表示，例如，滿足“匹配條件”的不確定性就可以解釋成是通過輸入進(jìn)入到系統(tǒng)模型中的，即D為系統(tǒng)的輸入矩陣；最后對(duì)一般的范數(shù)有界不確定性，總可以選擇適當(dāng)?shù)慕Y(jié)構(gòu)矩陣，使其具有上面的形式。

采用文獻(xiàn)中的單點(diǎn)模糊產(chǎn)生器，乘積推理以及加權(quán)平均模糊消除器，上述的模糊邏輯控制系統(tǒng)可寫為如下形式中。

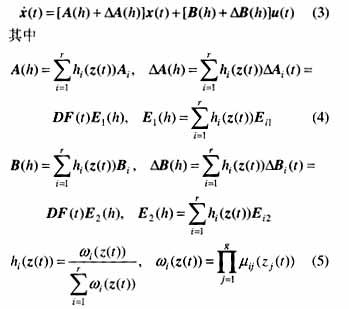
3 最優(yōu)保代價(jià)控制

首先給出保代價(jià)控制的定義，然后給出模糊不確定系統(tǒng)（3）的穩(wěn)定保代價(jià)控制器存在條件。在此基礎(chǔ)上利用線性矩陣不等式給出控制器的設(shè)計(jì)方法。

定義1（保代價(jià)控制）考慮不確定系統(tǒng)（3），如果存在控制律u*（t）和正標(biāo)量J*，使得對(duì)所有允許的不確定性FT（t）F（t）≤I，閉環(huán)系統(tǒng)是穩(wěn)定的，且代價(jià)函數(shù)（9）對(duì)此閉環(huán)系統(tǒng)滿足J≤J*，則稱J*是一個(gè)保代價(jià)，而稱u*（t）是不確定系統(tǒng)（3）的保代價(jià)控制律。

下面給出不確定系統(tǒng)（3）狀態(tài)反饋保代價(jià)控制律存在的一個(gè)充分條件。

定理1式（7）的反饋控制律是一個(gè)保代價(jià)控制律，如果存在公共正定矩陣P∈Rn×n和矩陣k（h），使得對(duì)任意允許的不確定性F（t），有如下矩陣不等式

設(shè)存在對(duì)稱陣P》0使得矩陣不等式（10）對(duì)所有允許的不確定性成立。定義Lyapunov函數(shù)為

因此，由Lyapunov穩(wěn)定性理論，閉環(huán)模糊系統(tǒng)（11）是漸近穩(wěn)定的。

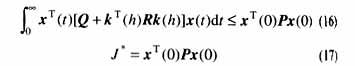
由定義1知定理1的結(jié)論成立。

下面將證明，上述推導(dǎo)的存在控制器使全局模糊系統(tǒng)漸近穩(wěn)定的充分條件，可等價(jià)于線性矩陣不等式的可解性。

定理2 對(duì)于系統(tǒng)（11），存在對(duì)稱正定矩陣P使不等式（10）成立，當(dāng)且僅當(dāng)存在一標(biāo)量e 》0，正定對(duì)稱矩陣X∈Rn×n和矩陣W（h）∈Rm×n滿足如下矩陣不等式

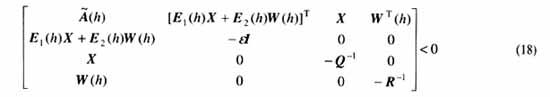
那么式（10）可被寫成式（22）

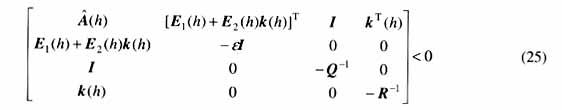
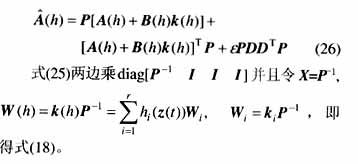
定理3 給定系統(tǒng)（1），存在保代價(jià)控制律（19）的條件是，存在公共正定矩陣X和矩陣Wj及標(biāo)量e，滿足如下線性矩陣不等式

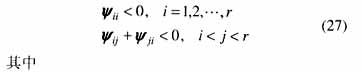
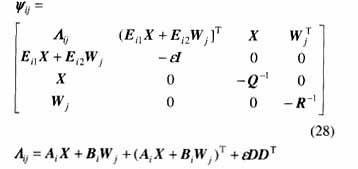
證明：由不等式（18）和式（4）可知，不等式（18）左邊等于

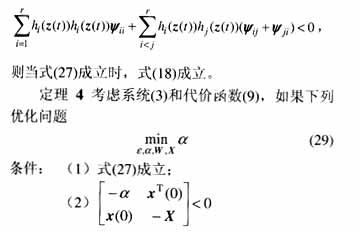
有解ε，α，W，X，則式（19）的控制律是一個(gè)無記憶狀態(tài)反饋控制律，它使得不確定系統(tǒng)（3）的代價(jià)函數(shù)的極小值為式（20）。

證明： 根據(jù)定理2，由任意可行解ε，α，W，X所構(gòu)造的控制律（19）是系統(tǒng)（3）的一個(gè)保代價(jià)控制律。由Schur補(bǔ)引理可知，式（29）中的條件（2）等價(jià)于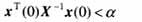

所以，由方程（20）有J*《α。

于是，極小化α隱含極小化不確定系統(tǒng)（3）的代價(jià)函數(shù)。而式（29）中，目標(biāo)函數(shù)和約束條件的凸性，保證了該優(yōu)化問題的最優(yōu)性。

4 永磁同步電動(dòng)機(jī)混沌系統(tǒng)的T-S建模與控制

4.1 T-S建模

將上述控制器應(yīng)用到文獻(xiàn)［5-6］的永磁同步電動(dòng)機(jī)混沌系統(tǒng)。

考慮加上一個(gè)控制項(xiàng)的永磁同步電動(dòng)機(jī)有如下形式的數(shù)學(xué)模型（其原模型見文獻(xiàn)［5-6］）

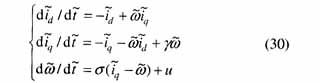
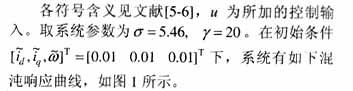
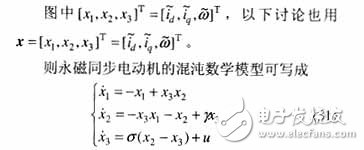
仿文獻(xiàn)的建模過程，對(duì)永磁同步電動(dòng)機(jī)建立T-S模型。將非線性項(xiàng)x3（t）x2（t），x3（t）x1（t）寫成線性函數(shù)加權(quán)和的形式。

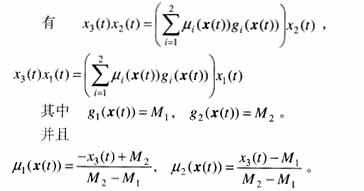
因?yàn)閮煞蔷€性項(xiàng)都是x3的函數(shù)，則可以構(gòu)造如下精確T-S模型。

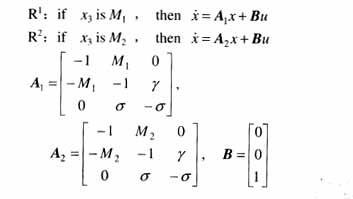
知x3（t）∈［-20，20］，所以選擇M1=-20，M2=20。由推導(dǎo)過程可看出M1，M2是一類特殊的模糊集合，即精確的數(shù)值。是一種精確建模，無建模誤差。

4.2 系統(tǒng)不含不確定參數(shù)時(shí)的最優(yōu)保代價(jià)控制

此時(shí)，DAi（t）， DBi（t）都為0，故D，Ei1，Ei2也都為0。簡單取e=0.1，R=1，Q=I由式（27），（29）得

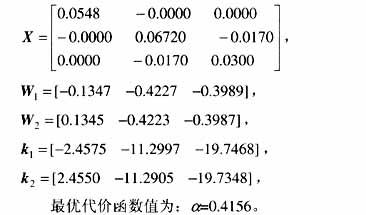
取式（7）的控制律，在初始條件為x0=（0.01 0.01 0.01）T，u=0及在t=60s加入控制項(xiàng)的仿真結(jié)果如圖2所示，可看出加入控制項(xiàng)后系統(tǒng)趨于穩(wěn)定。

4.3 系統(tǒng)包含不確定參數(shù)時(shí)的最優(yōu)保代價(jià)控制

假設(shè)系統(tǒng)參數(shù)g，s 的不確定性在其標(biāo)稱值30%內(nèi)。其不確定性代表參數(shù)攝動(dòng)或建模誤差。在參數(shù)30%攝動(dòng)下，系統(tǒng)仍呈現(xiàn)混沌行為。仿真中每個(gè)參數(shù)加30%隨機(jī)擾動(dòng)，由MATLAB中的rand（ ）隨機(jī)函數(shù)實(shí)現(xiàn)，則有

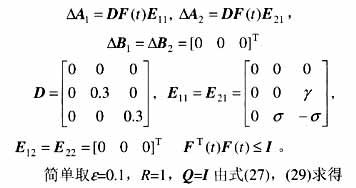
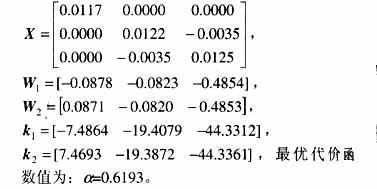
取式（7）的控制律，在初始條件為x0=（0.01 0.01 0.01）T，u=0及在t=60s加入控制項(xiàng)的仿真結(jié)果，可看出加入控制項(xiàng)后，不確定參數(shù)系統(tǒng)趨于穩(wěn)定。

加入控制項(xiàng)實(shí)現(xiàn)了不含參數(shù)不確定性和含有參數(shù)不確定性混沌系統(tǒng)的穩(wěn)定控制。系統(tǒng)狀態(tài)由原來的混沌運(yùn)動(dòng)迅速達(dá)到平衡點(diǎn)。本文的控制方法與OGY法的小信號(hào)輸入法不同，系統(tǒng)狀態(tài)遠(yuǎn)離目標(biāo)狀態(tài)時(shí)，啟動(dòng)控制作用，即可將系統(tǒng)狀態(tài)控制到目標(biāo)狀態(tài)，而與輸入加入的時(shí)刻無關(guān)。

5 結(jié)論

基于T-S模糊模型，給出了存在穩(wěn)定最優(yōu)模糊保代價(jià)控制器的充分條件和相應(yīng)的LMI形式。應(yīng)用到永磁同步電動(dòng)機(jī)混沌系統(tǒng)的穩(wěn)定控制中，建立了永磁同步電動(dòng)機(jī)混沌系統(tǒng)的T-S模型，對(duì)不包含不確定參數(shù)和包含不確定參數(shù)兩種情況，取得了滿意的控制效果。不需要改變被控系統(tǒng)的內(nèi)部結(jié)構(gòu)，具有良好的穩(wěn)定性，且能達(dá)到某一性能指標(biāo)最優(yōu)。