圖1提供了濾波器部分的原理圖,這是本文要討論的主題。
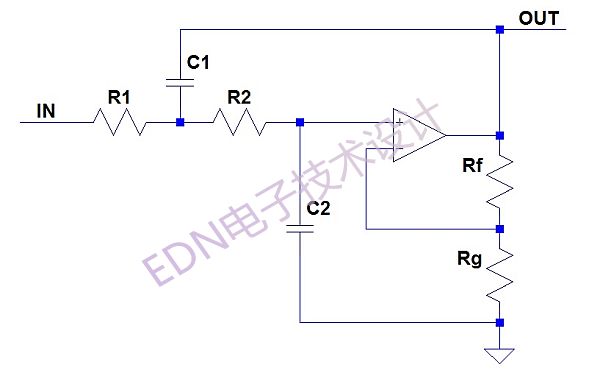
圖1:SallenKey二階低通濾波器原理圖。
網上有許多不同的濾波器設計包。有些要求用戶指定濾波器階數和響應類型,例如Butterworth或Bessel。其它則要求通帶紋波和寬度,以及阻帶衰減,然后自動選擇響應類型。這些可能會針對噪聲、電壓范圍、低功耗或其它參數來優化。
其它設計包提供了更多的靈活性,而不只是處理響應類型,它們可讓用戶指定每個二階濾波器的品質因數Q和諧振頻率ω0(弧度/秒)。它們要求用戶指定額外的參數組合來限定問題。這些參數可能包括DC增益和/或某些元件值。有了這些信息,就可以通過計算確定剩余的值。有時會提到Q和ω0對元件容差的敏感性問題。眾所周知,濾波器在ω0時的幅度響應表現出最大的變化,即使對于合適的Q值也是如此,但是在單位DC增益(Rf/Rg = 0)的情況下,這種變化最小。這就要求C1 = 4·Q2·C2,這對于Q值較大時可能是有問題的。本文介紹的方法是當C1小于4·Q2·C2時,如何讓濾波器響應靈敏度在頻率ω0時達到最小。
濾波器配置的響應由下式給出:
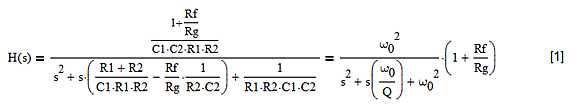
圖2:以Q和ω0值表示的濾波器響應。
為了方便,我們在求解元件值之前先定義一些術語。適用于設計的電容值范圍受到尺寸、價格和容差的限制。因此,我們要控制電容比,也希望控制DC增益,它等于1+Rf/Rg。所以我們定義:

圖3:定義本文公式中將使用的一些術語。
從公式(1)可以看出,真正起作用的是電阻Rf和Rg之比Rr,而不是它們的絕對值。因此,一旦我們指定Rr,就可以選擇數值大的Rf和Rg,以便使功耗最小,或者選擇數值小的Rf和Rg,以便使噪聲最小。如果我們還指定了C1和C2,則Cr也確定了。從這些值可以得出R1和R2:
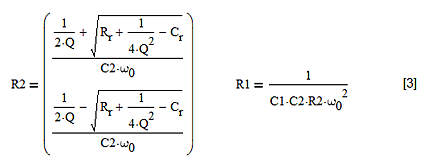
圖4:用C2、Rr、Cr、Q和ω0計算R1和R2的值。有兩組電阻值。
可實現性對Rr和Cr有一些約束要求。為確保平方根項及電阻R1和R2是實數,需要:
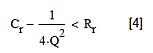
圖5:所有濾波器的實現約束條件。
此外,從1/(2·Q)中減去平方根項的R2的表達式必須是正數,我們將其稱為減法根。另一個稱為加法根。所以,對于減法根,總約束是:
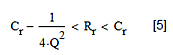
圖6:R2的減法根構成的濾波器的實現約束條件。
公式(5)將R1和R2限制到減法根的一個小范圍的值。稍后我們會看到,我們希望避免使用減法根實現濾波器,因為對于給定的Q、ω0、Cr和Rr,我們總是可以用加法根構建不太敏感的濾波器。
過去的設計中都是計算Q相對于電阻和電容每個值變化的靈敏度。但這里采用的方法是計算在頻率ω0處濾波器響應幅度的靈敏度,ω0是變化最大的頻率。這六個元件中每一個的靈敏度表達如下,其中Rr12=R2/R1:

圖7:諧振時濾波器響應幅度對每個元件值的靈敏度。
找出靈敏度的平方和
下一步是找出這些靈敏度的平方和,這樣就可以得到盡可能小的值。結果(除以2)是:

圖8:諧振時濾波器對每個元件靈敏度的總和(除以2)。Ctol項是電容與電阻容差的比值。
請注意術語Ctol,這是電容容差與電阻容差的比值。例如,2.5%的電容容差和1%的電阻容差會得到2.5的Ctol值。在這種情況下,Ctol解釋了電容值的更大變化。
我們希望確定公式的參數并消除Rr12,它可以用Cr和Rr表示。此外,由公式(3)給出的R1和R2電阻對的兩個根的單獨表達式是很有用的。我們也借此機會切換到平方和的平方根,因為這與所有元件的總靈敏度成正比。最后,我們希望僅繪制元件值的可實現范圍。由于正在使用的圖形包不會在圖中畫出虛數值,因此我們將√(-1)分配給不可實現的濾波器:

圖9:諧振時濾波器響應幅值的每個元件靈敏度的平方和(除以2)的根。它包括R2的加法和減法根表達式。R1和R2用Cr和Rr表示。如前所述,術語Ctol也被采用。
圖10顯示隨Rr變化的各種Cr值的濾波器的靈敏度。所示曲線的Q = 10和Ctol = 2.5,無論C2和ω0的絕對值如何,這些值都是有效的。實線是加法根靈敏度,虛線是減法根靈敏度。對于給定的Cr值,這兩個根的曲線顏色相同。

圖10:被兩部分濾波器分開的總靈敏度曲線,其中Q = 10和Ctol = 2.5,隨著Rr變化,各種Cr值變化導致靈敏度變化。實曲線是加法根靈敏度,虛線是減法根靈敏度。對于給定的Cr值,這兩個根的曲線顏色相同。
從圖中可以清楚看出幾點。首先是給定Cr的加法根的最小靈敏度總是小于相應的減法根的最小靈敏度。因此,我們不應該使用減法根的元件值構建濾波器。第二個觀察結果是,一般來說,Cr = C2/C1的值越小,可以實現的靈敏度就越低(更好)。第三,直覺可能會告訴我們,最好的解決方案是使用最小的Rr值產生可實現的濾波器,但曲線顯示并非這樣。第四,底部的橙色水平實線是我們能達到的最好結果。它對應于單位DC增益,Rf短路和/或Rg開路,并對應于Cr = .25·Q-2,即C1 = 4·Q2·C2。如果我們認為使Cr值更小會進一步降低靈敏度的話,那么直覺再一次失敗。當我們將Cr設為.125·Q-2時,橙色水平實線之上的橙色水平虛線會告訴真相。
我一直無法找到Rr最佳值的閉合解——曲線的鞍點,即對給定的Q、ω0、Cr和Ctol,濾波器的總靈敏度最小的位置。不過我提供了一個Excel表,它可以精確地將這個值限定在0.1%以內。
各種濾波器設計的蒙特卡羅分析
如果不對圖11和圖12中的各種濾波器設計進行蒙特卡洛分析,本文就不算完整。響應曲線以20dB的增量隔開,以便看得更清楚,而不會相互混淆。表1給出了圖11曲線的元件值。這再次證明,對于元件靈敏度低的濾波器,減法根不是一個好的選擇,同樣電容也不是。我們還看到使用Rr = Rf/Rg的最優值與較低和較高值進行比較的可取性。利用Rf相對于Rg的最優值,可以計算Rr。

圖11:各種濾波器設計的蒙特卡羅分析。
表1:圖11中曲線的元件值。
圖12:各種濾波器設計的蒙特卡洛分析,不同參數情況下的濾波器靈敏度存在差異,其中Q = 10,Ctol = 2.5,Cr = C2/C1比值分別為0.316、0.0316和0.00316。
圖12顯示了Q = 10,Ctol = 2.5,而Cr = C2/C1值分別為0.316、0.0316和0.00316時濾波器靈敏度的差異。這些已經用Rr的最優值計算出來了。表2列出了所有的濾波器元件值。
表2:所有的濾波器元件值。
一些猜測
我們只探討了Q = 10和Ctol = 2.5時的濾波器設計。這似乎是說,設計中R1和R2的值相當接近最佳Rr值。這個推論對于Q和Ctol的所有值都正確嗎?如果是這樣,即便我們使R1和R2相等并計算出結果Rr,靈敏度增加的可能也微乎其微。當然,閉合公式適用于所有元件。不過,有了Excel表,目前的方法會得到最佳的靈敏度,而且很容易使用。
設計Sallen Key低通濾波器從指定Q和ω0開始。Sallen Key濾波器諧振時使響應靈敏度最小化至元件值的黃金標準是選擇單位DC增益,其中Rf是短路和/或Rg是開路。這要求C1 = 4·Q2·C2。可以選擇C2的值并計算C1。然后,R1和R2可以由公式(2)和(3)確定,其中R2應該選擇加上而不是減去平方根。但對于高Q的情況,這可能并不總是一個理想的方法。在這些情況下,應在C1/C2具有可接受的最大比值時才選擇C2。設計中我們還需要知道電容容差與電阻容差的比值Ctol。應該為這些值找到最佳比Rr = Rf/Rg,使用前面提到的Excel表也許能找到。Excel表可以計算R1和R2,還可以選擇任意Rr值,為Rg和Rf,以及C1、C2、Q和ω0指定自己期望的值。然后,Excel表計算出R1和R2。
其它性能參數也可得到改善。使Rf||Rg = R1+R2,放大器偏置電流造成的失調將會最小。使C1||C2最大、Rf||Rg最小,元件阻抗和濾波噪聲將會降至最低。使C最小、Rf||Rg最大,功耗會降至最低。
-
電阻
+關注
關注
86文章
5528瀏覽量
172305 -
濾波器
+關注
關注
161文章
7846瀏覽量
178413
原文標題:設計對元件容差靈敏度最小的二階Sallen-Key低通濾波器
文章出處:【微信號:eet-china,微信公眾號:電子工程專輯】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
無源標簽芯片靈敏度測試設計介紹
無漂移有源低通濾波器的統計靈敏度優化
Butterworth濾波器設計的詳解
最大限度降低單運算放大器濾波器的元件變化靈敏度




 如何讓濾波器響應靈敏度在頻率ω0時達到最小
如何讓濾波器響應靈敏度在頻率ω0時達到最小










評論