什么是互易定理
在只含一個電壓源(或電流源),不含受控源的線性電阻電路中,電壓源(或電流源)與電流表(電壓表)互換位置,電流表(電壓表)讀數(shù)不變。這種性質(zhì)稱為互易定理。
在電磁學(xué)上,互易定理為洛侖茲互易定理(Lorentz Reciprocity Theorem),由卡森(J.R. Carson)導(dǎo)出而被稱為卡森形式的互易定理。互易定理即論述某些網(wǎng)絡(luò)具有的互易性質(zhì)的定理。互易性質(zhì)表現(xiàn)為:將網(wǎng)絡(luò)的輸入和特定輸出互換位置后,輸出不因這種換位而有所改變。具有互易性質(zhì)的網(wǎng)絡(luò)稱為互易網(wǎng)絡(luò)。互易性不僅一些電網(wǎng)絡(luò)有,某些聲學(xué)系統(tǒng)、力學(xué)系統(tǒng)等也有。互易定理是一個較有普遍意義的定理。
互易定理的性質(zhì)
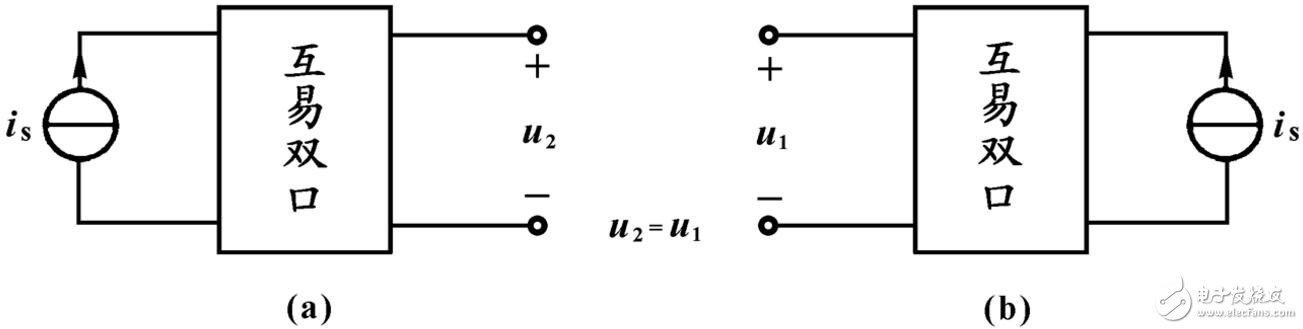
從圖中可以得出結(jié)論,圖(a)的電壓u2=R21/S與圖(b)的電壓u1=R12/S相同。也就是說,在互易網(wǎng)絡(luò)中電流源與電壓表互換位置,電壓表讀數(shù)不變。
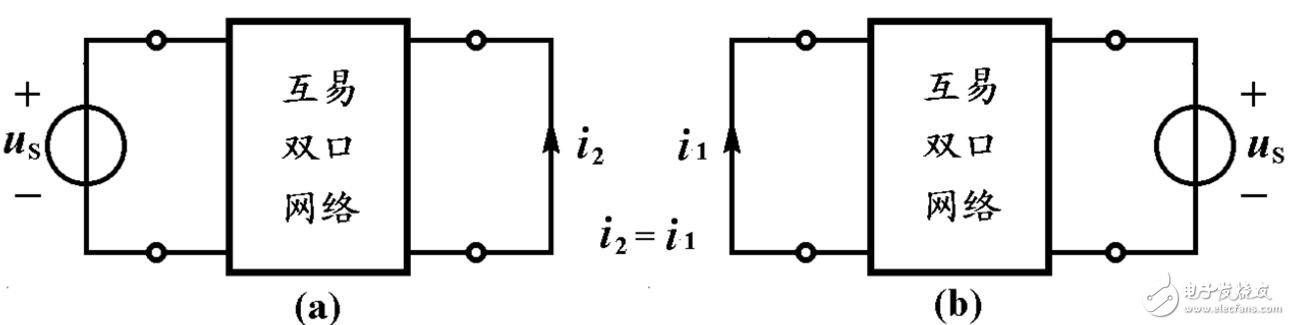
圖(a)的電流i2=G21uS與圖的電流i1=G12uS相同。也就是說互易網(wǎng)絡(luò)中電壓源與電流表互換位置,電流表讀數(shù)不變。
互易定理的幾種形式
1、互易定理的第一種形式
對于一個線性電阻電路,單一電壓源 U s 在 1-1’支路中作用,而在 2-2’支路中產(chǎn)生了電流 i 2 , i 2 的值等于將電壓源 U s 移到 2-2’支路上作用,在 1-1’支路中產(chǎn)生的電流 i1 的值。電流電壓方向選關(guān)聯(lián)參考方向。
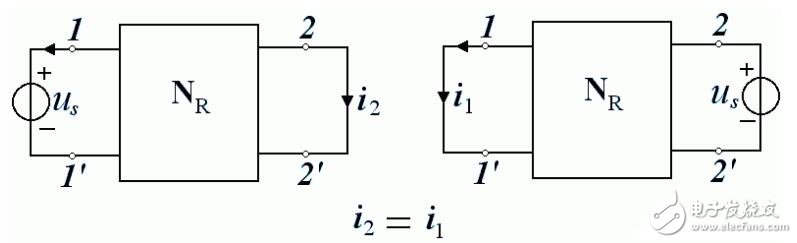
2、互易定理的第二種形式
對于一個線性電阻電路,單一電流源 i s 在 1-1’支路中作用,而在 2-2’支路中產(chǎn)生了電壓 u 2 , u 2 的值等于將電流源 i s 移到 2-2’支路上作用,在 1-1’支路中產(chǎn)生的電壓 u1 的值。電流電壓方向選關(guān)聯(lián)參考方向。
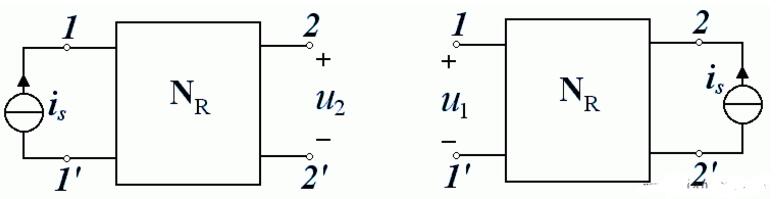
3、互易定理的第三種形式
對于一個線性電阻電路,單一電流源 i s 在 1-1’支路中作用,而在 2-2’支路中產(chǎn)生了電流 i 2 , i 2 的值等于將電流源 i s 移到 2-2’支路上作用,在 1-1’支路中產(chǎn)生的電流 i1 的值。電流電壓方向選關(guān)聯(lián)參考方向。
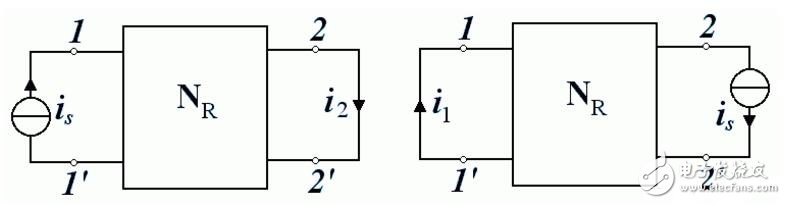
互易定理應(yīng)用條件
并非任何一個網(wǎng)絡(luò)都具有互易性質(zhì)。一般地說,由線性時不變的二端電阻元件、電感元件、電容元件、耦合電感器和理想變壓器連接而成的網(wǎng)絡(luò)均有此性質(zhì)。含有受控電源、非線性元件、時變元件、回轉(zhuǎn)器的網(wǎng)絡(luò)都不一定具有這種性質(zhì)。
互易定理的應(yīng)用
電路如圖所示,求電流i。
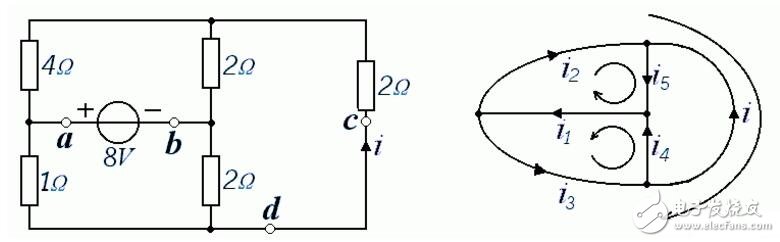
如果用支路電流法求解:b=6,n=4,要寫出b=6個方程:3個節(jié)KCL方程+3個回路KVL方程
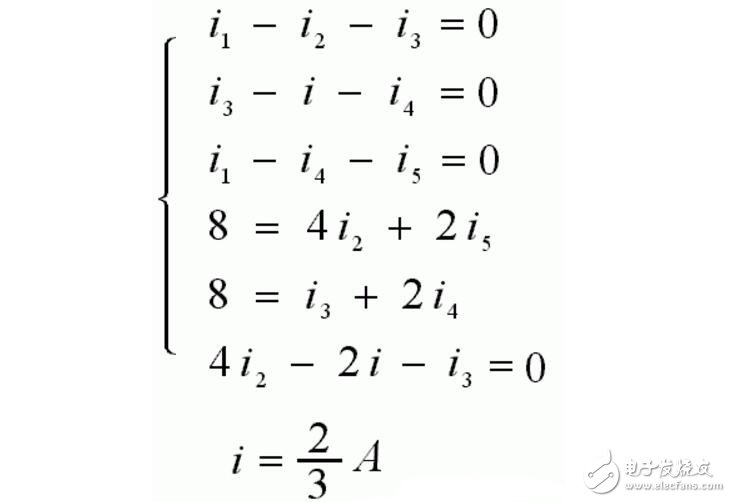
再用互易定理,原電路圖可改化如下:
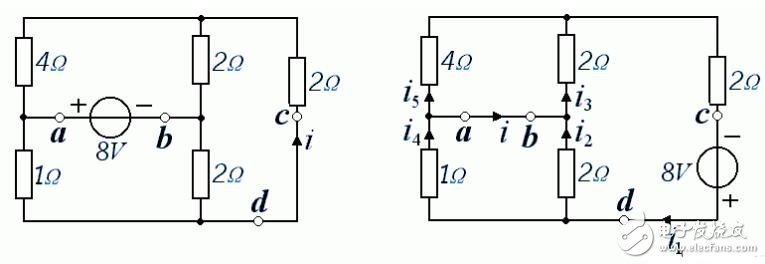
計算如下:
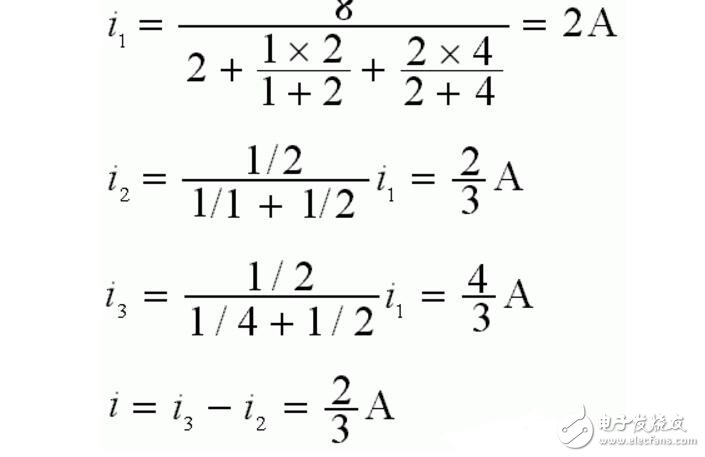
-
互易定理
+關(guān)注
關(guān)注
0文章
2瀏覽量
6344
發(fā)布評論請先 登錄
相關(guān)推薦




 電路的互易定理
電路的互易定理










評論