馬爾科夫鏈、主成分分析以及條件概率等概念，是計算機學生必學的知識點，然而理論的抽象性往往讓學生很難深入地去體會和理解。而本文，將這些抽象的理論概念，用可視化的方式來解釋，還可調節相應參數來改變結果，使這些抽象概念變得生動而立體！

計算機相關概念太難、太抽象？別怕，往下看！

人類對視覺信息的記憶要遠遠大于文字信息。使用圖表等形式的可視化，可以讓抽象、難懂的概念一目了然；在此基礎之上，添加可控的參數調節器，將更有助于對概念的深入學習與理解。

馬爾科夫鏈

馬爾科夫鏈是指數學中具有馬爾科夫性質的離散事件隨機過程。在其每一步中，系統根據概率分布可以從一個狀態變到另一個狀態，也可以保持當前狀態。狀態的改變叫做轉移，與不同的狀態改變相關的概率叫做轉移概率。

這概念是不是看著有點暈？沒關系，我們來看下面這張圖：

2種狀態的馬爾科夫鏈

在狀態空間中有兩種狀態，A和B。共有4種可能的轉換。如果我們在A，接下來可以過渡到B或留在A。如果我們在B，可以過渡到A或者留在B。在這張圖中，從任意狀態到任意狀態的轉移概率是0.5。

當然，真正的建模工作者不會總是就畫一張馬爾科夫鏈圖。 相反，他們會使用“轉移矩陣”來計算轉移概率。狀態空間中的每個狀態都會出現在表格中的一列或者一行中。矩陣中的每個單元格都告訴你從行狀態轉換到列狀態的概率。因此，在矩陣中，單元格做的工作和圖中的箭頭所示是一樣。

如果狀態空間添加了一個狀態，我們將添加一行和一列，向每個現有的列和行添加一個單元格。 這意味著當我們向馬爾可夫鏈添加狀態時，單元格的數量會呈二次方增長。因此，轉換矩陣就起到了很大的作用（除非你想把法爾科夫鏈圖畫的跟叢林一樣）。

馬爾科夫鏈的一個作用是用計算機模擬現實世界中的現象。例如，可以用來檢測一個新建的水壩溢流的頻率（取決于連續下雨的天數）。為建立這個模型，可以從下面的雨天（R）和晴天（S）開始：

表述這種模擬天氣的方法就是：“有一半的天數是下雨天。所以模擬中的每一天都有50%的概率是下雨的。”這個規則在模擬中所產生的序列如下：

你注意到上面的序列和原來的不太一樣了嗎?第二個序列似乎具有跳躍性，而第一個(真實數據)似乎具有“粘性”。在真實的數據中，如果某一天是晴天，那么第二天也很可能是晴天。

可以通過兩個狀態的馬爾可夫鏈來消除這種“粘性”。當馬爾科夫鏈處于狀態“R”時，它保持在該狀態的概率是0.9，狀態改變的概率是0.1。同樣，“S”狀態保持不變的概率是0.9，過渡到“R”狀態的概率是0.1。

在許多需要對大規模的現象做研究的工作人員手中，馬爾科夫鏈的作用可以變得非常強大。例如，谷歌用于確定搜索結果順序的算法，稱為PageRank，就是一種馬爾可夫鏈。

主成分分析（PCA）

主成分分析， 是一種統計方法。通過正交變換將一組可能存在相關性的變量轉換為一組線性不相關的變量，轉換后的這組變量叫主成分。PCA是最重要的降維方法之一,在數據壓縮消除冗余和數據噪音消除等領域都有廣泛的應用。

2D示例

首先，只考慮兩個維度的數據集，比如高度和重量。這個數據集可以繪制成平面上的點。但如果想要整理出變量，PCA會找到一個新的坐標系，其中每個點都有一個新的(x,y)值。坐標軸實際上沒有任何物理意義。它們是高度和重量的組合，被稱為“主分量”。

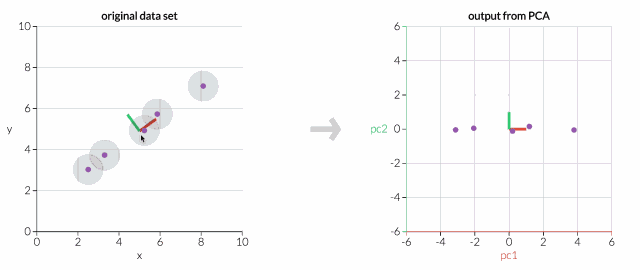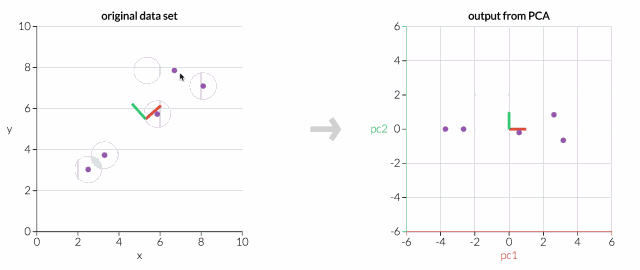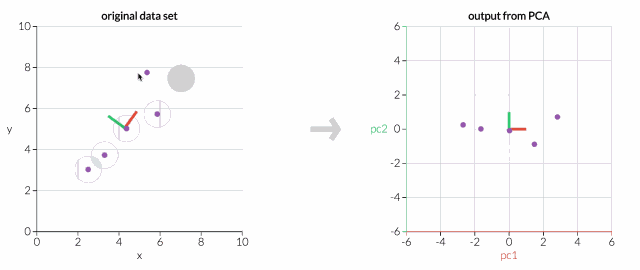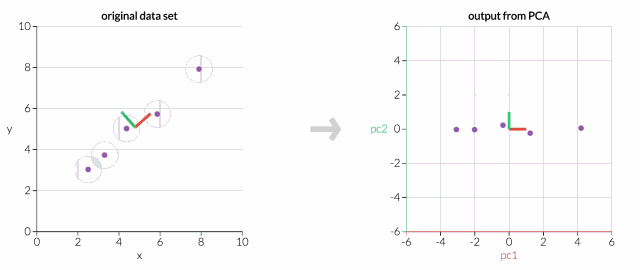
拖動原始數據集中的點，可以看到PC坐標系統正在調整

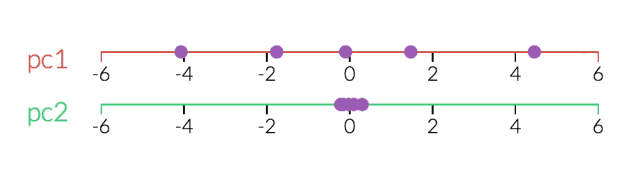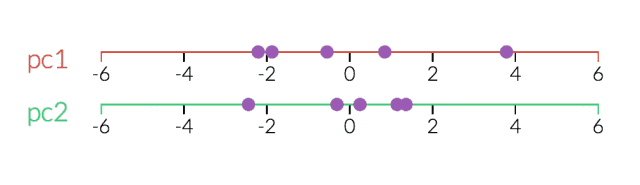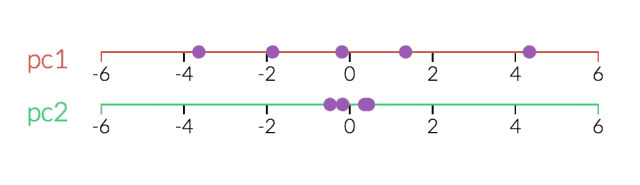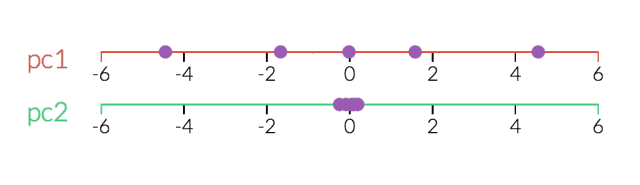
PCA對于降維很有用。下面，我們將數據繪制成兩條直線:一條由x值組成，另一條由y值組成。

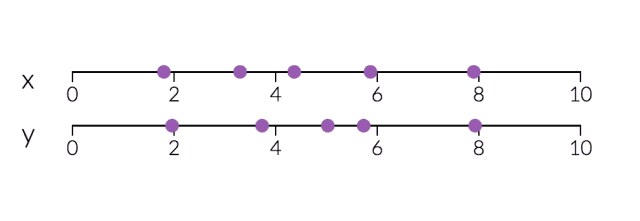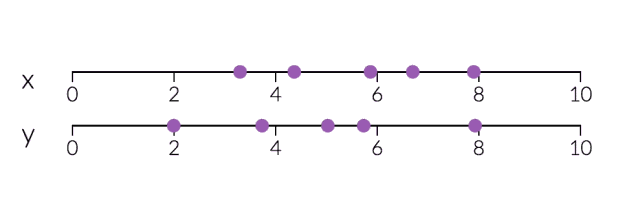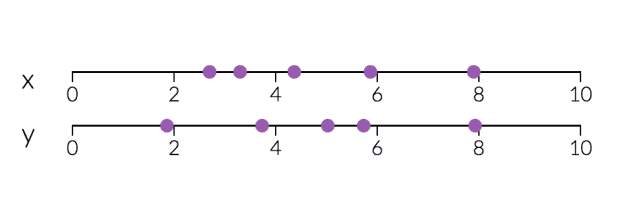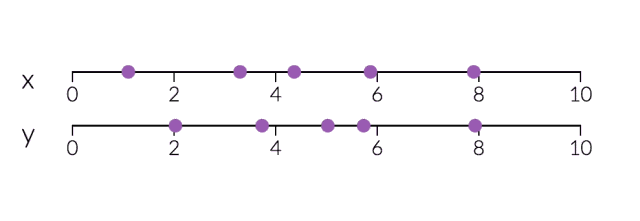
但是，如果我們只打算沿一個維度查看數據，那么將該維度作為具有最大變化的主成分可能會更好。 通過減少PC2，不會造成太大損失，因為它對數據集的變化貢獻最小。

3D示例

看透一個數據云是非常困難的，因此，在3D空間中，PCA顯得更為重要。在下面的示例中，原始數據以3D的形式繪制，但可以通過不同的視角，將其投射到2D空間。確定好角度之后，點擊“顯示PCA”按鈕，即可呈現2D的結果。在本例中，PCA變換確保水平軸PC1的變化量最大，垂直軸PC2的變化量次之，第三軸PC3的變化量最少。顯然，PC3是丟棄的。

應用：吃喝在英國

如果數據集不僅僅是三維的，而是17個維度的呢？！如下表所示：

表中是英國每個地區平均每人每周17種食物的消費量，單位為克。這張表顯示了不同食物類型之間存在的一些有趣的差異，但總體差異并不顯著。讓我們看看PCA是否可以通過降維來強地區家之間的差異。

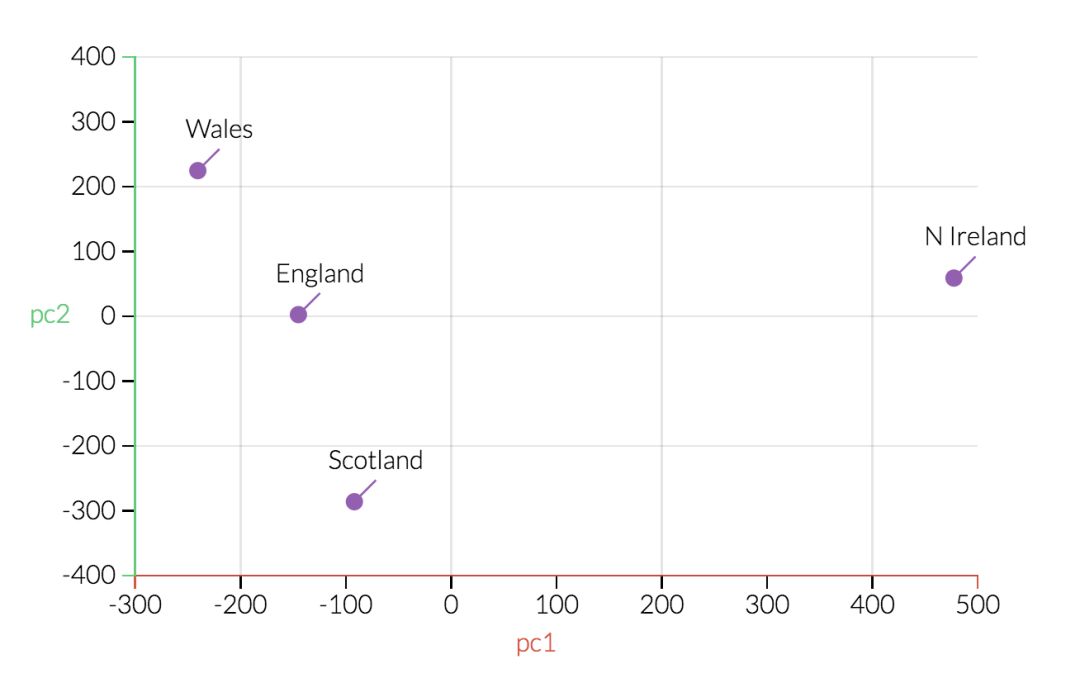
下圖是第一個主成分的數據圖。 我們可以看到一些有關北愛爾蘭的情況已經發生了變化。

現在，看看第一和第二主成分，可以看到北愛爾蘭是一個主要的異常值。一旦回過頭來看看表格中的數據，這就顯得很有道理了:北愛爾蘭人吃的新鮮土豆要很多，吃的新鮮水果、奶酪、魚和酒精飲料較少。這是一個很好的跡象，我們所看到的結構反映了現實世界地理的一個重要事實:北愛爾蘭是四個國家中唯一一個不在大不列顛島上的。

條件概率

條件概率是指一個事件在另外一個事件已經發生條件下的發生概率。一個落下來的球可能落在紅色的架子上(稱之為A事件)，或者落在藍色架子上(稱之為B事件)，或者兩者兼而有之。

那么給定一個球，它擊中了紅色架子（A事件），而后擊中藍色架子（B事件）的概率會是多少呢？可以通過給定A的條件概率，即P（B | A）來回答這個問題。

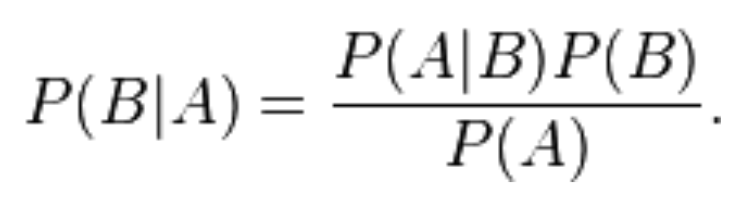
將抽象、難懂的計算機概念，以可視化的形式展現出來，可以幫助學生、研究者更好的理解；甚至可以幫助教師們提高教學質量。

無論如何，希望讀者們能從本文中得到或多或少的幫助。