如果你打算開一家咖啡館,你一定想知道:“附近最近的一家咖啡館在哪?”了解這些信息有助于應對商業競爭。
這種現象是計算機科學中廣泛研究的問題,稱為“最近鄰搜索”。它的問題是,給定數據集和新的數據點,數據集中哪個數據離新數據點最近?這個問題出現的場景非常豐富,可以是基因搜索、圖像查詢,或者音樂推薦。
但是最近鄰問題并不像咖啡館那么容易解決。過去幾十年,很多計算機科學家都在致力于尋找更好的解決辦法。與此同時,他們還要解決隨之而來的復雜情況,例如不同數據集對“相近”有著不同的定義。
現在,一個五人小組提出了開創性的解決辦法,他們在兩篇論文中(一篇已于4月發表,另一篇還未出爐)提出了解決復雜數據最近鄰問題的通用方法。
麻省理工學院的計算機科學家、最近鄰搜索領域的重要任務Piotr Indyk表示:“這是首個用單一算法捕捉大量空間的結果。”
不同的距離
我們已經習慣了用一種方法定義距離,常常會忽視其他方式。通常,我們用“歐幾里得距離”測量距離,即在兩點之間測量直線的距離。但在有些情況下,這樣的測量方式就說不通了。例如在街道網格中,就需要用到“曼哈頓距離”了,直線距離5英里的目的地,可能需要走3英里之后轉90°,再繼續走4英里才能到達。
另外,還可以用非地理的術語表示距離。比如Facebook上的兩名用戶、兩部電影、兩組基因之間的距離怎么計算?在這些問題上,“距離”表示的是兩個物體之間的相似程度。
有關距離的測量尺度有很多,例如兩組基因,生物學家會用“編輯距離(edit distance)”來比較二者。這樣一來,兩組基因序列之間的距離就是從一組基因轉換到另一組所需要添加、刪除、插入、替換的數字。
編輯距離和歐幾里得距離是兩種完全不同的距離測量方法,二者是不能相互替代的。但是這樣的情況對研究最近鄰算法的科學家們來說很棘手,能有效計算一種距離的算法在另一種情況下就無法工作了。
在夾縫中求生存
為了找到最近鄰,通常所用的方法是將數據分成好幾份。假設你的數據就像在牧場中吃草的奶牛,給分散在草場中的牛群畫不同的圓圈,現在進來了一頭新奶牛,問它會落在哪個圓圈里?可以肯定的是,這頭新奶牛的最近鄰一定也在這個圈里。
然后重復這一過程,不斷進行細分。最終會得到一個只包含兩頭牛的區域,這樣就找到了最近鄰。
現在,算法能夠完成這一過程,好的算法還會將這一任務完成得又快又好。這里“好”的標準可以理解成,算法不會得出最近鄰與新數據不在一個圈子里的結果。
近些年來,科學家們提出了多種分割數據的算法。對于低維數據(即每個數據點僅由少量的值定義,例如牧場中牛的位置),算法在解決最近鄰問題時會生成Voronoi圖。
對于高維數據(每個數據點可能有成百上千個值),Voronoi圖要計算起來就十分費力了。所以科學家們用“局部敏感哈希(LSH)算法”對數據進行分割,這種算法于1998年由Indyk和Rajeev Motwani共同提出。LSH算法是隨機對數據進行分類的,這使得它速度很快,但精確度較低。算法最終并不是找到確切的最近鄰點,而是告訴你最近鄰與已有數據的確切距離。(可以想象成在電影推薦時,推薦結果并不是最佳的,而是那些還不錯的。)
上世紀90年代末,計算機科學家們提出的LSH算法以特殊的距離尺度對最近鄰問題給出大致的解決方案。這些LSH算法都非常具體,無法通用。
“你可以為歐幾里得距離或曼哈頓距離設計非常高效的算法。但是我們沒有一種技術能在多種距離上通用,”Indyk說道。
受制于這種困境,科學家們想了一種應變方法:通過嵌入,在沒有好的算法的距離標準之上“覆蓋”一種距離尺度。但是這樣的結果往往不準確,有的時候嵌入根本無法完成。所以他們仍需要想出一種合適的通用方法。
驚人的結果
在這項新研究開始之際,科學家們回過頭思考當初具體的最近鄰算法追求的目標是什么。他們提出了一個更寬泛的問題:對距離尺度來說,阻礙一款好的最近鄰算法出現的原因是什么?
他們想原因可能與在尋找最近鄰時復雜的“擴展圖(expander graph)”有關。擴展圖是一群由線條連接起來的點。這些圖都有它們自己的距離尺度,圖中兩點之間的距離是你從一點到另一點所經過的最少線段。可以將其想象成社交網絡中的各種人脈關系。
擴展圖有兩個明顯矛盾的特點:它聯系廣泛,所以如果想切斷與某一點的聯系,就要切斷之間的線段。但同時,大多數點都和其他的點相連。所以,最終有些點會越來越遠。
這樣的特征造成的結果是,在擴展圖上可以很快地進行最近鄰搜索,而將數據點分割的過程可以看成將最近的兩點分開。
“任何分割擴展圖的方法都會切斷很多線,分開很多相近的點,”論文作者之一Waingarten說道。
從左至右:Alexandr Andoni、Ilya Razenshteyn、Erik Waingarten
2016年夏天,Andoni、Nikolov、Razenshteyn和Waingarten認為,是不可能存在對最近鄰算法有效的擴展圖的。但他們真正想證明的是,好的最近鄰算法同樣也不存在于其他距離尺度中。
他們證明的方法是在這些距離尺度中嵌入擴展尺度。這樣一來,他們可以確定這些尺度有類似擴展圖的無法工作的特征。
這四位科學家找到普林斯頓大學的Assaf Naor,他是一名數學家,同時也是計算機科學家,此前的研究非常適合回答有關擴展圖的問題。他們詢問了有關擴展圖嵌入到其他距離類型中的問題,但答案并非所期望的那樣,Assaf給出了完全相反的回答。
Naor證明,擴展圖并不能嵌入到多種距離尺度中,研究者將這一論斷作為基礎,接著這個邏輯鏈條開始思考:如果擴展圖不能嵌入到其他尺度,那么一個好的數據分割方法一定存在(因為他們證明擴展圖的特征是阻礙良好數據分割的障礙)。因此,良好最近鄰算法可能存在。
他們將發現結果寫在第一篇論文中,而第二篇論文本月也即將發表。Waingarten表示:“第一篇論文證明了確實存在一種方法能良好地進行數據分割,但沒有給出如何快速完成的方案。在第二篇論文中會詳細解釋。”
同時,這項新研究第一次用通用的方法對高維數據進行最近鄰搜索。“任何尺度空間都可以用該算法實現最近鄰搜索,”Waingarten說。
-
算法
+關注
關注
23文章
4622瀏覽量
93056 -
數據集
+關注
關注
4文章
1208瀏覽量
24737
原文標題:終于,「最近鄰搜索」有通用方法了
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Python實現k-近鄰算法
利用變體隊列實現任意復雜數據集合傳遞(很方便)
Python實現k-近鄰算法
改進的共享型最近鄰居聚類算法
改進GP分形理論的最近鄰序列預測算方法
Spark下的并行多標簽最近鄰算法
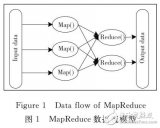
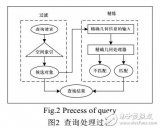
路網環境下的最近鄰查詢技術
最近鄰的隨機非線性降維
一種基于自然最近鄰的密度峰值聚類算法





 解決復雜數據最近鄰問題的通用方法
解決復雜數據最近鄰問題的通用方法












評論