全加器

全加器是一個能夠完成一位（二進制）數相加的部件。我們先來看一下兩個二進制數的加法運算是怎樣進行的。兩數相加，先從低開始，把對應位上的數相加，還可能有由較低位來的進位數。因此，除第一位外，每一位上參加運算的是三個數。所以，全加器應有三個輸入端，分別對應著被加數、加數和較低位來的進位數。相加的結果，得到本位的和數以及向較高位的進位數，因此，全加器有兩個輸出端，一個對應著本位和數，另一個對應著向較高位的進位數。于是，全加器的邏輯框圖如圖19-18所示。

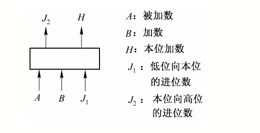
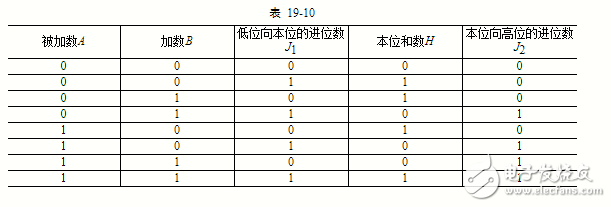
顯然，本位和數H、本位向較高位的進位數J2，都是被加數A、加數B和由較低位來的進位數J1的函數，列表如表19-10所示。由此可得H和J2的邏輯表達式的析取范式為：

H= (A'∧B'∧J1)∨(A'∧B∧J'1)∨(A∧B'∧J'1)∨(A∧B∧J1)

J2= (A'∧B∧J1)∨(A∧B'∧J1)∨(A∧B∧J'1)∨(A∧B∧J1)

化簡后得

H= (((A'∧B)∨(A∧B'))∧J'1)∨(((A'∨B)∧(A∨B')))∧J1)
= (H1∧J'1)∨(H'1∧J1)

其中

H1= (A'∧B)∨(A∧B')

而

J2= (A∧B)∨(H1∧J1)

為了用與門和非門電路構成全加器，將上式改寫為

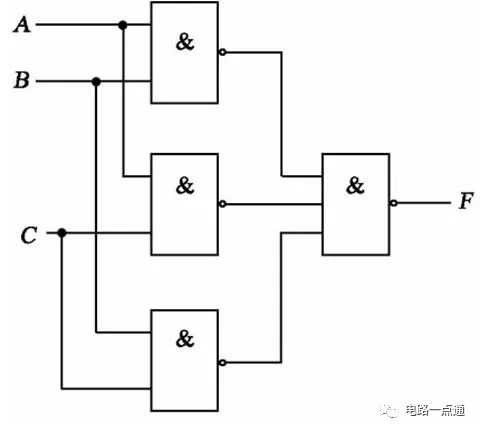
H1= ((A'∧B)'∧(A∧B')')'
H= ((H1∧J'1)'∧(H'1∧J1)')'
J2= ((A∧B)'∧(H1∧J1)')'

實現H1的開關電路如圖19-19a所示；實現H的開關電路如圖19-19b所示，它和圖19-19a具有相同的結構，只是輸入的變量不同；實現J2的開關電路如圖19-19c所示。

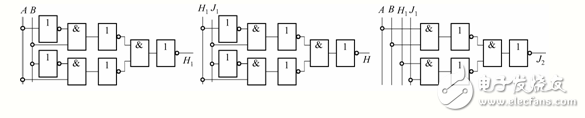
圖 19-19

把圖19-19a、b、c所示的電路連接在一起，就構成一個完整的一位全加器電路，如圖19-20所示。

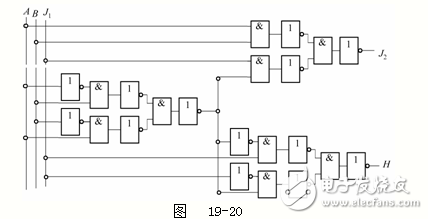
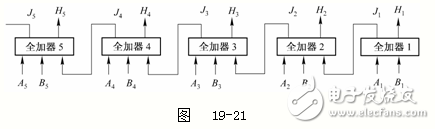
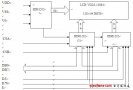
如果是兩個多位數相加，就要把多個全加器連接起來，構成加法器，圖19-21是五位加法器的框圖。