最優(yōu)化方法一直是機(jī)器學(xué)習(xí)中非常重要的部分,也是學(xué)習(xí)過程的核心算法。而 Adam 自 14 年提出以來就受到廣泛關(guān)注,目前該論文的引用量已經(jīng)達(dá)到了 10047。不過自去年以來,很多研究者發(fā)現(xiàn) Adam 優(yōu)化算法的收斂性得不到保證,ICLR 2017 的最佳論文也重點(diǎn)關(guān)注它的收斂性。在本文中,作者發(fā)現(xiàn)大多數(shù)深度學(xué)習(xí)庫的 Adam 實(shí)現(xiàn)都有一些問題,并在 fastai 庫中實(shí)現(xiàn)了一種新型 AdamW 算法。根據(jù)一些實(shí)驗(yàn),作者表示該算法是目前訓(xùn)練神經(jīng)網(wǎng)絡(luò)最快的方式。
Adam 過山車
Adam 優(yōu)化器之旅可以說是過山車(roller-coaster)式的。該優(yōu)化器于 2014 年推出,本質(zhì)上是一個(gè)出于直覺的簡單想法:既然我們明確地知道某些參數(shù)需要移動(dòng)得更快、更遠(yuǎn),那么為什么每個(gè)參數(shù)還要遵循相同的學(xué)習(xí)率?因?yàn)樽罱荻鹊钠椒礁嬖V我們每一個(gè)權(quán)重可以得到多少信號(hào),所以我們可以除以這個(gè),以確保即使是最遲鈍的權(quán)重也有機(jī)會(huì)發(fā)光。Adam 接受了這個(gè)想法,在過程中加入了標(biāo)準(zhǔn)方法,就這樣產(chǎn)生了 Adam 優(yōu)化器(稍加調(diào)整以避免早期批次出現(xiàn)偏差)!
首次發(fā)表之時(shí),深度學(xué)習(xí)社區(qū)都為來自原論文的一些圖表(如下圖)興奮不已:
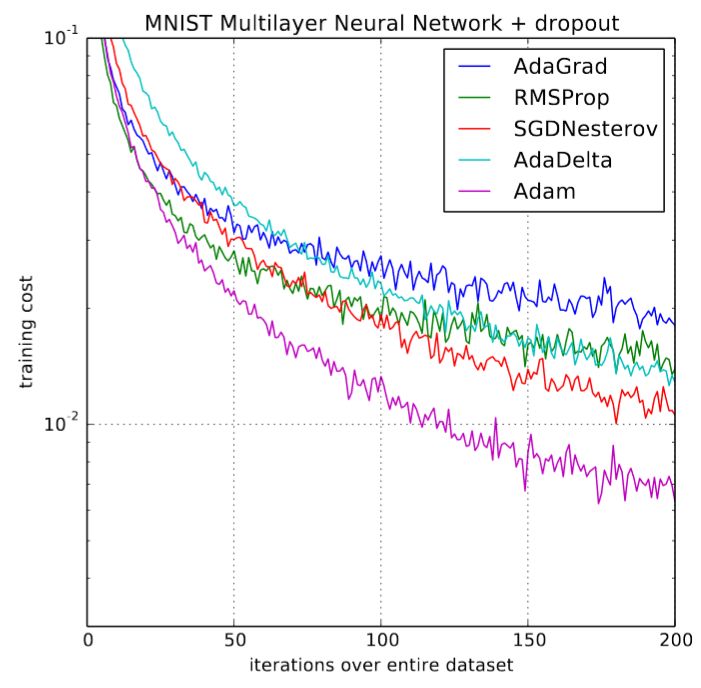
Adam 和其他優(yōu)化器的對(duì)比
訓(xùn)練速度提高 200%!「總體來看,我們發(fā)現(xiàn) Adam 非常魯棒,而且廣泛適用于機(jī)器學(xué)習(xí)領(lǐng)域的各種非凸優(yōu)化問題」論文結(jié)尾這樣寫道。那是三年前,深度學(xué)習(xí)的黃金時(shí)期。然而,事情并沒有按照我們期望的方向發(fā)展。使用 Adam 訓(xùn)練模型的研究文章少之又少,新的研究開始明顯地抑制了它的應(yīng)用,并在幾個(gè)實(shí)驗(yàn)中表明,SGD+momentum可能比復(fù)雜的 Adam 表現(xiàn)更好。2018 fast.ai 課程開課之際,可憐的 Adam 被從早期課程中刪除。
但是到了 2017 年末,Adam 似乎又重獲新生。Ilya Loshchilov 和 Frank Hutter 在他們的論文《Fixing Weight Decay Regularization in Adam》中指出,每個(gè)庫在 Adam 上實(shí)施的權(quán)重衰減似乎都是錯(cuò)誤的,并提出了一種簡單的方法(他們稱之為 AdamW)來修復(fù)它。盡管結(jié)果略有不同,但他們確實(shí)給出了一些類似下圖的令人鼓舞的圖表:
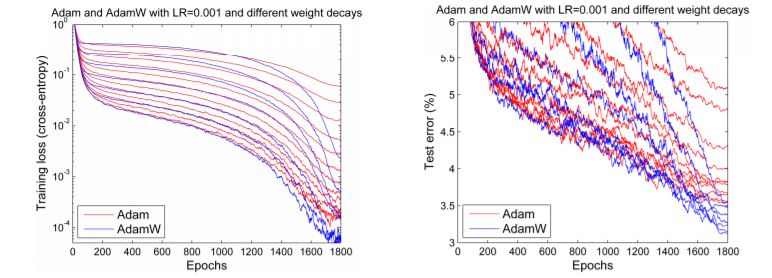
Adam 和 AdamW 對(duì)比
我們希望人們恢復(fù)對(duì) Adam 的熱情,因?yàn)樵搩?yōu)化器的一些早期結(jié)果似乎可以復(fù)現(xiàn)。但事與愿違。實(shí)際上,應(yīng)用它的唯一一個(gè)深度學(xué)習(xí)框架就是使用 Sylvain 編碼的 fastai。由于缺乏可用的廣泛框架,日常實(shí)踐者就只能固守又舊又不好用的 Adam。
但這不是唯一的問題。前面還有很多阻礙。兩篇論文指出了 Adam 在收斂性證明方面的明顯問題,盡管其中一篇提出了名為 AMSGrad 的修正(并在享有盛譽(yù)的 ICLR 大會(huì)上贏得了「最佳論文」獎(jiǎng))。但是,如果說我們從這種最戲劇化的生活(至少按照優(yōu)化器的標(biāo)準(zhǔn)來說是戲劇化的)簡史中學(xué)到了什么,那就是,沒有什么是它表面看起來的樣子。的確,博士生 Jeremy Bernstein 指出,所謂的收斂問題其實(shí)只是選擇不當(dāng)?shù)某瑓?shù)的跡象,也許 AMSGrad 也解決不了問題。另一名博士生 Filip Korzeniowski 展示了一些早期成果,似乎支持了 AMSGrad 這種令人沮喪的觀點(diǎn)。
啟動(dòng)過山車
那么我們這些只希望快速訓(xùn)練精確模型的人該做些什么呢?我們選擇用數(shù)百年來解決科學(xué)辯論的方式——科學(xué)實(shí)驗(yàn)——來解決這一爭議!稍后將呈現(xiàn)所有細(xì)節(jié),但首先讓我們來看一下大致結(jié)果:
適當(dāng)調(diào)參之后,Adam 真的可以用!我們?cè)谝韵聨讉€(gè)任務(wù)中得到了訓(xùn)練時(shí)間方面的最新結(jié)果:
在含有測試時(shí)間增加的僅僅 18 個(gè) epoch 或 30 個(gè) epoch 上訓(xùn)練 CIFAR10,直到其準(zhǔn)確率超過 94%,如 DAWNBench 競賽;
對(duì) Resnet50 進(jìn)行調(diào)參,直至其在斯坦福汽車數(shù)據(jù)集上的準(zhǔn)確率達(dá)到 90%,只需訓(xùn)練 60 個(gè) epoch(之前達(dá)到相同的準(zhǔn)確率需要 600 個(gè) epoch);
從零開始訓(xùn)練一個(gè) AWD LSTM or QRNN,歷經(jīng) 90 個(gè) epoch(或在一個(gè) GPU 上訓(xùn)練 1 個(gè)半小時(shí)),其困惑度在 Wikitext-2 上達(dá)到當(dāng)前最優(yōu)水平(之前的 LSTM 需要 750 個(gè) epoch,QRNN 需要 500 個(gè) epoch)。
這意味著我們已經(jīng)看到使用 Adam 的超收斂!超收斂是訓(xùn)練學(xué)習(xí)率高的神經(jīng)網(wǎng)絡(luò)時(shí)出現(xiàn)的一種現(xiàn)象,它表示節(jié)省了一半訓(xùn)練過程。在 AdamW 之前,訓(xùn)練 CIFAR10 至 94 % 的準(zhǔn)確率需要大約 100 個(gè) epoch。
與之前的工作相比,我們發(fā)現(xiàn)只要調(diào)整得當(dāng),Adam 在我們嘗試過的每一個(gè) CNN 圖像問題上都可以獲得與 SGD+Momentum 一樣好的準(zhǔn)確率,而且?guī)缀蹩偸强煲稽c(diǎn)。
關(guān)于 AMSGrad 是一個(gè)糟糕的「解決方案」的建議是正確的。我們一直發(fā)現(xiàn),AMSGrad 在準(zhǔn)確率(或其他相關(guān)指標(biāo))上沒有獲得比普通 Adam / AdamW 更高的增益。
當(dāng)你聽到人們說 Adam 的泛化性能不如 SGD+Momentum 時(shí),你基本上總會(huì)發(fā)現(xiàn)他們?yōu)樽约旱哪P退x擇的超參數(shù)不咋地。通常 Adam 需要的正則化比 SGD 多,因此在從 SGD 轉(zhuǎn)向 Adam 時(shí),確保調(diào)整正則化超參數(shù)。
文章結(jié)構(gòu):
1. AdamW
理解 AdamW
實(shí)現(xiàn) AdamW
AdamW 實(shí)驗(yàn)和 AdamW-ish
2. AMSGrad
理解 AMSGrad
實(shí)現(xiàn) AMSGrad
AMSGrad 實(shí)驗(yàn)的結(jié)果
3. 完整結(jié)果圖表
AdamW
理解 AdanW:權(quán)重衰減與 L2 正則化
L2 正則化是減少過擬合的經(jīng)典方法,它會(huì)向損失函數(shù)添加由模型所有權(quán)重的平方和組成的懲罰項(xiàng),并乘上特定的超參數(shù)以控制懲罰力度。以下本文所有的方程式都是用 Python、NumPy 和 PyTorch 風(fēng)格的表達(dá)方式:
final_loss=loss+wd*all_weights.pow(2).sum()/2
其中 wd 為我們?cè)O(shè)置的超參數(shù),用以控制懲罰力度。這也可以稱為權(quán)重衰減,因?yàn)槊恳淮芜\(yùn)用原版 SGD 時(shí),它都等價(jià)于使用如下方程式更新權(quán)重:
w=w-lr*w.grad-lr*wd*w
其中 lr 表示學(xué)習(xí)率、w.grad 表示損失函數(shù)對(duì) w 的導(dǎo)數(shù),而后面的 wd * w 則表示懲罰項(xiàng)對(duì) w 的求導(dǎo)結(jié)果。在這個(gè)等式中,我們會(huì)看到每一次更新都會(huì)減去一小部分權(quán)重,這也就是「衰減」的來源。
fast.ai 查看過的所有庫都使用第一種形式。在實(shí)踐中,幾乎都是通過向梯度 wd*w 而實(shí)現(xiàn)算法,而不是真正地改變損失函數(shù)。因?yàn)槲覀儾⒉幌M黾宇~外的計(jì)算量來修正損失,尤其是還有其它簡單方法的時(shí)候。
既然它們是同一種表達(dá),那么我們?yōu)槭裁葱枰獏^(qū)分這兩種概念呢?原因在于它們只對(duì)于原版 SGD 是等價(jià)的,而當(dāng)我們添加動(dòng)量或使用如 Adam 那樣復(fù)雜的最優(yōu)化方法,L2 正則化(第一個(gè)方程)和權(quán)重衰減(第二個(gè)方程)就會(huì)存在很大的不同。在本文其余的部分中,我們討論權(quán)重衰減指的都是第二個(gè)方程式,而討論 L2 正則化都是討論第一個(gè)經(jīng)典方式。
如下在帶動(dòng)量的 SGD 中,L2 正則化與權(quán)重衰減是不等價(jià)的。L2 正則化會(huì)將 wd*w 添加到梯度中,但現(xiàn)在權(quán)重并不是直接減去梯度。首先我們需要計(jì)算移動(dòng)均值:
moving_avg=alpha*moving_avg+(1-alpha)*(w.grad+wd*w)
然后權(quán)重才能通過減去乘上了學(xué)習(xí)率的移動(dòng)均值而得到更新。所以 w 更新中涉及到的正則化為 lr* (1-alpha)*wd * w 加上已經(jīng)在 moving_avg 中前面權(quán)重的組合。
因此,權(quán)重衰減的更新方式可以表示為:
moving_avg=alpha*moving_avg+(1-alpha)*w.gradw=w-lr*moving_avg-lr*wd*w
我們可以觀察到,從 w 中減去有關(guān)正則化的部分在兩種方法中是不同的。當(dāng)我們使用 Adam 優(yōu)化器時(shí),權(quán)重衰減的部分可能相差更大。因?yàn)?Adam 中的 L2 正則化需要添加 wd*w 到梯度中,并分別計(jì)算梯度及其平方的移動(dòng)均值,然后再能更新權(quán)重。然而權(quán)重衰減方法只是簡單地更新權(quán)重,并每次從權(quán)重中減去一點(diǎn)。
顯然這是兩種不同的方法,在進(jìn)行了實(shí)驗(yàn)后,Ilya Loshchilov 和 Frank Hutter 建議我們應(yīng)該在 Adam 算法中使用權(quán)重衰減方法,而不是像經(jīng)典深度學(xué)習(xí)庫中實(shí)現(xiàn)的 L2 正則化。
實(shí)現(xiàn) AdamW
那么我們要如何才能實(shí)現(xiàn) AdamW 算法呢?如果你們?cè)谑褂?fastai 的庫,那么在使用 fit 函數(shù)時(shí)添加參數(shù) use_wd_sched=True 就能簡單地實(shí)現(xiàn):
learn.fit(lr,1,wds=1e-4,use_wd_sched=True)
如果你更喜歡新的訓(xùn)練 API,你就能在每一個(gè)訓(xùn)練階段中使用參數(shù) wd_loss=False:
phases=[TrainingPhase(1,optim.Adam,lr,wds=1-e4,wd_loss=False)]learn.fit_opt_sched(phases)
以下簡要地概述了 fastai 是如何實(shí)現(xiàn) AdamW 的。在優(yōu)化器中的階梯函數(shù),我們只需要使用梯度修正參數(shù),根本不使用參數(shù)本身的值(除了權(quán)重衰減,我們將在外部處理它)。然后我們可以在最優(yōu)化器之前通簡單的實(shí)現(xiàn)權(quán)重衰減,但這仍需要在計(jì)算梯度后才能完成,否則它就會(huì)影響梯度的值。所以在訓(xùn)練循環(huán)中,我們必須確定計(jì)算權(quán)重衰減的位置。
loss.backward()#Dotheweightdecayhere!optimizer.step()
當(dāng)然,最優(yōu)化器應(yīng)該設(shè)定 wd=0,否則它還會(huì)做一些 L2 正則化,這也是我們不希望看到的。現(xiàn)在在權(quán)重衰減的位置中,我們可以在所有參數(shù)上寫一個(gè)循環(huán)語句,并依次采用權(quán)重衰減的更新。而我們的參數(shù)應(yīng)該存儲(chǔ)在優(yōu)化器的字典 param_groups 中,所以這個(gè)循環(huán)應(yīng)該表示為如下語句:
loss.backward()forgroupinoptimizer.param_groups():forparamingroup['params']:param.data=param.data.add(-wd*group['lr'],param.data)optimizer.step()
AdamW 實(shí)驗(yàn)的結(jié)果:它真的能行嗎?
我們首先在計(jì)算機(jī)視覺問題上進(jìn)行測試,效果非常好。具體來說,Adam 和 L2 正則化在 30 個(gè) epoch 中獲得的平均準(zhǔn)確率為 93.96%,在兩次中有一次超過 94%。我們選擇 30 個(gè) epoch 是因?yàn)橥ㄟ^ 1cycle 策略和 SGD 可以獲得 94% 準(zhǔn)確率。當(dāng)我們使用 Adam 與權(quán)重衰減方法,我們持續(xù)獲得 94% 到 94.25% 的準(zhǔn)確率。為此,我們發(fā)現(xiàn)使用 1cycle 策略時(shí)的最優(yōu) beta2 值為 0.99。我們將 beta1 參數(shù)視為 SGD 中的動(dòng)量,這也就意味著它學(xué)習(xí)率的增長由 0.95 降低到 0.85,然后隨學(xué)習(xí)率的降低而又增加到 0.95。
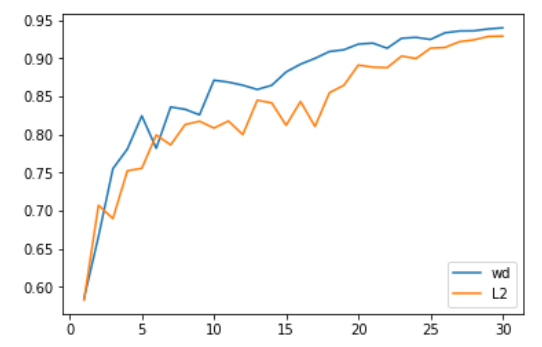
L2 正則化或權(quán)重衰減準(zhǔn)確率
更令人印象深刻的是,使用測試時(shí)間增加(即在測試集的一個(gè)圖像和它四個(gè)增加數(shù)據(jù)的版本上取預(yù)測的平均值),我們可以在僅僅 18 個(gè) epoch 內(nèi)達(dá)到 94 % 的準(zhǔn)確率(平均 93.98 %)!通過簡單的 Adam 和 L2 正則化,每嘗試 20 次就會(huì)出現(xiàn)一次超過 94 % 的情況。
在這些比較中需要考慮的一點(diǎn)是,改變正則化方式會(huì)改變權(quán)重衰減或?qū)W習(xí)率的最佳值。在我們進(jìn)行的測試中,L2 正則化的最佳學(xué)習(xí)率為 1e-6(最大學(xué)習(xí)率為 1e-3),而權(quán)重衰減的最佳值為 0.3(學(xué)習(xí)率為 3e-3)。在我們的所有測試中,數(shù)量級(jí)的差異都是非常一致的,主要是因?yàn)?L2 正則化被梯度的平均范數(shù)(相當(dāng)?shù)停┯行У貏澐郑⑶?Adam 的學(xué)習(xí)率相當(dāng)小(所以權(quán)重衰減的更新需要更強(qiáng)的系數(shù))。
那么,權(quán)重衰減總是比 Adam 的 L2 正則化更好?我們還沒有發(fā)現(xiàn)明顯更糟的情況,但無論是遷移學(xué)習(xí)問題(例如斯坦福汽車數(shù)據(jù)集上 Resnet50 的微調(diào))還是 RNNs,它都沒有給出更好的結(jié)果。
AMSGrad
理解 AMSGrad
AMSGrad 是由 Sashank J. Reddi、Satyen Kale 和 Sanjiv Kumar 在近期的一篇文章中介紹的。通過分析 Adam 優(yōu)化器收斂的證明,他們?cè)诟乱?guī)則中發(fā)現(xiàn)了一個(gè)錯(cuò)誤,該錯(cuò)誤可能導(dǎo)致算法收斂到次優(yōu)點(diǎn)。他們?cè)O(shè)計(jì)了理論實(shí)驗(yàn),展示 Adam 失敗的情形,并提出了一個(gè)簡單的解決方案。機(jī)器之心也曾從適應(yīng)性學(xué)習(xí)率算法出發(fā)分析過這一篇最佳論文:Beyond Adam。
為了更好地理解錯(cuò)誤和解決方案,讓我們來看一下 Adam 的更新規(guī)則:
avg_grads=beta1*avg_grads+(1-beta1)*w.gradavg_squared=beta2*(avg_squared)+(1-beta2)*(w.grad**2)w=w-lr*avg_grads/sqrt(avg_squared)
我們剛剛跳過了偏差校正(對(duì)訓(xùn)練的開始很有用),把重心放在了主要點(diǎn)上。作者發(fā)現(xiàn) Adam 收斂證明中的錯(cuò)誤之處在于:
lr/sqrt(avg_squared)
這是我們朝著平均梯度方向邁出的一步,在訓(xùn)練中逐漸減少。由于學(xué)習(xí)率常常是恒定或遞減的,作者提出的解決方案是通過添加另一個(gè)變量來跟蹤它們的最大值,從而迫使 avg _ square 量增加。
實(shí)現(xiàn) AMSGrad
相關(guān)文章在 ICLR 2018 中獲得了一項(xiàng)大獎(jiǎng)并廣受歡迎,而且它已經(jīng)在兩個(gè)主要的深度學(xué)習(xí)庫——PyTorch 和 Keras 中實(shí)現(xiàn)。所以,我們只需傳入?yún)?shù) amsgrad = True 即可。
avg_grads=beta1*avg_grads+(1-beta1)*w.gradavg_squared=beta2*(avg_squared)+(1-beta2)*(w.grad**2)max_squared=max(avg_squared,max_squared)w=w-lr*avg_grads/sqrt(max_squared)
AMSGrad 實(shí)驗(yàn)結(jié)果:大量噪音都是沒用的
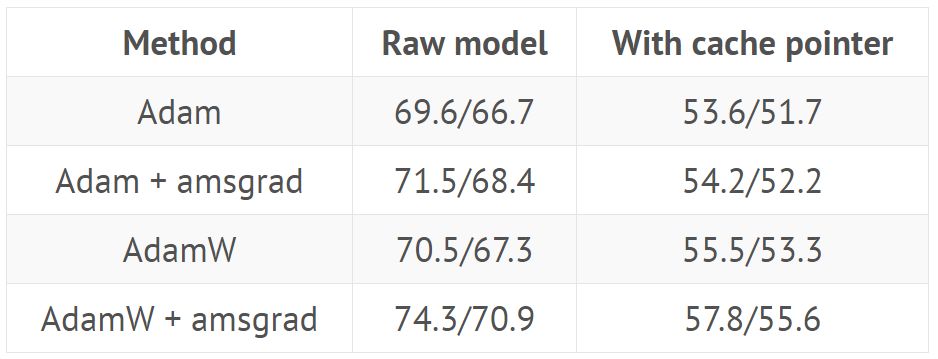
AMSGrad 的結(jié)果令人非常失望。在所有實(shí)驗(yàn)中,我們都發(fā)現(xiàn)它沒有絲毫幫助。即使 AMSGrad 發(fā)現(xiàn)的最小值有時(shí)比 Adam 達(dá)到的最小值稍低(在損失方面),其度量(準(zhǔn)確率、f_1 分?jǐn)?shù)…)最終總是更糟(詳見引言中的表格)。
Adam 優(yōu)化器在深度學(xué)習(xí)中收斂的證明(因?yàn)樗槍?duì)凸問題)和他們?cè)谄渲邪l(fā)現(xiàn)的錯(cuò)誤對(duì)于與現(xiàn)實(shí)問題無關(guān)的合成實(shí)驗(yàn)很重要。實(shí)際測試表明,當(dāng)這些 avg _ square 梯度想要減小時(shí),這么做能得到最好的結(jié)果。
這表明,即使把重點(diǎn)放在理論上有助于獲得一些新想法,也沒有什么可以取代實(shí)驗(yàn)(而且很多實(shí)驗(yàn)!)以確保這些想法實(shí)際上有助于從業(yè)人員訓(xùn)練更好的模型。
附錄:所有結(jié)果
從零開始訓(xùn)練 CIFAR10(模型是 Wide-ResNet-22,以下為五個(gè)模型的平均結(jié)果):

使用 fastai 庫引入的標(biāo)準(zhǔn)頭對(duì)斯坦福汽車數(shù)據(jù)集上的 Resnet 50 進(jìn)行微調(diào)(解凍前對(duì)頭訓(xùn)練 20 個(gè) epoch,并用不同的學(xué)習(xí)率訓(xùn)練 40 個(gè) epoch):

使用來自 GitHub(https://github.com/salesforce/awd-lstm-lm)的超參數(shù)訓(xùn)練 AWD LSTM(結(jié)果顯示在有或沒有緩存指針(cache pointer)情況下驗(yàn)證/測試集的困惑度):
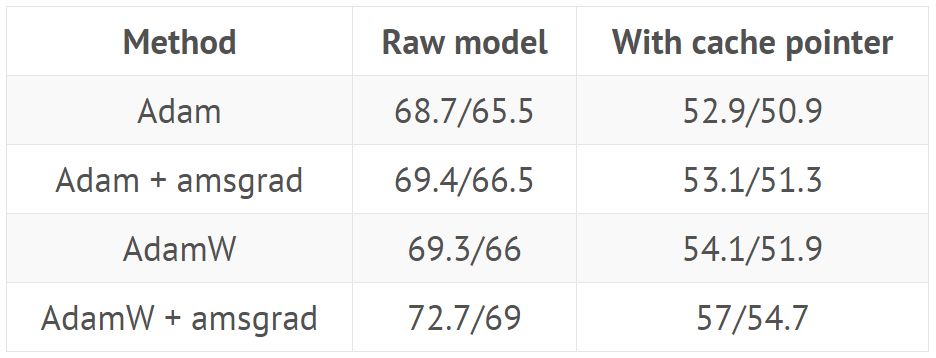
使用來自 GitHub repo 的超參數(shù)訓(xùn)練 QRNN(結(jié)果顯示在有或沒有緩存指針情況下驗(yàn)證/測試集的困惑度):
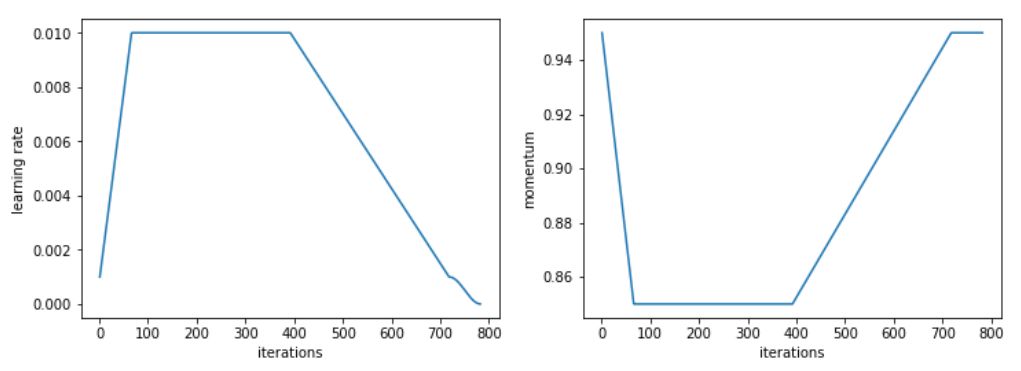
針對(duì)這一具體任務(wù),我們采用了 1cycle 策略的修改版本,加快了學(xué)習(xí)速度,之后長時(shí)間保持較高的恒定學(xué)習(xí)速度,然后再往下降。
Adam 和其它優(yōu)化器之間的對(duì)比
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4775瀏覽量
100921 -
算法
+關(guān)注
關(guān)注
23文章
4622瀏覽量
93086 -
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8428瀏覽量
132820
原文標(biāo)題:當(dāng)前訓(xùn)練神經(jīng)網(wǎng)絡(luò)最快的方式:AdamW優(yōu)化算法+超級(jí)收斂
文章出處:【微信號(hào):CAAI-1981,微信公眾號(hào):中國人工智能學(xué)會(huì)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
人工神經(jīng)網(wǎng)絡(luò)原理及下載
粒子群優(yōu)化模糊神經(jīng)網(wǎng)絡(luò)在語音識(shí)別中的應(yīng)用
【案例分享】ART神經(jīng)網(wǎng)絡(luò)與SOM神經(jīng)網(wǎng)絡(luò)
分享一種400×25×2的三層BP神經(jīng)網(wǎng)絡(luò)
隱藏技術(shù): 一種基于前沿神經(jīng)網(wǎng)絡(luò)理論的新型人工智能處理器
一種基于高效采樣算法的時(shí)序圖神經(jīng)網(wǎng)絡(luò)系統(tǒng)介紹
如何進(jìn)行高效的時(shí)序圖神經(jīng)網(wǎng)絡(luò)的訓(xùn)練
一種BP神經(jīng)網(wǎng)絡(luò)改進(jìn)算法的研究及應(yīng)用
基于動(dòng)態(tài)神經(jīng)網(wǎng)絡(luò)的交通事件檢測算法




 目前訓(xùn)練神經(jīng)網(wǎng)絡(luò)最快的方式一種新型AdamW算法
目前訓(xùn)練神經(jīng)網(wǎng)絡(luò)最快的方式一種新型AdamW算法










評(píng)論