基本上所有的結(jié)構(gòu)工程師都會(huì)使用到圣維南原理。大多數(shù)結(jié)構(gòu)力學(xué)教科書都收錄了基于該原理的各種公式，但至今尚未對(duì)其進(jìn)行嚴(yán)格證明。圣維南原理指出，只要載荷的合力正確，那么在遠(yuǎn)離載荷作用區(qū)的地方，載荷的精確分布就不重要。在本文中，我們將采用有限元分析對(duì)圣維南原理進(jìn)行探究。

圣維南原理的歷史

1855 年，法國科學(xué)家圣維南（Barré de Saint-Venant）發(fā)表了一個(gè)著名原理，但與其說這是一個(gè)嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)命題，不如說是一個(gè)觀察發(fā)現(xiàn)：

“如果作用在彈性體一小塊表面上的力被作用于同一塊表面上的靜力等效力系替代，這種替換僅使局部表面產(chǎn)生顯著的應(yīng)力變化，而在比應(yīng)力變化表面的線性尺寸更遠(yuǎn)的地方，其影響可忽略不計(jì)。”

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

圣維南肖像。圖像來源于公有領(lǐng)域，通過 Wikimedia Commons 共享。

在應(yīng)用力學(xué)領(lǐng)域，Boussinesq、Love、von Mises、Toupin 等科學(xué)家都對(duì)這一原理進(jìn)行了精準(zhǔn)的敘述，并給出了數(shù)學(xué)證明。但是對(duì)于很多一般性問題，論證圣維南原理具有很大難度，所以對(duì)該課題的研究仍在繼續(xù)（有些論據(jù)相當(dāng)鮮明）。

簡(jiǎn)單案例：遠(yuǎn)距離應(yīng)力分析

讓我們從一個(gè)簡(jiǎn)單的案例開始：對(duì)矩形薄板施加軸向拉力，與載荷作用邊相隔一段距離處有一個(gè)圓孔。假如我們要分析孔的應(yīng)力集中，那么實(shí)際的載荷分布有多重要呢？

我們對(duì)右側(cè)邊界施加了三種不同類型的載荷：

100 MPa 的恒定軸向應(yīng)力

峰值振幅為 150 MPa 的對(duì)稱拋物線應(yīng)力分布

等于上述兩種載荷工況合力的中心點(diǎn)載荷

如下方繪圖所示，載荷施加方式不影響孔周圍的應(yīng)力分布。當(dāng)然，關(guān)鍵在于孔距離載荷足夠遠(yuǎn)。

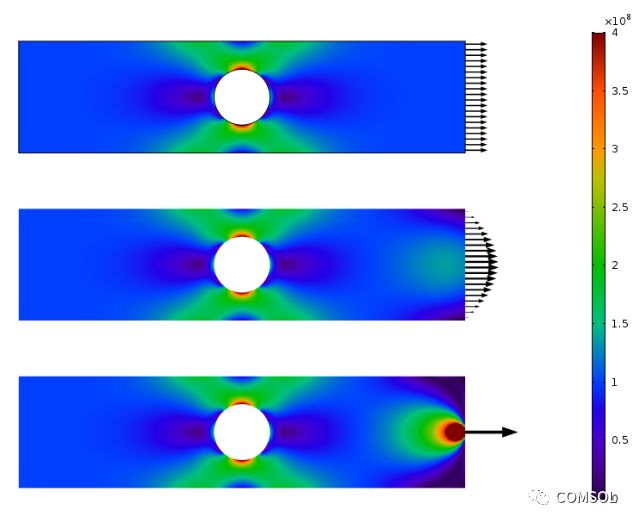
三種載荷工況對(duì)應(yīng)的 Von Mises 應(yīng)力分布。

該場(chǎng)景也可以使用箭頭圖來繪制主應(yīng)力。此圖將應(yīng)力場(chǎng)繪制為通量，從而清晰地展示了應(yīng)力重新分布的變化。

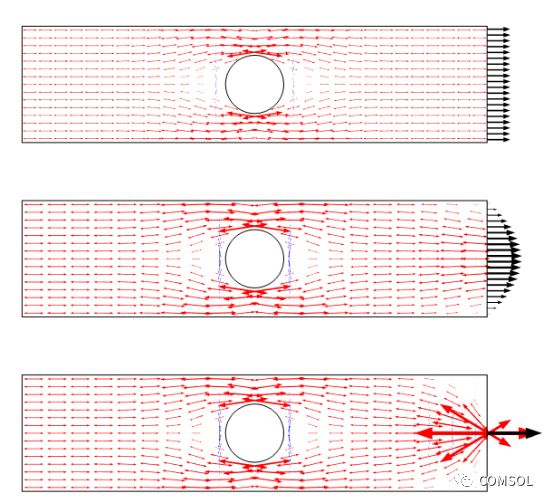
三種載荷工況的主應(yīng)力繪圖。請(qǐng)注意，使用點(diǎn)載荷時(shí)出現(xiàn)了一個(gè)奇異點(diǎn)。

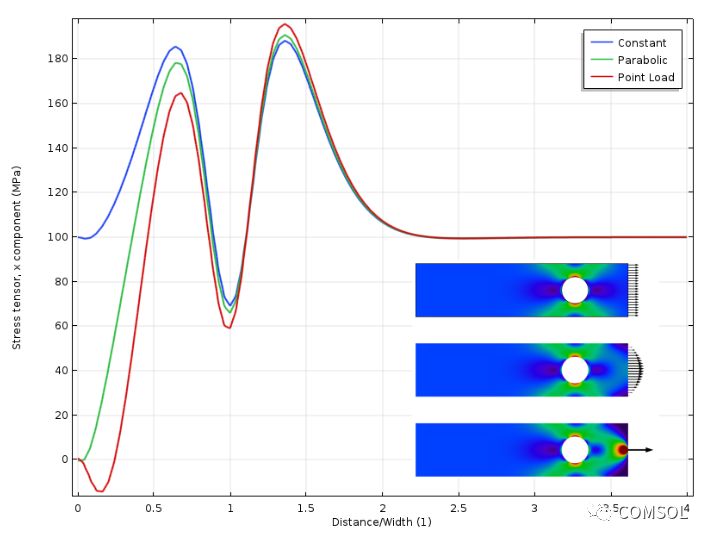
通過繪制應(yīng)力曲線，我們發(fā)現(xiàn)當(dāng)圓孔與受力邊相距一定距離后，三種工況的曲線就會(huì)聚在一起，這個(gè)距離大約等于板的寬度。

頂邊上的應(yīng)力隨與受力邊界間距的變化而變化。距離為通過板寬進(jìn)行標(biāo)準(zhǔn)化后的值。

如果孔向載荷作用邊靠近，結(jié)果就會(huì)不同。這時(shí)，孔周圍的應(yīng)力狀況取決于應(yīng)力分布。更有意思的是，孔到三個(gè)應(yīng)力場(chǎng)趨向一致的位置的距離是到載荷邊界距離的兩倍。應(yīng)用圣維南原理的前提是應(yīng)力可以自由地重新分布。然而在此例中，孔在一定程度上阻礙了應(yīng)力重新分布。

孔離受力邊更近時(shí)，頂邊的應(yīng)力分布。

值得注意的是，圣維南原理指出：當(dāng)距離大約等于載荷作用區(qū)的線性尺寸量級(jí)時(shí)，應(yīng)力狀態(tài)沒有差別。不過，要考慮的受載區(qū)卻未必是真正加載的地方！這個(gè)說法聽起來或許很奇怪，我們可以這樣想：當(dāng)孔距離較遠(yuǎn)時(shí)，我們可根據(jù)參考書（我的參考書為 4.32），而不是使用有限元解來計(jì)算應(yīng)力集中系數(shù)。參考書中有一個(gè)隱含假設(shè)：在第一個(gè)載荷工況中，載荷是均勻分布的。因此，即便載荷實(shí)際上只施加到一小塊邊界上，該例中的臨界距離仍與整個(gè)邊界尺寸都有關(guān)。

如果使用有限元方法（FEM）來求解問題，孔可以任意接近載荷。唯一的限制是，從物理的角度來看，載荷分布是明確定義的。不過，只要我們對(duì)重新分布做出假設(shè)，就會(huì)存在關(guān)于載荷分布的隱含假設(shè)，而這個(gè)假設(shè)可能與實(shí)際情況不同。

零力系與應(yīng)變能密度

我們?cè)谏衔闹薪忉屃嗽谔囟ǖ倪m當(dāng)距離之外，應(yīng)力大小，其大小與載荷大小無關(guān)。因此，在處理線彈性時(shí)，我們總是可以疊加載荷工況。當(dāng)證明圣維南原理時(shí)，很容易沿著這個(gè)思路總結(jié)出一個(gè)原則：由無合力或力矩的載荷系統(tǒng)引起的應(yīng)力在一定距離之外很小，該距離與載荷作用邊界的尺寸是同一數(shù)量級(jí)。

所以，我們將對(duì)兩個(gè)合力相同的載荷系統(tǒng)的差別所導(dǎo)致的應(yīng)力進(jìn)行研究。近代的大多數(shù)證明都以這類零力系的應(yīng)變能密度的衰減的估計(jì)值為基礎(chǔ)。

回到上面的問題，我們可以計(jì)算各個(gè)載荷工況的差別，借此對(duì)由應(yīng)力場(chǎng)的差別造成的應(yīng)力或應(yīng)變能密度的衰減現(xiàn)象進(jìn)行準(zhǔn)確的研究。

合力為零的載荷工況的應(yīng)變能密度的對(duì)數(shù)。

合力為零的載荷工況對(duì)應(yīng)的薄板應(yīng)變能密度。為了使能量?jī)H僅取決于與載荷的距離而變化，對(duì)垂直方向的能量進(jìn)行了積分。

應(yīng)變能密度的對(duì)數(shù)衰減率與同載荷作用邊界的距離或多或少呈線性關(guān)系。這實(shí)際上符合現(xiàn)代證明的預(yù)測(cè)——應(yīng)變能密度的指數(shù)衰減。我們還能清晰地看到圓孔是如何短暫降低衰減率的。

對(duì)薄壁結(jié)構(gòu)應(yīng)用圣維南原理

眾所周知，對(duì)于殼體、梁和桁架之類的薄壁結(jié)構(gòu)，我們不能按處理“結(jié)實(shí)”物體的方式來應(yīng)用圣維南原理。因?yàn)楸”诮Y(jié)構(gòu)內(nèi)的載荷路徑少得多，所以擾動(dòng)傳播的距離比想象中遠(yuǎn)。上文的圓孔案例也出現(xiàn)了這種現(xiàn)象，只是薄壁結(jié)構(gòu)更加顯著。

在本文中，我們選擇研究一個(gè)符合 IPE100 截面標(biāo)準(zhǔn)的梁。梁末端受到軸向應(yīng)力的作用，應(yīng)力大小在兩個(gè)橫截面方向均呈線性分布。

使用等值線和箭頭來表示載荷分布。

由于載荷具有對(duì)稱性，因此其合力為零，所有軸線周圍的力矩也為零。橫截面高 100 mm，如果圣維南原理的標(biāo)準(zhǔn)形式對(duì)其適用，那么在距離末端截面約 100 mm 的地方應(yīng)力應(yīng)該很小。

梁內(nèi)的有效應(yīng)力。紅色等值線表示低于施加的峰值應(yīng)力的 5% 的應(yīng)力。

事實(shí)證明，為了使應(yīng)力低于施加的峰值應(yīng)力的 5%，應(yīng)力必須沿梁移動(dòng)近一米的距離，而上翼緣和下翼緣需要通過薄腹板傳遞力矩來保持平衡，這就造成應(yīng)力重新分布的效率非常低。

如果你十分熟悉梁的非均勻扭轉(zhuǎn)理論，比如翹曲理論或弗拉索夫理論，就會(huì)意識(shí)到施加的載荷有很大的雙力矩。雙力矩是一個(gè)橫截面量，其物理大小等于力 X 長(zhǎng)度 2。

或許在此例中（只是我個(gè)人的推測(cè)），圣維南原理有效的條件不僅是力和力矩為零，還有雙力矩為零。這一點(diǎn)可以通過增加四個(gè)可抵消雙力矩的點(diǎn)載荷來實(shí)現(xiàn)。該分析的結(jié)果如下圖所示。

繪圖顯示了添加了四個(gè)點(diǎn)載荷，雙力矩變?yōu)榱愫蟮挠行?yīng)力。現(xiàn)在 5% 的應(yīng)力等值線十分靠近載荷作用邊界。

我們沒有特意選擇施加點(diǎn)載荷的最優(yōu)位置，點(diǎn)載荷產(chǎn)生了極大的（實(shí)際為奇異的）局部應(yīng)力。不過，應(yīng)力很快下降，超出 100 mm 左右后都小于 5%。5% 的下限仍然是針對(duì)所施加的分布載荷而言，并沒有根據(jù)新的局部應(yīng)力進(jìn)行調(diào)整。增加點(diǎn)載荷之后，應(yīng)變能密度的對(duì)數(shù)衰減率加快了兩倍。

有限元分析中的圣維南原理

很多情況下，你可以直觀地認(rèn)為圣維南原理適用于有限元離散化問題。在本文中，我們主要探討分布載荷和不相容網(wǎng)格。

分布載荷

雖然我們?cè)谟邢拊Ｐ椭袑?yīng)力設(shè)為連續(xù)的邊界載荷，但總要將應(yīng)力施加在網(wǎng)格節(jié)點(diǎn)上。如下方案例所示，根據(jù)虛功原理載荷分布到單元內(nèi)部節(jié)點(diǎn)。

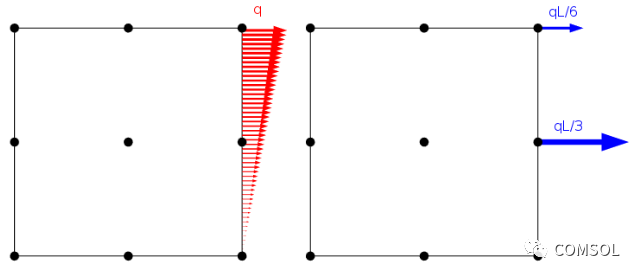
線性分布載荷以及如何將其施加在邊長(zhǎng)為 L 的二階拉格朗日單元節(jié)點(diǎn)上。

不過，只要合力和力矩相同，相同的節(jié)點(diǎn)載荷可以對(duì)應(yīng)無數(shù)種載荷分布。顯然，這類情況的有限元問題都擁有相同的解。不過，我們可以根據(jù)圣維南原理推斷，只要相距一定距離，這類載荷本質(zhì)上應(yīng)該產(chǎn)生相同的應(yīng)力場(chǎng)。

由于載荷重新分布的區(qū)域尺寸是基于單元面的，因此線性尺寸本質(zhì)上是結(jié)構(gòu)內(nèi)部的一個(gè)單元層。所以，單元最外層的解可能與實(shí)際載荷不符，內(nèi)部的解則相同。

舉個(gè)例子，我們對(duì)一塊矩形板施加了應(yīng)力呈指數(shù)分布的邊界載荷，并采用細(xì)化網(wǎng)格進(jìn)行了計(jì)算，應(yīng)力結(jié)果如下圖所示。

軸向應(yīng)力分布的等值線圖。

不出所料，受圣維南原理的影響，在離載荷作用邊一定距離的地方，應(yīng)力場(chǎng)重新分布成了純彎曲狀態(tài)。不過，這不是本次討論的核心。我們研究的是上方的應(yīng)力分布與使用粗化網(wǎng)格得到的應(yīng)力分布之間的差別。

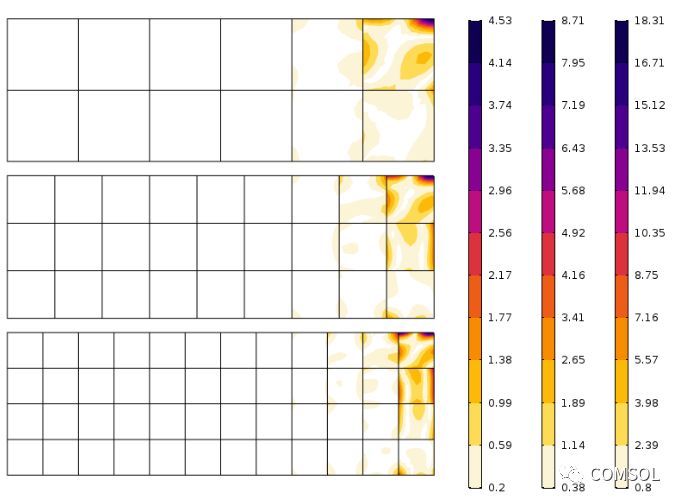
采用三種不同網(wǎng)格對(duì)應(yīng)的軸向應(yīng)力誤差。注意三者尺度不同。網(wǎng)格越細(xì)，誤差越小，這符合預(yù)期。

可以發(fā)現(xiàn)，經(jīng)過第一個(gè)單元層之后，誤差快速減少。圖中實(shí)際上是網(wǎng)格的收斂性和符合圣維南原理的應(yīng)力重新分布的共同效果。

不相容網(wǎng)格

當(dāng)兩個(gè)相互連接的單元的形函數(shù)不匹配時(shí)，會(huì)出現(xiàn)不相容網(wǎng)格。這類問題最常見于使用一致對(duì)和連續(xù)性條件來連接裝配的情況。為了舉例說明，我們選擇對(duì)一根包含故意不匹配的網(wǎng)格的直桿進(jìn)行研究。通過施加簡(jiǎn)單的載荷工況，比如單軸拉伸，我們就能研究由過渡導(dǎo)致的應(yīng)力擾動(dòng)。

不相容網(wǎng)格過渡處的軸向應(yīng)力。圖片使用了二階單元。

左右兩側(cè)的節(jié)點(diǎn)傳遞的力并不符合應(yīng)力不變的假設(shè)。這種情況也可以被看作局部載荷在等于單元大小的區(qū)域上進(jìn)行重新分布。根據(jù)圣維南原理，我們推斷在“單元大小”的距離之外，擾動(dòng)會(huì)逐漸消失。下面我們研究一下軸向網(wǎng)格細(xì)化后，將會(huì)出現(xiàn)什么情況。

應(yīng)力誤差大于 0.1% 的區(qū)域。在軸向上使用了三種不同的離散化。

結(jié)果證明，擾動(dòng)區(qū)域在垂直于過渡邊界的方向上不受離散化的影響。這與圣維南原理的推斷完全一致。

結(jié)束語

因?yàn)椴豢芍敿?xì)的載荷分布，所以如果不使用圣維南原理，很多結(jié)構(gòu)分析都難以進(jìn)行。

在形式上，原理只對(duì)線彈性材料有效。在實(shí)踐中，我們每天也會(huì)直覺地將其應(yīng)用于其他類型的仿真。舉例來說，如果“帶孔板”案例中的材料是彈塑性的，只要屈服應(yīng)力大于邊界應(yīng)力，且孔周圍只有彈性變形，我們就會(huì)預(yù)測(cè)兩個(gè)分布載荷生成相同的結(jié)果。不過，因?yàn)辄c(diǎn)載荷周圍的材料發(fā)生了屈服，所以點(diǎn)載荷總是生成不同的解。