邏輯回歸又稱邏輯回歸分析，是一種廣義的線性回歸分析模型，常用于數(shù)據(jù)挖掘、疾病自動診斷、經(jīng)濟預(yù)測等領(lǐng)域。

邏輯回歸是始于輸出結(jié)果為實際意義的連續(xù)值的線性回歸，因此與多重性線性回歸分析有很多的相同之處。

邏輯回歸模型

邏輯回歸是一種極易理解的模型，就相當(dāng)于y=f(x),表明自變量x與因變量y的關(guān)系。最常見的問題如：醫(yī)生治病時的望聞問切，之后判斷病人是否生病或生了什么病，其中的望聞問切就是獲取自變量x，即特征數(shù)據(jù)，判斷是否生病就相當(dāng)于獲取因變量y，及預(yù)測分類。

圖1 線性回歸示例

最簡單的回歸就是線性回歸，借用Andrew NG的講義來說，如圖1.a所示，x為數(shù)據(jù)點---腫瘤的大小，y為觀測值---是否有惡性腫瘤。通過構(gòu)建線性回歸模型，如hθ(x)所示，構(gòu)建線性回歸模型后，既可以根據(jù)腫瘤大小，預(yù)測是否為惡性腫瘤hθ(x)≥0.5為惡性，hθ(x)＜0.5為良性。

同時線性回歸的魯棒性很差，例如在圖1.b的數(shù)據(jù)集上建立回歸，因最右邊噪點的存在，使回歸模型在訓(xùn)練集上表現(xiàn)都很差。這主要是由于線性回歸在整個實數(shù)域內(nèi)敏感度一致，而分類范圍，需要在[0,1]。邏輯回歸就是一種減少預(yù)測范圍，將預(yù)測值限定為[0,1]間的一種回歸模型，其回歸方程與回歸曲線如圖2所示。邏輯曲線在z=0時，十分敏感，在z＞＞0或z＜＜0處，都不敏感，將預(yù)測值限定為(0,1)。

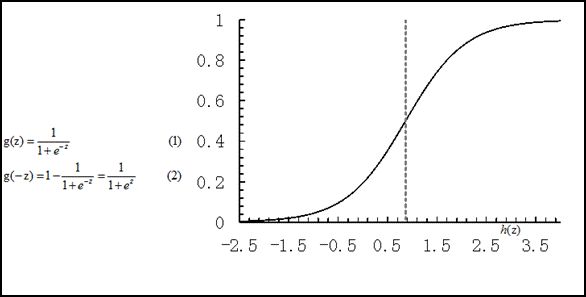
圖2 邏輯方程與邏輯曲線

邏輯回歸其實僅為在線性回歸的基礎(chǔ)上，套用了一個邏輯函數(shù)，但也就由于這個邏輯函數(shù)，邏輯回歸成為了機器學(xué)習(xí)領(lǐng)域一顆耀眼的明星，更是計算廣告學(xué)的核心，對于多元邏輯回歸，可用如下公式似和分類，其中公式(4)的變換，將在邏輯回歸模型參數(shù)估計時，化簡公式帶來很多益處，y={0,1}為分類結(jié)果。

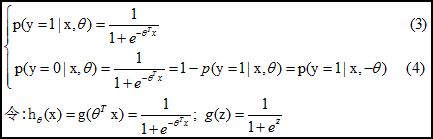
2. 判定邊界

為什么邏輯回歸能夠解決分類問題呢？我們可以用判定邊界來解釋，可以理解為是用對不同類別的數(shù)據(jù)分割的邊界，邊界的兩旁應(yīng)該是不同類別的數(shù)據(jù)。

從二維直角坐標系中，舉幾個例子，大概是如下這三種類型：

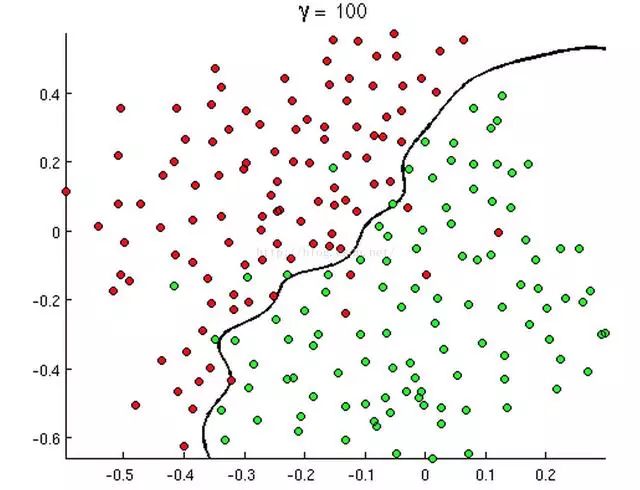
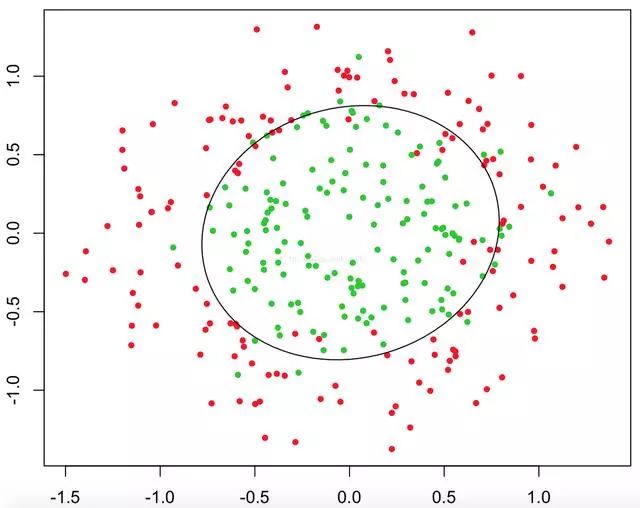
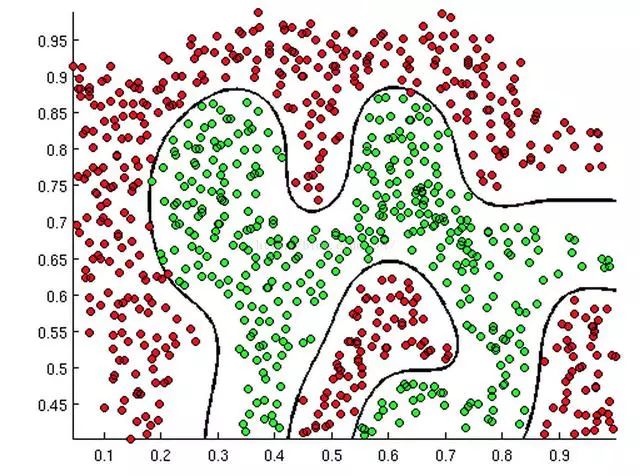
從上述三幅圖中，紅綠樣本點為不同類別的樣本，而我們劃出的線，不管是直線、圓或者是曲線，都能比較好地將圖中的兩類樣本分隔開，這就是我們所說的判定邊界，那么邏輯回歸是如何根據(jù)樣本點來獲得這些判定邊界的呢？

我們依舊借用Andrew NG教授的課程中部分例子來講述這個問題。

回到sigmoid函數(shù)，我們發(fā)現(xiàn)，當(dāng)g(z)≥0.5時, z≥0;對于hθ(x)=g(θTX)≥0.5, 則θTX≥0, 此時意味著預(yù)估y=1;反之，當(dāng)預(yù)測y = 0時，θTX<0; 所以我們認為θTX =0是一個決策邊界，當(dāng)它大于0或小于0時，邏輯回歸模型分別預(yù)測不同的分類結(jié)果。先看第一個例子hθ(x)=g(θ0+θ1X1+θ2X2)，其中θ0 ,θ1 ,θ2分別取-3, 1, 1。則當(dāng)?3+X1+X2≥0時, y = 1; 則X1+X2=3是一個決策邊界，圖形表示如下，剛好把圖上的兩類點區(qū)分開來：

例1只是一個線性的決策邊界，當(dāng)hθ(x)更復(fù)雜的時候，我們可以得到非線性的決策邊界，例如：

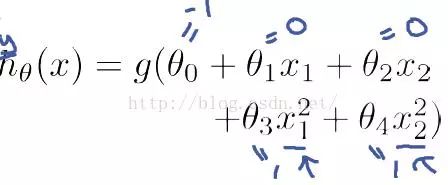
這時當(dāng)x12+x22≥1時，我們判定y=1，這時的決策邊界是一個圓形，如下圖所示：

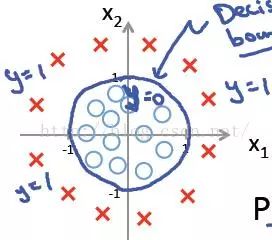
所以我們發(fā)現(xiàn)，理論上說，只要我們的hθ(x)設(shè)計足夠合理，準確的說是g(θTx)中θTx足夠復(fù)雜，我們能在不同的情形下，擬合出不同的判定邊界，從而把不同的樣本點分隔開來。

直觀地在二維空間理解邏輯回歸，是singmoid函數(shù)的特征，使得判定的閾值能夠映射為平面的一條判定邊界，當(dāng)然隨著特征的復(fù)雜化，判定邊界可能是多種多樣的樣貌，但是它能夠較好地把兩類樣本點分隔開，解決分類問題。