期望值是大量試驗之后隨機變量的平均值。隨機變量將數值映射到試驗的每個可能的結果。我們可以計算離散隨機變量的期望值——潛在的結果數目是可數的——每項是一個隨機變量的可能值,乘以該結果的概率,最后累加。例如,如果我們的隨機變量是投擲一個均勻的3面骰所得的數字,那么期望值將是(1 * 1/3) + (2 * 1/3) + (3 * 1/3) = 2。
如果我們假設試驗是一個游戲,那么隨機變量映射游戲結果至收益,因而期望值表示期望的游戲平均收益。由于期望值是實數,它通常分為負值、中性值、正值。在日常生活場景中,期望值為負、期望值為中性、期望值為正的游戲都很常見,所以期望值提供了一個簡單的決策推斷法。
下面我將舉例說明每種類型的游戲,我會使用3個類似的扔硬幣的例子,具體來說,每個場景中的隨機變量將是扔一次硬幣后的期望收益。假設所有情形下硬幣是均質的,所以得到正面和反面的概率是一樣的(1/2)。
中性期望值游戲
你扔一枚均質硬幣。每次扔到正面,你損失1美元,每次扔到反面,你獲得1美元。
這一場景下的期望值為(-1 * 1/2) + (1 * 1/2) = 0。因此,由于硬幣是均質的,損失和收益相等,隨著時間的推移,你可以期望既不贏錢也不輸錢。在這樣的游戲中,盡管沒有理由進行這一游戲,也沒有理由不進行。因此,這類游戲是一種理想的簡單娛樂形式,比如剪刀石頭布,隨機選擇是期望值為0的最優策略。
正期望值游戲
你扔一枚均質硬幣。每次扔到正面,你損失1美元,每次扔到反面,你獲得2美元。
這一場景下的期望值為(-1 * 1/2) + (2 * 1/2) = 1/2。由于正面和反面出現的概率一樣,扔到反面時較大的收益超過了扔到正面時的損失。在這樣的游戲中,隨著時間的推移,你可以期望得到更多的錢,所以你應該玩這類游戲。這類場景出現在許多現實生活的決策中,例如投資股票市場(總體而言,隨著時間的推移,市場的走勢是向上的),為考試而學習(更高的GPA收益超過了損失的一些時間),準備面試(得到更好的工作的收益超過了損失的幾周時間)。
負期望值游戲
你扔一枚均質硬幣。每次扔到正面,你損失1美元,每次扔到反面,你獲得1美元。此外,不管結果如何,每扔一次硬幣,你都需要支付1美分的費用。
這一場景下的期望值為(-1.01 * 1/2) + (.99 * 1/2) = -0.01。因此,盡管硬幣本身是均質的,損失數額也等于收益數額,恒定的費用導致這一游戲變為負值游戲。在這樣的游戲中,你可以期望隨著時間的推移而虧錢。所以你不應該玩這類游戲。這在很多賭博平臺上很常見,賭場提供初始為中性的游戲,但通過收費破壞了游戲的中性(俗話說:“賭場只賺不賠。”)。
結語
基于期望值進行決策是一個判定參與某項活動是否在經濟學上合理的簡單方式。當然,除了純粹的經濟回報,還有其他衡量可用性的方式,所以期望為正并不是一個傻瓜式的決策工具。此外,別忘了期望值需要大量重復的試驗才能起效,因此對于特定事件(其中的一些概率極其罕見)而言,期望值可能提供了扭曲的視角。例如,考慮彩票得獎。盡管彩票有可能有機會是正期望值(譯者注:比如由于前面好幾期無人得頭獎,獎池累積金額很高,國內福利彩票獎池設有上限,期望值不可能為正),但你在你有限的人生中實際實現這一期望值的概率極低,所以買彩票并不值。
-
隨機變量
+關注
關注
0文章
11瀏覽量
6467
原文標題:什么是期望值?
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
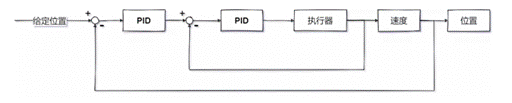
什么是串級PID? 簡單PID和串級PID的優劣對比




 通過簡單的例子介紹期望值
通過簡單的例子介紹期望值










評論